statusx.php?runidx=11338119

题目：

【题目描述】

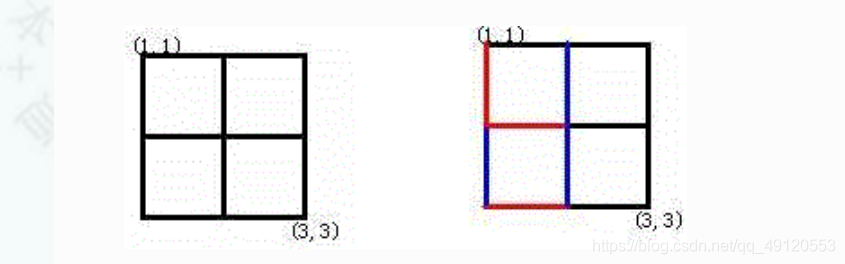
Alice和Bob玩了一个古老的游戏：首先画一个n × n的点阵（下图n = 3）

接着，他们两个轮流在相邻的点之间画上红边和蓝边：

直到围成一个封闭的圈（面积不必为1）为止，“封圈”的那个人就是赢家。因为棋盘实在是太大了(n ≤ 200)，他们的游戏实在是太长了！他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序，帮助他们计算他们是否结束了游戏？

【输入】

输入数据第一行为两个整数n和m。m表示一共画了m条线。以后m行，每行首先有两个数字(x, y)，代表了画线的起点坐标，接着用空格隔开一个字符，假如字符是"D "，则是向下连一条边，如果是"R "就是向右连一条边。输入数据不会有重复的边且保证正确。

【输出】

输出一行：在第几步的时候结束。假如m步之后也没有结束，则输出一行“draw”。

【输入样例】
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
【输出样例】
4

思路：

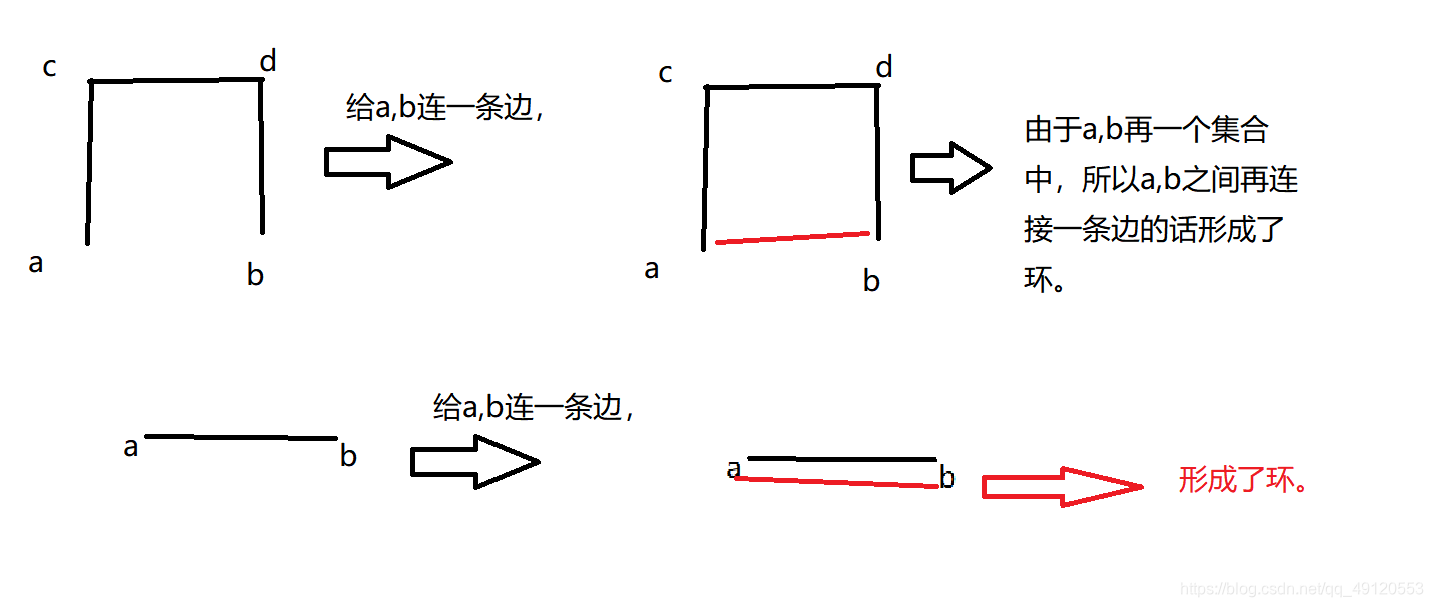
判断是否为连接一条边后组成环的话，可以使用并查集的方式，判断所连接的两个点是否已经再一个集合中了，如果两个点已经在一个集合中了，再用一条边连接这个两个点的话，必定会组成一个环，?

?所以判断某两个点连接后是否会形成环，只要判断这两个点是否再同一集合中就可以了。而判断某两个点是否再同一集合中，使用并查集即可。

还需要注意一点：

并查集经常处理一维的情况，而此题为二维，但是我们可以将其从二维转为一维。

而一个矩形坐标二维的形式转为一维有一个常用的方式。?

一个 n 行 m 列的矩形：有一个坐标为x1,y1的点，转为一维为：

x1 * m + y1? （此为左上角为（0，0），转为的一维也是0开头。）

或者 ( (x1 - 1) * m + y1? ?)? (此为左上角为(1,1)开头)

代码实现：

/* 并查集 时常 以 一维的方式进行计算，所以此题我们将二维转为一维 */
# include <iostream>
# include <stdio.h>
using namespace std;
const int N = 40010;

int p[N];

int n,m;

int findf(int i)
{
    if(p[i] != i)
    {
        p[i] = findf(p[i]);
    }
    return p[i];
}

int get(int x , int y)
{
    return x * (n - 1) + y;
}

int main()
{
    scanf("%d %d",&n,&m);
    for(int i  = 1 ; i <= n * n; i++)
    {
        p[i] = i;
    }
    int flag = -1;
    for(int i = 1 ; i <= m ; i++)
    {
        int x,y;
        char ch;
        cin >>x >>y >>ch;
        int a = get(x ,y);
        int b;
        if(ch == 'D')
        {
            b = get(x + 1, y);
        }
        else
        {
            b = get(x , y + 1);
        }
        if(flag == - 1 &&findf(a) == findf(b))
        {
            flag = i;
        }
        p[findf(a)] = findf(b);
    }
    if(flag != -1)
    {
        printf("%d\n",flag);
    }
    else
    {
        printf("draw\n");
    }
    return 0;
}