堆的概念
物理与逻辑结构的转换
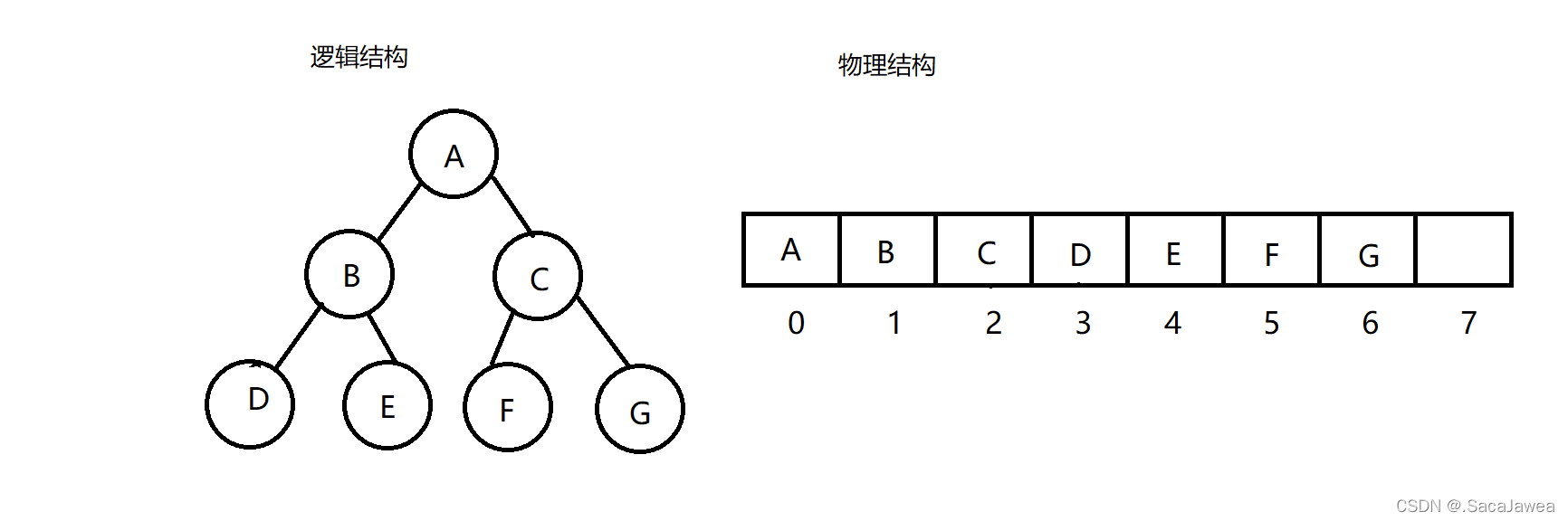
图片上的二叉树是一颗完全二叉树,并且它还是一颗满二叉树。而数组能完美的表示像完全二叉树这样的结构。
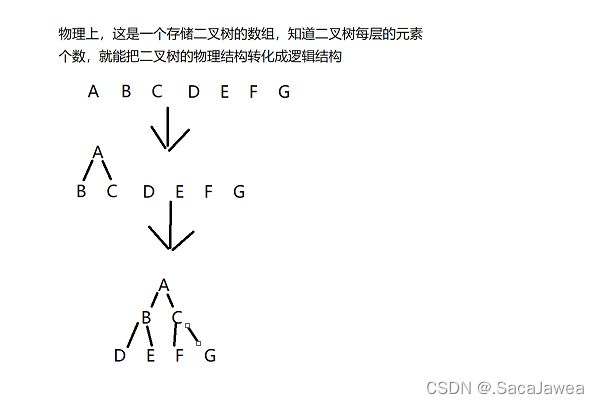
从根节点开始,根节点为第一层,从上往下,从左往右,将数据存储到数组中。二叉树第i层的元素个数为2的(i - 1)次方,知道每层二叉树的元素个数,就能把数组中的数据转化为二叉树的形式。
第一层二叉树有2的(1 - 1)次方,1个元素,一层一层地将数组转化成二叉树
堆的性质
1.堆总是一颗完全二叉树
2.堆的节点总是不大于或不小于其父节点
若一颗二叉树根节点的值小于其孩子节点,并且该树满足堆的性质,该树称作小堆。反之根节点大于其孩子节点,该树称作大堆。
堆的实现
堆在物理上是一个数组,虽然在逻辑上不是顺序表,但可以用顺序表的结构表示堆。
堆结构的声明
typedef int HDataType;//HDataType表示堆中存储的数据类型
typedef struct Heap
{
HDataType* data; //像顺序表一样,堆结构中有一个data指针指向存储数据的数组
size_t size; //size表示当前堆的数据个数
size_t capacity; //capacity表示堆的容量
}Heap;
堆的基础接口
void HeapInit(Heap* php); //堆的初始化
void HeapDestory(Heap* php); //堆的销毁
void HeapPush(Heap* php, HDataType(Heap* php);//插入数据到堆中
void HeapPop(Heap* php); //堆顶数据的删除
HDataType HeapTop(Heap* php); //堆顶元素的返回
bool HeapEmpty(Heap* php); //堆的判空
size_t HeapSize(Heap* php); //堆元素个数的返回
堆的初始化与销毁
//对堆的成员赋初值
void HeapInit(Heap* php)
{
assert(php);
php->size = 0;
php->capacity = 0;
php->data = NULL;
}
//将malloc申请的空间释放,并且对堆的容量与元素个数置0
void HeapDestory(Heap* php)
{
assert(php);
free(php->data);
php->capacity = 0;
php->data = NULL;
}
堆的Push与Pop

假设往图片中的小堆插入一个9,将9插入数组的最后一位,插入数据时要先检查数组的空间是否足够存储,检查扩容。找到9的父节点,比较其与父节点的大小,如果父节点大于9,则把父节点与9交换,交换后再与交换后的父节点比较,判断是否要再次交换。最坏的情况就是交换到根节点
父节点与子节点的下标关系,(子节点下标 - 1) / 2得到父节点的下标
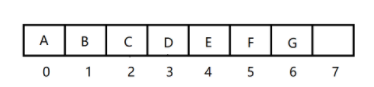
C的下标为2,- 1 再 / 2得到0,说明A是C的父节点,B的下标是1,-1 再 /2得到0,说明A是B的父节点。

交换节点时,只会影响到插入节点的祖先节点。
//先浏览HeapPush接口
//交换接口
void Swap(HDataType* pa, HDataType* pb)
{
HDataType tmp = *pa;
*pa = *pb;
*pb = tmp;
}
//向上调整接口
void AdjustUp(Heap* php, size_t child)
{
size_t parent = (child - 1) / 2;
while(parent > 0)//只要其父节点大于0,循环继续
{
//如果孩子节点小于父亲节点,交换
if (php>data[child] < php->data[parent])
{
Swap(&php>data[child], &php->data[parent]);
child = parent;
parent = (child - 1 ) / 2;
}
else//父亲节点大于孩子节点,满足堆的性质,跳出循环
{
break;
}
}
}
//堆的Push接口
void HeapPush(Heap* php, HDataType x)
{
assert(php);
//检查扩容
if (php->size == php->capacity)
{
//如果数组满了,需要扩容。新的容量根据原来容量是否为0来判断,如果是0,新容量为4,不是0,新容量为原来的两倍
size_t newCapacity = (php->capacity == 0) ? (4 : php->capacity) * 2;
//将原来空间扩容,用tmp接收新开辟空间的地址
HDataTpye* tmp = (HDataTpye*)realloc(php->data,sizeof(HDataTpye) * newCapacity);
if (!tmp)
{
printf("realloc fail\n");//若开辟空间失败,if条件成立,需要结束程序
exit(-1);
}
php->data = tmp;//若开辟成功,将开辟好的空间地址给data
php->capacity = newCapacity;
}
php->data[php->size] = x;
php->size++;
//插入元素后要将元素像上调整,使其始终是一个堆
AdjustUp(php, php->size - 1);
}
删除堆顶元素,不能将后面的数据往前覆盖,删掉第一个节点,这样操作会打乱堆中元素的父子关系

如图片中的小堆,逻辑上的表示如下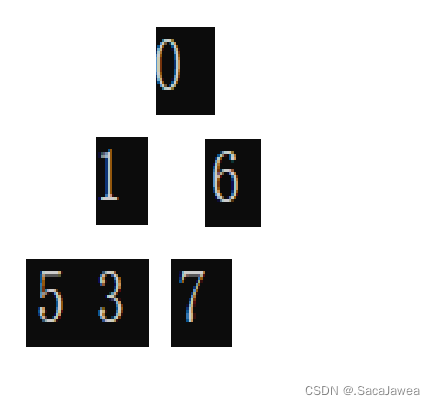
将后面的元素删除,得到的小堆是
3的父节点大于3,很明显不满足小堆的性质。所以删除堆顶元素得用其他算法。
将堆顶元素与数组的最后一个元素交换,再将堆的size减1,此时的堆的堆顶不满足堆的性质,将堆顶向下调整:找到两个子节点中小的那个,将两者交换,再找交换后两子节点中小的那个,再交换,知道子节点中小的那个大于自身。
以上作为一个循环,当其没有子节点时,说明到了叶节点,循环结束
细节:两个子节点中,可能只有一个左子节点,所以要判断右节点是否存在,否则会出现越界访问
//向下调整接口
void AdjustDown(Heap* php, size_t size, size_t root)
{
size_t parent = root;//父节点
size_t child = root * 2 + 1;//父节点的左子节点
while (child < size)//若父节点的子节点下标在数组范围内,循环继续
{
//假设左节点是两节点中最小的,交换时只要交换parent与child,但要判断右节点的大小
//若父节点的右节点存在,并且右节点小于左节点,将child换为右节点
if (php->data[child + 1] && \
php->data[child + 1] < php->data[child])
{
child++;//右节点的下标比左节点大1
}
if (php->data[parent] > php->data[child])//父节点大于子节点,交换
{
Swap(&php->data[parent], &php->data[child]);
//父节点与子节点的更新
parent = child;
child = parnet * 2 + 1;
}
else//父节点小于子节点,满足堆的性质,跳出循环
{
break;
}
}
}
//堆的Pop接口
void HeapPop(Heap* php)
{
assert(php);
assert(php->size > 0);//堆中的元素数不能少于1
//将数组中的第一个元素与最后一个元素交换
Swap(&php->data[0], &php->data[php->size - 1]);
AdjustDown(php->data, php->size, 0);//将堆顶元素向下调整
}
堆的判空,堆顶元素的返回与长度的返回
三个接口较简单
//判空接口
bool HeapEmpty(Heap* php)
{
assert(php);
return (php->size == 0);
}
//堆顶元素返回接口
HDataTpye HeapTup(Heap* php)
{
assert(php);
assert(php->size > 0);
return php->data[0];
}
//堆的长度返回
HDataType HeapSize(Heap* php)
{
assert(php);
return php->size;
}
堆排序
堆顶元素总是堆中最小元素,若要将数组以升序的顺序排序,每次只要取出堆顶元素,取出后,调用堆的Pop接口,Pop数据,此时Pop会调整堆中元素的顺序,使得堆顶元素是最小的数,再取堆顶数据,再调Pop接口…
//将arr数组的数据堆排序,size是数组长度
void HeapSort(HDataType* arr, size_t size)
{
Heap hp = { 0 };//定义一个堆结构hp
HeapInit(&hp);
for (int i = 0; i < size; i++)
{
HeapPush(&hp, arr[i]);//将arr中的数据Push到堆中
}
for (int i = 0; i < size; i++)
{
arr[i] = HeapTop(&hp);//将堆顶元素(最小的数)存到arr数组中
HeapPop(&hp);//删除堆顶元素
}
}
运行结果如下
