一、前K短路径含义
? ? ? ? 各个高校的数据结构或算法的教材普遍会介绍求解最短路径的问题。
? ? ? ? 最短路径问题一般分为两种:
? ? ? ? ? ? ? ? 单源最短路径,即指定点到其余个点的路径;
? ? ? ? ? ? ? ? 两对顶点之间的最短路径。
? ? ? ? 狭义的最短路径问题只能求解出一条最短的路径,但是很多时候我们需要知道第二短,第三短......等次优解、次次优解问题,而本文介绍的Yen算法就是解决此类问题的一种算法。
? ? ? ? ?Yen算法是由发明者的名字命名的,相信阅读了本文的同学应该也查阅了其他文章,了解到Yen算法的来历。其他大牛写的文章普遍都介绍了A*算法、启发式函数等等,不过本人只是一个普通的大一学生,我只会用比较粗浅的方式向你介绍这个算法,我给出的实现方式以及各种结构也是我自己构造的,所以如果你是一个和我一样的大学生的话,本文可能更适合你来理解Yen算法。
二、了解算法前所必须了解的一些定义
????????
我用此图来说明一下必要的概念。
? ? ? ? 1、偏离点:路径P3相对于P1的偏离点为 2
? ? ? ? 2、偏离路径:P3相对于P1的偏离路径为 2 4 5
三、阐述Yen算法
????????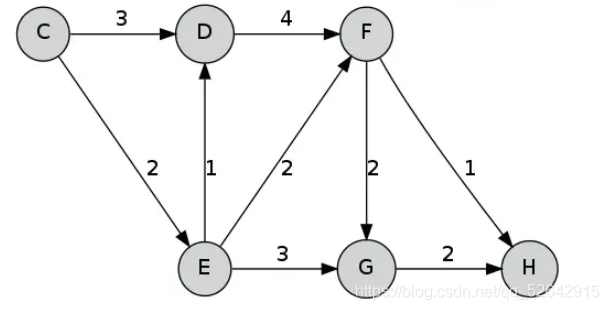
对上图编号,规定 C D F E G H对应的编号分别为1、2 、3、4、5、6。
假设我们要求C点到H点的k短路径,并且假设我们已经得到了C H之间的最短路径P1。
Yen算法的思想就是在最短路径P1上产生偏离路径,依次来求得k短路径。
接下来我按照Yen的思想来用P1求得P2。
不难发现图中P1路径应为:C E F H。
Yen算法要求我们将P1路径上除终点外的每一点都依次看作偏离点来求解,
先将点C看作偏离点,那么如果我们知道了从C点到H点的最短路径(当然,此路径不能与P1重合),那么此路径就为C点作为偏离点得到的路径,我设为pk1。
接下来将E点看作偏离点,同样的,如果我们知道了从E点到H点的最短路径(不与已有的重合),
那么由E点作为偏离点得到的路径就是由E点的偏离路径+CE这条边组成的路径,我设为pk2.
然后将F点作为偏离点,假设得到了F点到H点的最短不重合路径,那么由F点作为偏离点得到的路径即为F点的偏离路径+CEF,我设为pk3.
于是我们得到了pk1 pk2 pk3,那么我只要从中选出一条总权值最小的路径,它就是仅次于P1的第二短路径。我将其称为P2。
那么要想求解P3,只需将P2作为原来的P1带入到上述描述中即可(即将P2路径上除终点外的路径依次作为偏离点求解)。求解P4、P5......亦同理。
不过,在上述的描述中我们还遗留了许多问题:
? ? ? ? 1.P1如何求?
? ? ? ? 2.每个偏离点到终点的不重合最短路径应该如何求?
? ? ? ? 3.在求解P3、P4、P5......与求P2时有哪些要注意的细节?
对于1:
? ? ? ? P1直接调用Dijkstra算法即可得
对于2:
? ? ? ? 任然是调用Dijkstra算法,不过我们要对Dijkstra算法做一些修改。修改体现在对path和dist得初始化上。由上述描述我们知道,每一次求解偏离点到终点的路径时都是有一些边不能用的,那么我们只需要在初始化把这些边从我们的图上给”删除掉“即可。
? ? ? ? 以C点作为偏离点时为例,我们只需把Path[顶点E的编号]=-1;Dist[顶点E的编号】=MAX;即可。
对于3:
? ? ? ? 事实上,问题3需要注意的细节任然在与“不能使用的边”。
对于由P1求解P2的过程,我们只需考虑偏离路径不与P1重复即可,但事实上当我们由Pk求解Pk+1时,我们的已求解的路径已经有了K条,所以再求解Pk+1时要与之前的K调皆不重合。
四、代码
1、我自己定义的一些结构
class Path//用于描述路径的类
{
public:
int VerList[Max];
int Alleweight;
int NodeNum;
int Dist[Max];
}
class VectorForPath//用于存储已选路径和候选路径的类,我是用的小根堆存储
{
public:
Path paths[Max];//下标取从1 到 n 即 Num为元素个数亦为数组下标
int Num = 0;
void Add(Path p);//入队
void siftForAdd(int num);//为入队的调整函数
Path SelectAndDelete();//出队
void siftForDelete(int num);
Path GetTop()
{
return paths[1];
}
};
2.有关Yen
我先写出我构建Yen算法的过程,接着再给出代码。
首先,对于求得两个顶点直接K短路径的函数而言,我们希望的输出有:前K短路径的集合
而必要的输入为:K短路径的参数K、指定的两个顶点 vBegin vEnd
故有void Yen(int vBegin,int vEnd,int K,VectorForPath& VFP);
//Yen算法
void Yen(int vBegin, int vEnd,VectorForPath& VFP,int K);//输出是k短路径的集合
bool Yen_initial(int vBeign, int vEnd, VectorForPath& VFP);//对Yen进行初始化,返回值表示了指点两点间是否存在一条路径,若无则直接结束算法
bool myDijkstra(int vID,int vEnd, VectorForPath VFP,Path& ptemp,Path Pk);
//自定义的Dijkstra
void InitialFormyDijkstra(int path[], int dist[], int vID, VectorForPath VFP,Path Pk);
//为满足Yen的要求,对Dijkstra做特殊的初始化
void dealDijkstra(int path[], int dist[],Path& p,int vEnd,Path Pk);
//对由Dijkstra算法得到的参数Path与Dist进行转化,将其转化为我自己构造的结构 Path里
void SearchUnusedEdge(VectorForPath VFP, int arr[], int& num,int vID,Path Pk);
//用于找到不能使用的边的函数
bool ifEgzist(Path p, VectorForPath VFP_Wait);
//用于新得到的候选路径是否与侯选路径集合里的路径重合
接下来给出各个函数具体实现
? ? ? ? (1)、Yen
//Yen
void GraphAdjMatrix::Yen(int vBegin, int vEnd, VectorForPath& VFP, int K)
{
bool BOOL= Yen_initial(vBegin, vEnd, VFP);
if (BOOL == false)return;
Path p = VFP.GetTop();
VectorForPath VFP_Wait;//VFP 是用堆存储的,其数组下标从1开始
int k = 2;
while (k <= K)
{
for (int i = 0; i < p.NodeNum-1; i++)
{
Path ptemp = p;
bool ifHasPath =myDijkstra(p.VerList[i],vEnd,VFP,ptemp,p);
bool s = ifEgzist(ptemp, VFP_Wait);
if (ifHasPath&&!ifEgzist(ptemp,VFP_Wait))VFP_Wait.Add(ptemp);
}
if (VFP_Wait.Num == 0)return;
p = VFP_Wait.SelectAndDelete();
VFP.Add(p);
k++;
}
}
(2)、Yen_initial
bool GraphAdjMatrix::Yen_initial(int vBegin, int vEnd, VectorForPath& VFP)
{
Path p;
bool ifHasPath=myDijkstra(vBegin,vEnd,VFP,p,p);
if (ifHasPath)
{
// dealDijkstra(path, dist, p, vEnd);
VFP.Add(p);
return true;
}
else return false;
}
(3)、myDijkstra
bool GraphAdjMatrix::myDijkstra(int vID,int vEnd,VectorForPath VFP,Path& p,Path Pk)
{
/*
1、vID为第一个选定点 初始化 path dist
2、选取dist最小的一个边 将此边的邻接点变为已解点
3、考虑新加入点的影响,对dist与path进行修改
4、重复2、3
//以上为原dijkstra算法
而为满足Yen算法的要求 应做如下修改:
考虑到Yen算法求解偏离点到汇点的最短路径时是建立在之前的偏离路径基础上的,故而对部分偏离点来说,可能会存在不能选的边
在原有的初始化过后,要对path 与 dist 进行特殊的修改,把不能选的边从dist中把权值变为无穷大,从path中的前驱从vID变为-1
而后再从剩余的dist中选取最小的一个边。将此边的邻接点变为已解顶点
然后考虑新加入点的影响,对dist与path进行修改
重复上述两句话,如此就得到了在Yen算法限制下的最短偏离路径
不过实际上,上述的改变了的dijsktra算法只是求解出了一个偏离点的从偏离点到汇点的最短路径
将此路径与从源点到偏离点的路径拼接起来方得到了点i作为偏离点是的路径p,将p放入侯选路径集合里
当每个偏离点都进行完上述操作后,那么我们从侯选路径集合里找出Alleweight最小的一个路径,作为Pk短路径
当然,要判断此次得到是否已经与候选集和了的重合
*/
//Part One-----initial
int path[Max];
int dist[Max];
InitialFormyDijkstra(path, dist, vID, VFP,Pk); //满足Yen的初始化path dist
for (int i = 0; i < p.NodeNum; i++)
{
if (p.VerList[i] != vID)
solved[i] = true;
else break;
}
dist[vID - 1] = 0;
for (int i = 0; i < VerNum - 1; i++)
{
int minID = minSelect(dist);
if (minID == -1)break;
DP_change(path, dist, minID);
}
Path ptemp;
dealDijkstra(path, dist, ptemp,vEnd,Pk);
//这时的dist是偏离点到其余各点的最短路径
//Pk 是当前轮次的主路径,当求P1时 Pk为None
//求p1时 p1.dist被赋值为
//经过deal ptemp:
/*
1、verList 里保存着偏离点到vEnd的路径
2、eWeigth 是偏离点到vEnd的总权值
3、ptemp.dist 里保存着偏离点到其余各点的最短距离
*/
if (ptemp.VerList[ptemp.NodeNum - 1] != vEnd)return false;
for (int i = 0; i < VerNum; i++)
{
p.Dist[i] = ptemp.Dist[i];
}
//把源点到偏离点路径与偏离点到汇点路径拼接起来
//我想要返回的p是一个候选路径
if (p.NodeNum != 0)
{
int Pnum;
for (Pnum = 0; Pnum < p.NodeNum; Pnum++)
{
if (Pk.VerList[Pnum] == ptemp.VerList[0])break;
}
p.Alleweight = Pk.Dist[vID-1]+ ptemp.Alleweight;
int tempnum = p.NodeNum;
p.NodeNum = Pnum+ ptemp.NodeNum;
tempnum = (p.NodeNum > tempnum) ? p.NodeNum : tempnum;
int j;
for (j = 0; j < ptemp.NodeNum; Pnum++,j++)
{
p.VerList[Pnum] = ptemp.VerList[j];
}
}
else
{
p = ptemp;
}
//TODO
if (p.VerList[p.NodeNum - 1] != vEnd)return false;
else return true;
}(4)InitialFormyDijkstra
void GraphAdjMatrix::InitialFormyDijkstra(int path[], int dist[], int vID, VectorForPath VFP,Path Pk)
{
//Part one normalInitial
for (int i = 0; i < VerNum; i++)solved[i] = false;
solved[vID - 1] = true;
for (int i = 0; i < VerNum; i++)
{
if (AdjMatrix[vID - 1][i] != 0)
{
path[i] = vID;
dist[i] = AdjMatrix[vID - 1][i];
}
else
{
path[i] = -1;
dist[i] = MAX;
}
}
dist[vID - 1] = 0;
//Part two ForYen
int arr[Max]; int num = 0;
SearchUnusedEdge(VFP, arr, num,vID,Pk);//arr 里保存的是与vID相连的且不能使用的边的邻接点
for (int i = 0; i < num; i++)
{
path[arr[i] - 1] = -1;
dist[arr[i] - 1] = MAX;
}
}
(5)、dealDijkstra
void GraphAdjMatrix::dealDijkstra(int path[], int dist[], Path& p,int vEnd,Path Pk)
{
//把path 与 dist 转化为 p里的verlist 、alleweight 、 nodenum
Stackint s;
int temp = vEnd;
if(path[vEnd-1]!=-1) s.pushStack(vEnd);
while (path[temp-1] != -1)
{
s.pushStack(path[temp - 1]);
temp = path[temp - 1];
}
int num = 0;
while (!s.StackEmpty())
{
s.popStack(p.VerList[num++]);
}
p.NodeNum = num;
p.Alleweight = dist[vEnd - 1];
int flag = 0;
if (Pk.NodeNum != 0)
{
for (int i = 0; i < VerNum; i++)
{
p.Dist[i] = Pk.Dist[i];
}
int vID = p.VerList[0];
for (int i = 0; i < p.NodeNum; i++)
{
int vIDtemp = p.VerList[i];
p.Dist[vIDtemp - 1] = dist[vIDtemp - 1] + Pk.Dist[vID - 1];
}
}
else
{
for (int i = 0; i < VerNum; i++)
{
p.Dist[i] = dist[i];
}
}
}
(6)、searchUnusedEdge
void GraphAdjMatrix::SearchUnusedEdge(VectorForPath VFP, int arr[], int& num,int vID,Path Pk)
{
for (int i = 1; i <= VFP.Num; i++)
{
Path p = VFP.paths[i];
for (int j = 0; j < p.NodeNum; j++)
{
if (Pk.VerList[j] != p.VerList[j])break;
if (p.VerList[j] == vID)
{
if (j + 1 < p.NodeNum)
{
arr[num++] = p.VerList[j + 1];
}
break;
}
}
}
}
(7)ifEgzist
bool GraphAdjMatrix::ifEgzist(Path p, VectorForPath VFP_Wait)
{
for (int i = 1; i <= VFP_Wait.Num; i++)
{
if (p == VFP_Wait.paths[i])return true;
}
return false;
}
------------------------------------------------------------------------------------------------------------
第一次写博客,有一说一,真难写,而且写的真的烂。。。。
很多东西我以为自己理解的很好了但是真的很难表述出来。
这篇文章远远不能满足教学的要求。
再接再厉。