数组是各种计算机语言中经常使用到的重要数据结构，一般的说：在内存中申请一片连续地址的存储空间、存储这些数、就称为数组。
在C语言中，申请连续的存储空间是很容易的事情，但难在多维数组的组织、以及数组数据的压缩上，以下的介绍就是给大家说明如何组织多维空间的数组。
1 C语言的可变参数函数
在C语言中，大多教材所介绍的内容中，一个函数的参数个数是确定的，比如：
#include<stdio.h>
double BoxVolume(double a,double b,double c)
{
return a*b*c;
}
main()
{
double x,y,z;
X=1;y=2;z=3;
prinrf(“%f\n”,BoxVolume(x,y,z));
}
函数BoxVolume()有三个参数，在实际编程中，调用这个函数不得少于三个参数、也不得多于三个参数。在main()中的调用中就是这样。
但可变参数的函数是我们在C语言中也见过的，比如：
printf(“%d %d\n”,a,b); //有三个参数。
printf(“%d %d %d\n”,a,b,c); //有四个参数。
同样，scanf()也是个可变参数函数，调用该函数、参数个数是不确定的。这说明C语言函数个数可以是不确定的。说明一个可变参数函数，把可变参数定义为：
…
就是三个小数点。如：
Fun(char ch,int m,…)
{
函数体
}
其中char ch,int m是固定参数部分，而…则代表可变参数部分。
C语言中，可变参数的数据读取，是由可变参数变量来完成的，这是个不常见的数据类型，说明方法是：
va_list 可变参数变量名称;
比如：
va_list ap;
说明了一个可变参数变量ap，要读这些参数，首先要说明从哪个参数开始读，如果我们打算从参数m后读，就是：
va_start(ap,m);
这样就能用下面的语句读到参数m以后各个参数的值，假如都是整数的话就是：
n=va_arg(ap, int);
一个完整的范例如下：
#include <stdarg.h>
#include <stdio.h>
void vFun(char ch,int m, ...)
{
va_list ap;
int n,j;
//读固定参数部分
printf("%c\n",ch);
//从参数m后读可变参数部分
va_start(ap,m);
for (j=0;j<m;j++)
{
n=va_arg(ap, int);
printf("%d %d\n", m, n);
}
va_end(ap);
return;
}
main()
{
vFun('x',5,1,2,3,4,5);
}
这个测试程序调用可变参数函数vFun()，使用的是：
vFun('x',5,1,2,3,4,5);
它的意思是说参数m为5，然后读后面的数字。当然用：
vFun('a',8,1,2,3,4,5,6,7,8);
调用这个函数也可以，很正确。你可以随意设置参数的个数。
这个程序看明白了，再读教材P98的数组ADT就可以了。
2 数组的存储方式
首先要确定计算机的内存，绝大多数是线性结构，也就是地址是一维的，但我们的数组，却可能是N维的，为解决这个，首先我们先看一个下面的分析。
对一维数组，直接申请内存、逐个存储数据就是；
对二维数组，则按先行后列保存数据，比如：
所谓先行，就是先取第一行1、2、3，按一维数组保存，再取4、5、6，继续保存，再取7、8、9，这样，这个数组在内存中就是按：
1、2、3、4、5、6、7、8、9
这样的次序来保存了。如果申请内存的开始地址是100，每个数据1字节，那么上述数据在内存中存储的情况就是：
如果取该数组A[1][2]的值、也就是数值6，其地址换算就是：
100+3*1+2=105
对于一个3维数组，比如：
这样的数组，我们首先按先行后列的次序保存第0页、然后再保存第1页，假设开始地址依然是100，就是：
对于读写数组，比如：a[1][2][1]是在哪里？这个就是数组中的301。
对这个问题，实际就是说找第1页、第2行、第1列的数据是在哪里？
注意这里的编号是按100开始的，在线性内存中怎么找的呢？
首先注意页单位，就是说每页多少个数据，对这个数组，每页12个数据；
其次是每行多少个数据，对这个数组，每行是4个数据；
所以对于a[1][2][1]，就是说：
100+121+24+1=121
从地址121取得的数就是301。
3 映像公式的推导以及多维数组存取地址计算方法
上面的计算过程可以推导出一个公式，如果用LOC(a[i][j])来表示数组a[i][j]的存储地址，用m代表数组的行数、n代表数组的列数，则对二维数组就是：
LOC(a[i][j])=LOC(a[0][0])+n*i+j; (1式)
这个式子默认数组中每个数字仅仅占一字节内存，如果每个数据占用L字节，则有：
LOC(a[i][j])=LOC(a[0][0])+(n*i+j)*L; (2式)
这样的函数就称为数组映像函数，当然这个还很不够，我们再分析三维数组的。从上面的范例可以看出：假如三维数组a[m3][m2][m1]，则对于三维数组就是：
LOC(a[i][j][k])=LOC(a[0][0][0])+im1m2+j*m2+k; (3式)
推广到每个数据L字节，就是：
LOC(a[i][j][k])=LOC(a[0][0][0])+(im1m2+j*m2+k)*L; (4式)
上述过程我们不难推广到N维数组，这个情况下的映像函数见教材P100的(5.2)。这里不再继续推导。
仔细回顾(2式)、(3式)，发现其中有个概念非常关键，就是计算中的n、或者是m1*m2这些计算，它们的物理意义很明确：就是该矩阵每行有几个数？或者是该矩阵每页有几个数？这个计算很有意思，我们假设有数组定义：
a[4][5][6][7][8];
如果要取该数组的a[1][2][3][4][5]中的元素，那么如何计算呢？
首先我们要明白原始的数组定义：a[4][5][6][7][8]是什么意思，这里用书来说明很合适：
8：代表每行8列；
7：代表一页7行；
6：代表每本书6页；
5：代表该书有5册；
4：代表该书有4卷。
说直接点就是：有这么一套书，它由4卷组成、每卷有5册、每册书6页、每页书7行、每行8个数字。这个书中所有的数字都存储在一系列线性排列的方格中，每个方格都有地址，每个方格里存储着一个数字。书在这些方格里是从第0页开始、先行后列逐个存储的。
a[1][2][3][4][5]的含义则是：在上述线性排列的方格里、找其中第1卷、第2册、第3页、第4行、第5列是什么数字？计算出这个数字存储在哪个方格里、取出这个数字，这个过程就是所谓的取数组元素。
这里一定区分数组定义和取其中元素的差别。
重新回头看数组定义：a[4][5][6][7][8]
我们知道：
数组的每行每列总是一个1字符；
每页有7*8=56个字符；
每册有678=332个字符；
每卷有567*8=1680个字符；
该书共有：45678=6720个字符。
再看a[1][2][3][4][5]是寻找第1卷、第2册、第3页、第4行、第5列是什么字？
根据上述每卷每册每页的计算，位置就是：
16720+21680+3332+456+5*1
而6720、1680、332、8、1这些乘积数我们称为数组维单位，它代表着一个下标数相当与几个数字。在编程中，我们命名为constants[]
例1 对数组：int a[2][3][4]，如定义维单位constants，则就是：
constants[ ]={12，4，1};
相当于：每页12个数据、每行4个数据，每列1个数据，对任意数组，每列总是1个数。
读写a[1][2][3]，则位置在：
1* constants[0]+2* constants[1]+3* constants[2]
例2对数组：int b[5][6][7][8][9];
则constants[ ]={6789,789,89,9,1};
如要读b[2][3][4][5][6]，则位置在：
2constants[0]+3 constants[1]+4* constants[2]+5* constants[3]+6* constants[4]
4 程序设计之一：数组的初始化
所以可以设计以下一个表格来表示数组：
struct Array
{
struct ElemType *base; //线性地址的首地址
int dim; //这个数组的维数，如int a[2][3][4]是3维的，dim=3
int *bounds; //每维的大小，就是存储上例中的{2，3，4}
int *constants; //每维的数据个数，{12，4，1}
};
有了上述定义，则初始化函数的模样就是的：
struct Array * Initarray(int dim, ...)
{
函数体
}
这样就可以初始化任意维数的数组，比如：
A1=Initarray(3,2,5,8); //类似 A1[2][5][8]
A2=Initarray(4,2,3,4,5); //类似 A2[2][3][4][5]
A3=Initarray(5,2,3,4,5,6); //类似 A3[2][3][4][5][6]
所以，初始化一个数组，就是按Array的结构、填写一个Array类型的表格，并申请足够大的内存空间来存储这些数据，如下表：
例3 构造A=Initarray(5,2,3,4,5,6)，所以下列表格就是A
<1> 保存各维大小的数据
首先是A->dim=5;
对于每维的大小，要动态申请内存，就是：
A->bounds=(int *)malloc(sizeof(int)*A->dim);
然后让：
A->bounds[0]=2; A->bounds[1]=3; A->bounds[2]=4; A->bounds[3]=5; A->bounds[5]=6;
如同上表所示。
<2>计算维单位
再次申请存储空间、准备计算每维的单位数据个数
A->constants=(int *)malloc(dim*sizeof(int));
计算各个维的单位值：
就是：
A->constants[4]=1；
A->constants[3]= A->bounds[4]* A->constants[4]; 就是6*1
A->constants[2]= A->bounds[3]*A->constants[3]; 就是5*6*1
A->constants[1]= A->bounds[2]*A->constants[2]; 就是4*5*6*1
A->constants[0]= A->bounds[1]*A->constants[1]; 就是3*4*5*6*1
<3>申请数据存储空间
对数组A写成C语言格式，就是：A[2][3][4][5][6]，这个数组总体需要存储空间大小就是：
23456*sizeof(类型)
如果类型是int、并且是在VC下，则就是：
23456sizeof(int)= 234564字节
则申请内存的语句就是：
elemtotal=1;
for(i=0;i<A->dim;i++)
elemtotal= elemtotal*A->dim[i]
A->base=(int *)malloc(elemtotal*sizeof(int));
就是：
我们的编程中，构造的数组并不是简单的int，而是一个很复杂的表ElemType，所以根据这个表，我们整体的数组构造函数如下表：
//必须是可变参数函数，第一个数据是维数
struct Array * Initarray(int dim, ...)
{
struct Array *A;
va_list ap;
int m,i,elemtotal;//elemtotal是数据个数
//读维数，比如InitArray(4,2,4,6,8)，则先读4
va_start(ap,dim);
if (dim<1) return NULL;
//申请一个Array表格的存储空间
A=(struct Array *)malloc(sizeof(struct Array));
A->dim=dim;//写进维数
A->bounds=(int *)malloc(dim*sizeof(int));//申请空间，准备存储2、4、6、8
elemtotal=1;
//读每维的数据个数，如是:
//InitArray(4,2,4,6,8)，则读4次，读2、4、6、8
for (i=0;i<dim;i++)
{
m=va_arg(ap, int);
A->bounds[i]=m;//A->bounds逐次写进2、4、6、8
elemtotal*=m; //乘积，算总共有多少个数据，就是2*4*6*8
}
va_end(ap);
//按总容量申请内存
A->base=(struct ElemType *)malloc(elemtotal*sizeof(struct ElemType));
//申请存储空间、准备计算每维的单位数据个数
A->constants=(int *)malloc(dim*sizeof(int));
//维单位的最后一个总是1，就是每列1个数据：A->constants[3]=1
A->constants[dim-1]=1;
//然后做维数乘积，计算当前维单位，其中A->bounds[]={2,4,6,8};
// A->constants[2]= A->bounds[3]*A->constants[3];=>8*1
// A->constants[1]= A->bounds[2]*A->constants[2];=>6*8*1
// A->constants[0]= A->bounds[1]*A->constants[1];=>4*6*8*1
//就是：
for (i=dim-2;i>=0;i--)
A->constants[i]=A->bounds[i+1]*A->constants[i+1];
//所有Array表项填写完毕
return A;
}
上述过程即初始化一个数组。
5 获得数组中指定下标元素的位置：
这个问题就如同：int a[3][4][5][6]，其中a[1][2][3][4]这个数据在哪里存储着？
因为在初始化这个数组的时候，有维单位数组：
constants[4]={120，30，6，1}
所以数据a[1][2][3][4]应该在：
LOC(a[0][0][0][0])+1* constants[0]+2* constants[1]+3* constants[2]+4* constants[3];
就是：
LOC(a[0][0][0][0])+1120+230+36+41
对LOC(a[0][0][0][0])，程序中就是a->base中。
此处不考虑LOC(a[0][0][0][0])的地址，仅仅计算这个偏移位置，就是：
int Local(struct Array *p,int n, ...)
{
int i,off=0;
va_list ap;
va_start(ap,n);
for (i=0;i<p->dim;i++)
{
off+=p->constants[i] * n;
n=va_arg(ap,int);
}
va_end(ap);
return off;
}
如有：
struct Array *a;
int n;
a=Initarray(4,3,4,5,6);
n=Local(a,1,2,3,4);
这个函数可以获得该数据的位置。同样的道理，也可以获得这个数据存储的地址，有了这个地址，无论读还是写，都是很容易实现的。Ar1.c就是这样的程序范例。
6 数组元素的读写
这个问题就如同：int a[3][4][5][6]，求x=a[1][2][3][4]这个数据在哪里存储着。
读数组数据函数如下，实际和Local()非常相似。
struct ElemType Value(struct Array *p,int n,...)
{
struct ElemType e,*pe;
va_list ap;
int i,off=0;
va_start(ap,n);
for (i=0;i<p->dim;i++)
{
off+=p->constants[i] * n;
n=va_arg(ap,int);
}
va_end(ap);
pe=p->base;
for (i=0;i<off;i++)
pe++;
e=*pe;
return(e);
}
写函数则是：
void Assign(struct Array *p,struct ElemType e,int n,...)
{
va_list ap;
int i,off=0;
struct ElemType *pe;
va_start(ap,n);
for(i=0;i<p->dim;i++)
{
off+=p->constants[i]*n;
n=va_arg(ap,int);
}
va_end(ap);
pe=p->base;
for (i=0;i<off;i++)
pe++;
pe->Data=e.Data;
}
有了这些函数后，整体测试函数见ar1.c，此处不再介绍。这个程序仅仅测试了一个二维数组，实际上可以适合任意维数。
7 稀疏矩阵
稀疏矩阵没什么很明确的定义，基本就是说有大量0的矩阵。这样的矩阵直接存储、将有大量同样的数据存储着、会占用很大的存储空间。所以，压缩这些数据是很有必要的，在随后的介绍中，我们还将介绍一种基于二叉树的数据压缩方法，这里介绍一种简单的、很有针对性的数据压缩方法的实现。
对一个矩阵：
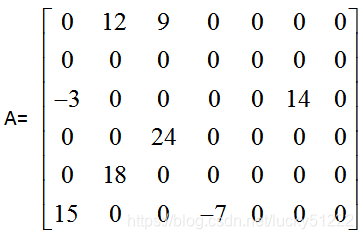可以设计成下面的表格进行计算：
这样的表格存储稀疏矩阵，将能大大减少存储量，如果矩阵的数据是双精度的，则节省的存储空间要更多一些。
表1的设计、如果用C语言表述，就是：
struct ElemType
{
int D;
};
struct Triple
{
int i,j;
struct ElemType e;
};
注意这里没设计成：
struct Triple
{
int i,j;
int D;
};
我们把数据专门设计成一个ElemType类型的表，则表明矩阵实际可以是任何类型，仅仅修改这个表中的数据类型，将基本满足大多情况下的需求。而后者则受限制很多。上面的设计中，Triple说明了表1中的一行，整个表格就是：
struct TSMatrix
{
struct Triple *data;
int nu,mu,tu;
};
struct Triple *data;是表格数据的首地址；
int nu,mu,tu;分别是数据的行、列、以及总数据个数。现在我们就编写一个压缩稀疏矩阵的程序。首先，我们要编写一个初始化函数CreatSMatrix()，实际就是填写下面的表格：
<1>
如上例的矩阵A，有6行7列，于是有：
<2>
统计非0元素的个数，这个程序很简单，就是：
int I,j,sz=0;
for (i=0;i<n;i++)
for (j=0;j<m;j++)
if (A[i][j]!=0) sz++;
于是表格里就是：
<3>
根据非0个数申请内存，就是：
(struct Triple *)malloc(sizeof(struct ElemType)*sz);
可以看出这是个顺序表的构造方法，实际中，一个矩阵的大小一旦确定，确实是不会删除一行、或者是中间随意插入一行的，这样，顺序表的做法是很合适的。
<4>
被调函数中如何访问主调函数中的二维数组？这是个非常关键的问题，在此，我们首先假设编写这个被调函数时、并不知道一个矩阵有多大，而只有主调函数中才能知道大小。于是我们把这个函数的参数确定为：
CreatSMatrix(int **pA,int n,int m)
其中**pA代表指向二维数组的行首地址，n、m分别是矩阵的行列数。
比如在main()中，一个数组如下：
int A[6][7]={
{0,12,9,0,0,0,0},{0,0,0,0,0,0,0},{-3,0,0,0,0,14,0},
{0,0,24,0,0,0,0},{0,18,0,0,0,0,0},{15,0,0,-7,0,0,0}
};
这是一个6行7列的数组，其中A[0]、A[1]、A[2]、A[3]、A[4]、A[5]分别代表每行的首地址，这个概念很重要，于是：
int *Da[6];
for(i=0;i<6;i++) Da[i]=A[i];
则就是用指针数组Da[]保存了每行的首地址，于是这个情况下，调用函数就是：
CreatSMatrix(Da,6,7);
注意：在用函数虚实结合方式访问一个二维数组，必须知道每行的首地址，否则不能正确读取数据。
通过这样的手段，一个二维数组就通过虚实结合的方式、能被函数访问了。
struct TSMatrix * CreatSMatrix(int **pA,int n,int m)
{
int i,j,sz=0;
struct TSMatrix *p;
struct Triple *pe;
p=(struct TSMatrix *)malloc(sizeof(struct TSMatrix));
//计算非0元素的个数
for (i=0;i<n;i++)
for (j=0;j<m;j++)
if (pA[i][j]!=0)
sz++;
p->nu=n;p->mu=m;p->tu=sz;
p->data=(struct Triple *)malloc(sizeof(struct ElemType)*sz);
//将非0的元素写进数据表
pe=p->data;
for (i=0;i<n;i++)
for(j=0;j<m;j++)
if (pA[i][j]!=0)
{
pe->i=i;pe->j=j;
pe->e.D=pA[i][j];
pe++;
}
return p;
}
读写函数是简单的，请同学们自己补充读写函数。程序ar2.c是这个函数的测试程序。
附： 线性方程组的求解程序分析
线性方程的求解过程，典型的方法是高斯消元法法。我们这里要用计算机求解，首先是要针对任意规模的线性方程，而不仅仅是常规的3、4元方程。当然，算法分析阶段还是简单的方程为例。
这个式子写成矩阵表达式，就是：
计算这个式子，是一个典型的表格加工过程，首先是有表格：
<1>
这个表格如果写成矩阵，在线性代数里称为增广矩阵。
<2>
逐行消元就是先把第2行第1列通过加减消元，也就是第1行所有列乘5，加第2行各列，于是有：
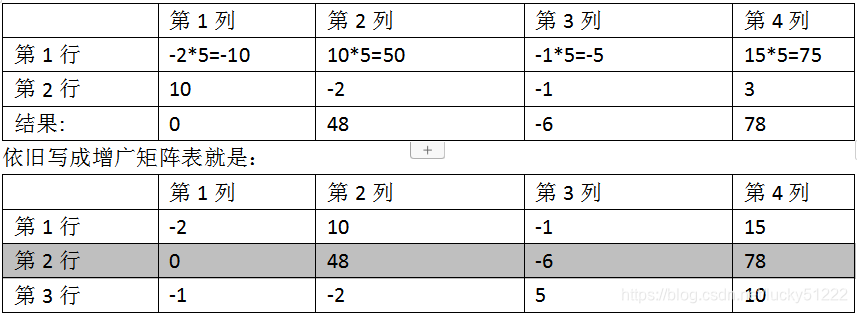用样的手段处理第3行，就是第1行乘1/2后、减第3行，结果就是：
<3>
根据上面的结果，再次消元，目的是将第3行第2列-7变成0，于是就是将第3行各列都乘48/7，与第2行加，结果就是：
这样，就是把原式逐步消减为下面的式子：
这个式子计算X3非常容易，然后逐个求解其他未知变量即可。
Ar3.c是一个多元方程组的计算程序，它会从d.txt中读到原始的方程组系数数据，修改这个文件中的数据，就能计算相应的多元一次方程。关于这个程序的全部运行过程不再介绍。
8 作业：
1 设计一个压缩多维稀疏矩阵的程序；
2 程序见ar3.c，自己设计表格、画出这个程序解上述方程组的整个运行过程。