c/c++ 编程试题
带*号为选作题,给出代码截屏和编译运算结果截屏
1.编程:选取M个最大的数 编程实现从N个无序数中选取M个最大的数(0 < M < N )
思路:通过冒泡排序或者选择排序对N个数进行递减排序,然后输入前M个数即可。这里我想到的是通过数组来存储这N个数。
#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
int i,j,t,N,M,a[1000];
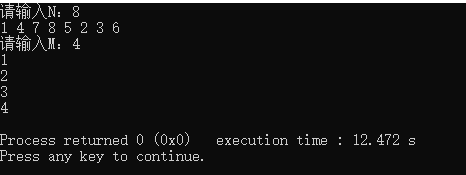
printf("请输入N:");
scanf("%d",&N);
for(i=0;i<N;i++)
{
scanf("%d",&a[i]);
}
for(i=0;i<N-1;i++)
{
for(j=0;j<N-1-i;j++)
{
if(a[j]>a[j+1])
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
}
}
printf("请输入M:");
scanf("%d",&M);
for(j=0;j<M;j++)
{
printf("%d\n",a[j]);
}
return 0;
}
2.编程:断开链条 给定一个包含N个整数的数组A,假设这个数组表示的是一条链条,其中 每个元素表示链条上的一环。现在我们想把这条链条断成3小部分。我们需 要做的就是断开不相连的两个环,比如,我们需要断开环P、Q
(0<P<Q<N-1, Q-P > 1),得到三个小链条[0,P-1],[P+1,Q-1],[Q+1,N-1]。
上述操作的成本是A[P]+A[Q]。 例如:数组A为 A[0] = 5 A[1] = 2 A[2] = 4 A[3] = 6 A[4] =
3 A[5] = 7 我们可以选择如下方式断开链条
- (1,3):成本是 2+6 = 8
- (1,4):成本是 2+3 = 5
- (2,4):成本是 4+3 = 7 写一个函数如int breakchain(参数列表自定义); 对任一个给定的链条,返回断开链条的最低成本,比如上面的例子中, 需要返回最低成本5 假设:
- N是整数,范围[5,100000] A的元素是范围在[1,1000000000]的整数
3.编程:顺时针环绕列印矩阵元素 给定一个整数元素组成的矩阵,写一个函数,返回一个数组,数组中的元 素是按照顺时针遍历矩阵中的元素而组成。例如如下的3x4矩阵: 2, 3, 4, 8 5, 7, 9, 12 1, 0, 6, 10
得到的数组的元素按照顺序是“2, 3, 4, 8, 12, 10, 6, 0, 1, 5, 7, 9”.
我读完该题的时候脑子里面想到了《算法竞赛 入门经典 第2版》里面P40页的蛇形填数问题。
即:在n * n方阵里填入1,2,…,n*n,要求填成蛇形。例如,n=4时方阵为:
10 11 12 1
9 16 13 2
8 15 14 3
7 6 5 4
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
#define maxn 20
int a[maxn][maxn];
using namespace std;
int main()
{
int n,x,y,tot = 0;
scanf("%d",&n);
memset(a,0,sizeof(a));
tot = a[x=0][y=n-1] = 1;
while(tot < n*n){
while(x+1 < n && !a[x+1][y]) a[++x][y]=++tot;
while(y-1 >=0 && !a[x][y-1]) a[x][--y]=++tot;
while(x-1 >=0 && !a[x-1][y]) a[--x][y]=++tot;
while(y+1 < n && !a[x][y+1]) a[x][++y]=++tot;
}
for(x = 0;x < n;x++){
for(y=0;y<n;y++)printf("%3d",a[x][y]);
printf("\n");
}
return 0;
}
当然这道题可以参考蛇形填数来进行改编
4.编程:最大方形长度 给定一个元素是布尔型大小为NM的矩阵A。大小为L的方形可以放置在A 中的(X,Y)处,如果满足: 0 < L <= min(N,M) - 1 0 <= X <= N-L 0 <= Y <= M-L A[X+i][Y+j] = true, 0 <= i
< L, 0 <= j < L 如果L能被放置在(X,Y)以及(X+1,Y)或者(X,Y+1),我们说它可以被
从(X,Y)移动到(X+1,Y)或者(X,Y+1)。 我们想找出满足以下条件的最大的L: L可以被放置在(0,0)(假如此处为true)
它可以被经过一系列的移动,从(0,0)到达(N-L,M-L)
换言之,我们想找到最大的方形,可以从为true的左上移动到为true的右下,该方形覆盖的区域都是true,移动方式是向下或者向右移动。一个极端情况是如果矩阵A中的元素全部是true,那
么L = min(N,M) - 1。 写一个函数:比如int moveSquare(参数列表自定义); 返回值为L。 比如:
A[0][0]=true A[0][1]=true A[0][2]=true A[0][3]=false A[1][0]=true
A[1][1]=true A[1][2]=true A[1][3]=false A[2][0]=true A[2][1]=true
A[2][2]=true A[2][3]=false A[3][0]=true A[3][1]=true A[3][2]=true
A[3][3]=true A[4][0]=false A[4][1]=true A[4][2]=true A[4][3]=true
A[5][0]=true A[5][1]=false A[5][2]=true A[5][3]=true 返回 2
A[0][0]=true A[0][1]=true A[0][2]=false A[0][3]=false A[1][0]=true
A[1][1]=false A[1][2]=false A[1][3]=false A[2][0]=false
A[2][1]=true A[2][2]=false A[2][3]=true 返回 0 A[1][1]=true 返回 1
假设N和M是范围为[1,200]的整数
5.*问答题(建议编程实现)
假设你站在120层摩天大楼的天台,手握两个iphone
x,并且可轻易到达任一楼层的阳台。请用最少的尝试次数nTry,确定能够让iphone自由下落而不会摔坏的最高层数nMaxLayer。比如20层摔不坏,21层摔坏,则nMaxLayer=21。在尝试中你可以摔坏这两个iphone,只要能得到答案。请说明最坏情况需要多少次尝试以及你的思路。