[C++知识库]C++ 实现选择排序 算法详解

算法原理

原理简述

1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
2. 再从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾
3. 以此类推，直到所有元素均排序完毕

过程分析

如下图所示：

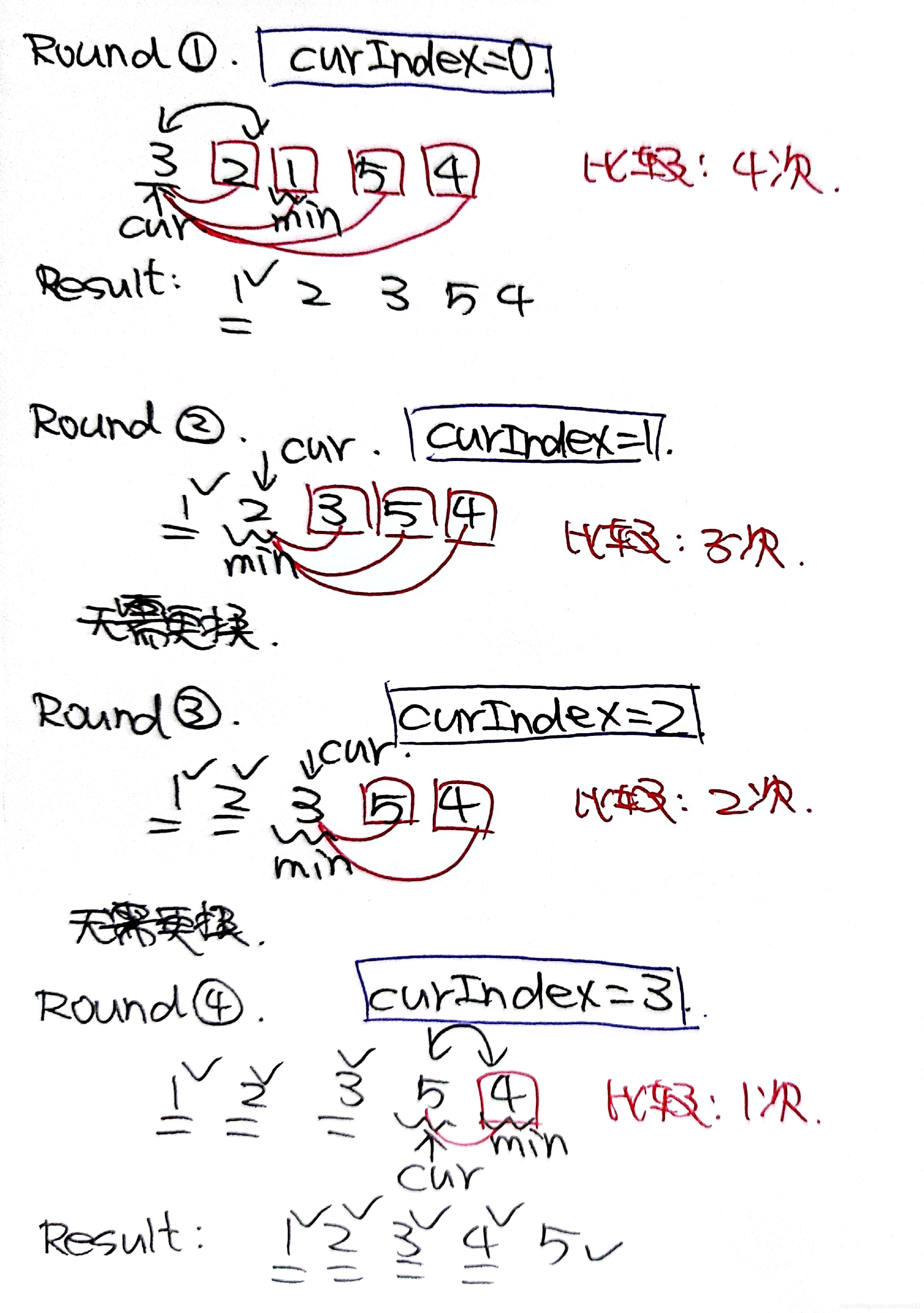
分析总结

可以用两层循环来实现此算法：

第一层循环是?(curIndex = 0; curIndex < len - 1; curIndex++)

第二层循环是?(i = curIndex + 1; i < len; i++)

代码实现

// 交换两数
void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 选择排序
void selectionSort(int arr[], int len) {
    int curIndex = 0;
    int minIndex = 0;
    int i = 0;

    for (curIndex = 0; curIndex < len - 1; curIndex++) {
        minIndex = curIndex;
        for (i = curIndex + 1; i < len; i++) {
            if (arr[minIndex] > arr[i]) {
                minIndex = i;
            }
        }
        swap(&arr[curIndex], &arr[minIndex]); // 交换
    }

}

时间复杂度

与冒泡排序相似，假设需要排序的数组长度为n，则：

该算法中循环语句执行总次数：.

时间复杂度取 T(n) 最高次项，即?.