题目描述
对于一个 n 个顶点的凸多边形,它的任何三条对角线都不会交于一点。请求出图形中对角线交点的个数。
例如,6 边形:
输入格式
输入只有一行一个整数 n,代表边数。
输出格式
输出一行一个整数代表答案。
输入样例 1
3
输出样例 1
0
输入样例 2
6
输出样例 2
15
说明/提示
数据规模与约定
对于 50% 的数据,保证 3 ≤ \leq ≤ n ≤ \leq ≤ 100。 对于100%的数据,保证 3 ≤ \leq ≤ n ≤ \leq ≤ 105。
题目分析
QAQ,因为之前并没有接触过对角线的相关问题,然后我也没想到能推公式。所以这个题目我是自己画图推的。
我的想法是:
因为题目说“它的任何三条对角线都不会交于一点”,所以我们只需要考虑有多少个两两之间的对角线会相交就可以了。
然后如何计算一个对角线会和几个对角线相交呢,我想到的是如果先定下两个顶点之间的对角线A,另一条对角线B要和它相交,那么另一条对角线B的两个顶点一定是分别在这个定下的对角线A的两侧。
所以这个对角线上有几个交点就等于,这个对角线的右边顶点数 * 左边顶点数。
假设为 8 边形,因为该对角线自己要占用两个顶点,所以其左右顶点之和为8 - 2 = 6。
那么该对角线上的交点就一共有以下几种情况:
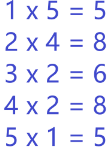
而多边形的每一个顶点上,刚好可以取得和上述五种情况对应的对角线。
所以可得每个顶点的所有对角线上的交点为
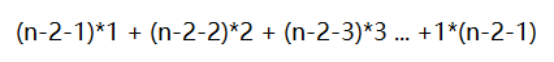
如果将一个顶点的总交点数乘以顶点数,得到的值是将每个顶点都算了四次的值,所以再除以4就可以得到总的交点数。
算了四次的原因是,一个交点是由两个对角线参与的,然后我们算了每个顶点的每个对角线,所以每个对角线我们都算了两次,而又将两个对角线的先后顺序交换算了一次交点,所以一共计算了2*2次
参考代码
因为3 ≤ \leq ≤ n ≤ \leq ≤ 105,所以计算结果比较大,我最开始只是用long long,但是结果还是会有两个WA,后来我发现了高精———unsigned long long,就可以AC啦。
#include "stdio.h"
//交点数等于每个顶点出发的对角线的交点数相加 / 4
//每个对角线上的交点数等于 该对角线左边的顶点乘以右边的顶点
//所以每个顶点的交点数为 (n-2-1)*1 + (n-2-2)*2 + (n-2-3)*3 ... +1*(n-2-1)
/*
*计算每个顶点出发的对角线的交点
*@Param sideCount:int 多边形的边数量
*/
unsigned long long intersectionEachVertex(unsigned long long sideCount){
//交点数量
unsigned long long intersection = 0;
for(int i = 1;i <= sideCount - 2 - 1; i++){
intersection += (sideCount - 2 - i) * i;
}
return intersection;
}
int main(){
//多边形的边数
unsigned long long sideCount;
//输入多边形的边数
scanf("%lld",&sideCount);
//计算每个顶点出发的对角线的交点
unsigned long long intersection = intersectionEachVertex(sideCount);
printf("%lld",intersection * (unsigned long long)sideCount / 4);
return 0;
}
如果有帮助到您,请帮我点个赞哦。
如果对本文章有疑问,欢迎在评论区留言。
😁