Prim算法
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。
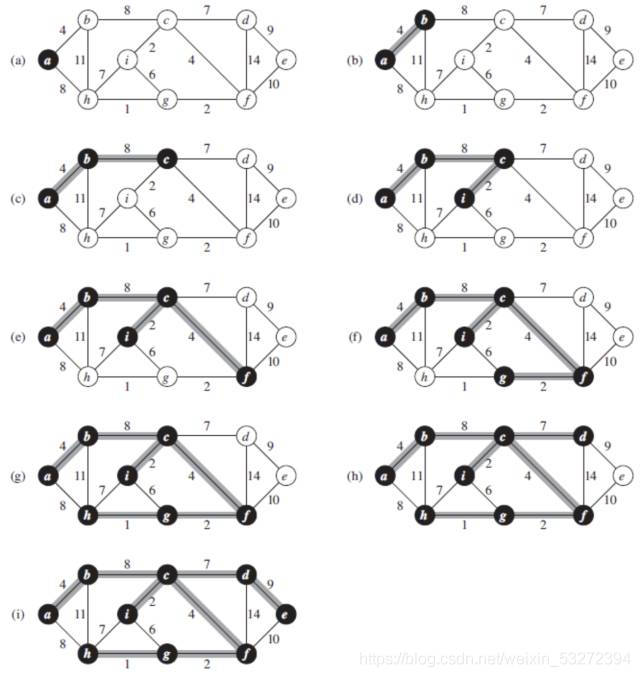
假设V是图中顶点的集合,E是图中边的集合,TE为最小生成树中的边的集合,则prim算法通过以下步骤可以得到最小生成树:
1:初始化:U={u 0},TE={f}。此步骤设立一个只有结点u 0的结点集U和一个空的边集TE作为最小生成树的初始形态,在随后的算法执行中,这个形态会不断的发生变化,直到得到最小生成树为止。
2:在所有u∈U,v∈V-U的边(u,v)∈E中,找一条权最小的边(u 0,v 0),将此边加进集合TE中,并将此边的非U中顶点加入U中。此步骤的功能是在边集E中找一条边,要求这条边满足以下条件:首先边的两个顶点要分别在顶点集合U和V-U中,其次边的权要最小。找到这条边以后,把这条边放到边集TE中,并把这条边上不在U中的那个顶点加入到U中。这一步骤在算法中应执行多次,每执行一次,集合TE和U都将发生变化,分别增加一条边和一个顶点,因此,TE和U是两个动态的集合,这一点在理解算法时要密切注意。
3:如果U=V,则算法结束;否则重复步骤2。可以把本步骤看成循环终止条件。我们可以算出当U=V时,步骤2共执行了n-1次(设n为图中顶点的数目),TE中也增加了n-1条边,这n-1条边就是需要求出的最小生成树的边。
n个顶点 n-1 条边 n-1条边的路径之和最短
n-1条边要把所有的顶点连接在一起
n-1条边的权重相加最小,则称为最小生成树
prim 普里姆 普拉姆 稠密图
每次从未加入到生成树的集合中选择一条到生成树中
(任意一个顶点都行)最短路径的边所接连的顶点
加入到生成树中
重复n-1次
//普里姆最小生树算法
#define MAX_INT (~(1<<31))
void prim(ALGraph *pg){//O(|V|*|V|+|E|))
int dist[pg->vexnum]; //保存未加入到生成树的所有顶点到达生成树中的距离
int begv[pg->vexnum]; //begv[i]记录到顶点i的最短距离的边的开始顶点
//dist[i] 表示 到顶点i的距离 dist[i]==0 表示i顶点已经在生成树中了
int i,j;
for(i=0;i<pg->vexnum;i++){
dist[i] = MAX_INT; //最大值 表示一开始到生成树的距离无穷大
begv[i] = -1;
}
int curr = 0;
for(i=0;i<pg->vexnum-1;i++){//循环pg->vexnum-1次
dist[curr] = 0;//curr顶点加入到生成树中
ArcNode *node = pg->vexs[curr].firstarc;
//更新未加入到生成树中的所有顶点到生成树中顶点的距离
for(;node!=NULL;node=node->next){
//node->adjvex不在生成树中 它到生成树的距离比之前小
if(dist[node->adjvex]!=0 && node->weight < dist[node->adjvex]){
dist[node->adjvex] = node->weight;
begv[node->adjvex] = curr;//该距离是从curr到node->adjvex顶点
}
}
int min = 0;
for(j=1;j<pg->vexnum;j++){//选取一条到生成树中最小的边
if((dist[j]!=0&&dist[j]<dist[min])||dist[min]==0){
min = j;
}
}
printf("%c -[%d]-> %c\n",pg->vexs[begv[min]].data,dist[min],pg->vexs[min].data);
curr = min;
}
}
Kruskal算法
求加权连通图的最小生成树的算法。kruskal算法总共选择n- 1条边,(共n个点)所使用的贪心准则是:从剩下的边中选择一条不会产生环路的具有最小耗费的边加入已选择的边的集合中。注意到所选取的边若产生环路则不可能形成一棵生成树。kruskal算法分e 步,其中e 是网络中边的数目。按耗费递增的顺序来考虑这e 条边,每次考虑一条边。当考虑某条边时,若将其加入到已选边的集合中会出现环路,则将其抛弃,否则,将它选入。
假设V是图中顶点的集合,E是图中边的集合,TE为最小生成树中的边的集合,则prim算法通过以下步骤可以得到最小生成树:
1:初始化:U={u 0},TE={f}。此步骤设立一个只有结点u 0的结点集U和一个空的边集TE作为最小生成树的初始形态,在随后的算法执行中,这个形态会不断的发生变化,直到得到最小生成树为止。
2:在所有u∈U,v∈V-U的边(u,v)∈E中,找一条权最小的边(u 0,v 0),将此边加进集合TE中,并将此边的非U中顶点加入U中。此步骤的功能是在边集E中找一条边,要求这条边满足以下条件:首先边的两个顶点要分别在顶点集合U和V-U中,其次边的权要最小。找到这条边以后,把这条边放到边集TE中,并把这条边上不在U中的那个顶点加入到U中。这一步骤在算法中应执行多次,每执行一次,集合TE和U都将发生变化,分别增加一条边和一个顶点,因此,TE和U是两个动态的集合,这一点在理解算法时要密切注意。
3:如果U=V,则算法结束;否则重复步骤2。可以把本步骤看成循环终止条件。我们可以算出当U=V时,步骤2共执行了n-1次(设n为图中顶点的数目),TE中也增加了n-1条边,这n-1条边就是需要求出的最小生成树的边。
 kruskal 克鲁斯卡尔 稀疏图
kruskal 克鲁斯卡尔 稀疏图
对所有的边进行排序 (从小到大)
从边权重最小的开始选择,试着加入到生成树,
***如果和之前的顶点能够成回路则舍弃
如果没有构成回路则该条边是合适的
总共选择n-1条边
int comp_path(const void *v1,const void *v2){
const Path *pa = (const Path*)v1;
const Path *pb = (const Path*)v2;
return pa->weight - pb->weight;
}
//与curr顶点相连的最开始的顶点
static int find_src(int flag[],int curr){
while(flag[curr]!=curr){
curr = flag[curr];
}
return curr;
}
void kruskal(ALGraph *pg){//O(|V|+|E|log|E|)
Path path[pg->arcnum];
int j = 0;
int i;
for(i=0;i<pg->vexnum;i++){//O(|E|+|V|)
ArcNode *node = pg->vexs[i].firstarc;
for(;node!=NULL;node = node->next){
//i node->adjvex node->weight
if(i>node->adjvex && (pg->kind==UDG||pg->kind==UDN)){
continue;
}
path[j].ibeg = i;
path[j].iend = node->adjvex;
path[j].weight = node->weight;
++j;
}
}
qsort(path,pg->arcnum,sizeof(Path),comp_path);//O(|E|log|E|)
int cnt = 0;//记录选取的边数
int flag[pg->vexnum];
for(i=0;i<pg->vexnum;i++)
flag[i] = i;
for(i=0;i<pg->arcnum&&cnt<pg->vexnum-1;i++){//O(|V|)
int src1 = find_src(flag,path[i].ibeg);
int src2 = find_src(flag,path[i].iend);
if(src1!=src2){//说明ibeg,iend 连接的边 选取之后 不会构成回路
printf("%c -[%d]-> %c\n",pg->vexs[path[i].ibeg].data,path[i].weight,
pg->vexs[path[i].iend].data);
cnt++;
flag[src1] = src2;
}
}
}