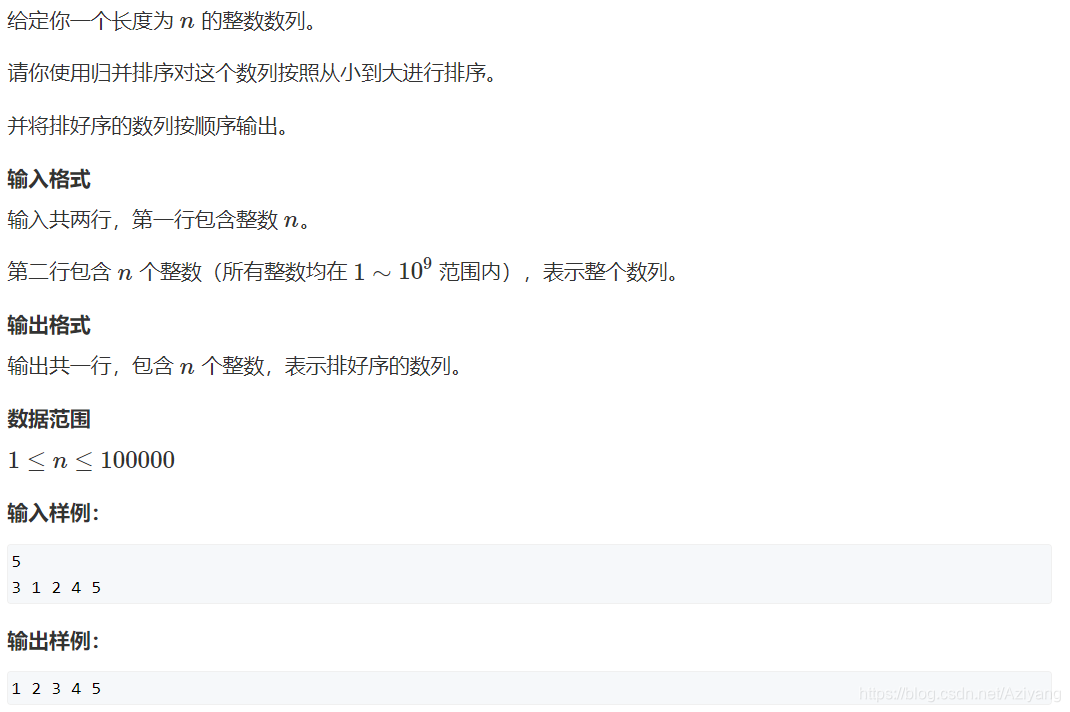
归并排序简单介绍

归并排序

归并排序简单介绍
前言
一、归并排序是什么？
- 这里我们用一个题目来讲解
二、使用步骤
三.强化训练
- 1.例题介绍
总结

前言

我们会经常处理排序的问题，归并排序就是排序当中的一种

提示：以下是本篇文章正文内容，下面案例可供参考

一、归并排序是什么？

归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列;即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序是一种稳定的排序方法。

这里我们用一个题目来讲解

AcWing 787. 归并排序
在这里插入图片描述

二、使用步骤

1.处理分界点

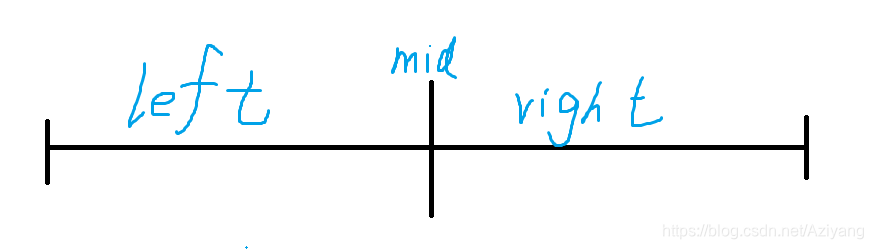
在这里插入图片描述

此时分界点 mid = l + r >> 1 l + r >> 1 就是 (l + r) / 2
代码如下（示例）：

int mid = l + r >> 1;

2.递归排序left和right

处理好分解点之后我们就把分好的左右两边的值都进行递归
此时需要运用的merge_sort 函数
代码如下（示例）：

merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);

3. 归并————合二为一

此时我们需要把处理好的的left和right合并在一起
在这里插入图片描述
总结上述3点我们处理的代码如下

#include<iostream>

using namespace std;

const int N = 1e5 + 10;

int q[N], ans[N]; // ans用来存储我们得到的正确排序
int n;

void merge_sort(int q[], int l, int r)  // 归并排序
{
    if(l >= r) return ;
    int mid = l + r >> 1;
    
    merge_sort(q, l, mid); //将left递归
    merge_sort(q, mid + 1, r); //将right递归
    
    int k = 1, i = l, j = mid + 1; //k = 1，将ans设成下表为k = 1开始的数组
    while(i <= mid && j <= r)
    {
        if(q[i] <= q[j]) ans[k ++] = q[i ++];
        else ans[k ++] = q[j ++]; // 将两个数组合并在一起
    }
    while(i <= mid) ans[k ++] = q[i ++]; //存储剩下还未放入的数组
    while(j <= r) ans[k ++] = q[j ++];
    
    for (i = l, j = 1; i <= r; i++, j++) q[i] = ans[j];
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n ; i++) cin >> q[i];
    
    merge_sort(q, 1, n);
    
    for (int i = 1; i <= n; i ++ ) cout << q[i] << " "; 
    
    cout << endl;
    
    return 0;
}

三.强化训练

1.例题介绍

Acwing788. 逆序对的数量
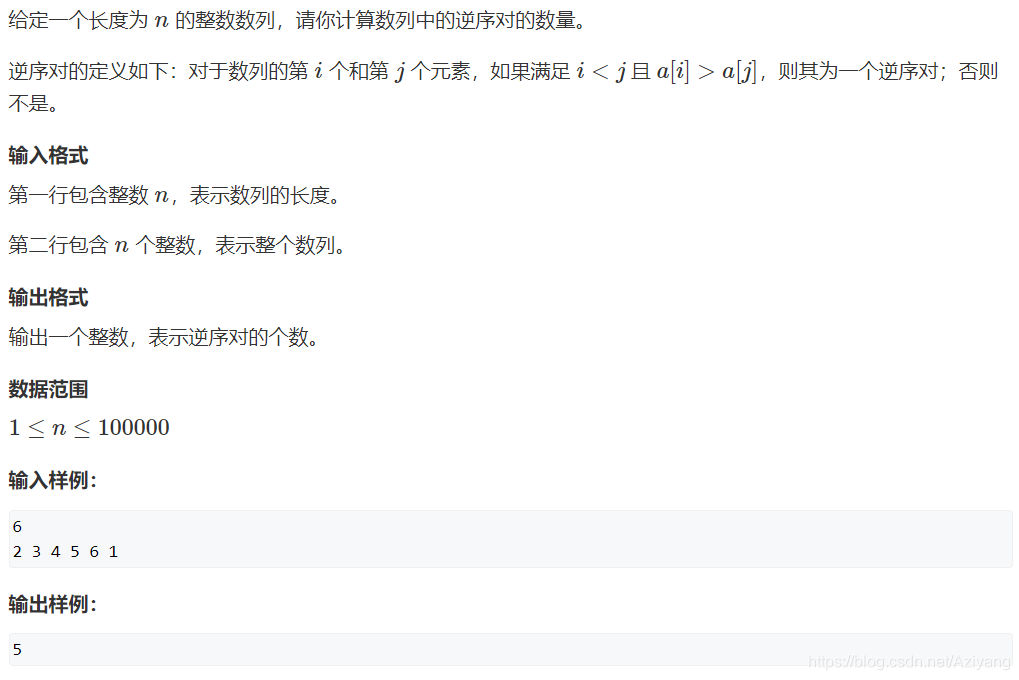
在这里插入图片描述
这个题呢其实只需要在判断q[i] > q[j]的时候加上一个res += mid - i + 1;
见代码如下

#include<iostream>

using namespace std;

typedef long long LL; //因为该题的数据会有点大
const int N = 1e5 + 10;

int q[N], ans[N];
int n;

LL merge_sort(int l, int r)  // 归并排序
{
    if(l >= r) return 0;
    int mid = l + r >> 1;
    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);
    //加上left和right递归排序的时候的q[i] > q[j]时的次数
    
    //归并的过程
    int k = 1, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(q[i] <= q[j]) ans[k ++] = q[i ++];
        else 
        {
            ans[k ++] = q[j ++];
            res += mid - i + 1;
        }
    }
    while(i <= mid) ans[k ++] = q[i ++]; 
    while(j <= r) ans[k ++] = q[j ++];
    
    for (i = l, j = 1; i <= r; i++, j++) q[i] = ans[j];
    
    return res;
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n ; i++) cin >> q[i];
    

    
    cout << merge_sort(1, n) << endl;
    //for (int i = 1; i <= n; i ++ ) cout << q[i] << " "; 
    
    
    return 0;
}