阵图思路
- 准备两个二维数组
- 一个用来存放雷的位置, 下面我称之为雷阵图
- 一个记录玩家扫雷的坐标(扫雷图)
定义的变量:
#define ROW 9
#define COL 9
#define ROWS ROW + 2
#define COLS COL + 2
重点: 使用递归函数实现扫雷中
散花效果
雷阵图
假如我要创建一个9*9的 坐标图盘, 那么就要创建一个11*11的二维数组, 原因就是要实现任一点周围都要有8个坐标, 这样方便我们计算这个点周围的有多少个雷.
char mine[11][11] = { 0 };
然后把这个数组进行初始化, 就是把这个数组里的每一个值都赋值为字符0,
InitBoard(mine, 11, 11, '0');
//初始化数组-----初始化雷盘:这个数组为雷的存放位置
void InitBoard(char board[11][11], int row, int col, char set)
{
int i = 0;
int j = 0;
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
board[i][j] = set;
}
}
}
这个时候数组内每一个值都为字符0, 然后把数组按照每一行进行打印得到

这时进行随机布置雷, 把雷放置在如下图

代码实现:
//布置雷
SetMine(mine, ROW, COL);
//布置雷
void SetMine(char board[ROWS][COLS], int row, int col)
{
int x = 0;
int y = 0;
int count = EASY_COUNT;
while (count)
{
x = rand() % ROW + 1; //模9余 (0 1 2 3 4 5 6 7 8) 然后加上 1
y = rand() % COL + 1;
if (board[x][y] == '0')
{
board[x][y] = '1';
count--;
}
}
}
扫雷图
思路与雷阵图一样, 也是要创建一个9*9的 坐标图盘, 那么就要创建一个11*11的二维数组, 唯一不同的地方在于, 初始化这个数组的时候是吧字符数组初始化为如下

实现代码
//扫雷图二维数组(玩家探索图)
char show[ROWS][COLS] = { 0 };
//初始化扫雷图二维数组
InitDisplayBoard(show, ROWS, COLS, '*');
//这个是扫雷图: 玩家看到的阵图.记录玩家的查询痕迹
void InitDisplayBoard(char board[ROWS][COLS], int row, int col, char set)
{
int i = 0;
int j = 0;
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
board[i][j] = set;
if ((i == 0) || (i == (row - 1)) || (j == (col-1)) || (j == 0))
{ // 此处判断的是第一行与最后一行还有其它行的首位
board[i][j] = ' ';
}
}
}
}
核心代码-递归函数实现(散花效果)
- 确定一个
不是雷的坐标后,(是雷就直接让结束游戏啦) - 先判断这个坐标在扫雷图上面为字符
*,代表这个坐标是在内部9*9格子中并且是第一次进行判断,则继续向下走,否则直接return 0(避免栈溢出,以及不判断扫雷图外围一圈的坐标) - 再判断它周围8个坐标中有多少个为雷. 如果没有雷, 则把这个坐标赋值为
空格, 并进行递归, 如果有雷则把该坐标赋值为字符x(x代表雷的数量)
代码:
//查找这个坐标周围的雷的个数
int find_mine_count(char mine[ROWS][COLS], char show[ROWS][COLS], int x, int y)
{
return mine[x - 1][y - 1] +
mine[x - 1][y] +
mine[x - 1][y + 1] +
mine[x][y - 1] +
mine[x][y + 1] +
mine[x + 1][y - 1] +
mine[x + 1][y] +
mine[x + 1][y + 1] - 8 *'0';
}
#define 说明: 字符1减去字符0得到的结果就是数字 1
//散花效果---递归函数
int find_show_count(char mine[ROWS][COLS], char show[ROWS][COLS], int x, int y)
{
int m_count = 0;
m_count = find_mine_count(mine, show, x, y);
if (show[x][y] == '*')
{
if (m_count == 0)
{
show[x][y] = ' ';
return 1 + find_show_count(mine, show, x - 1, y - 1) +
find_show_count(mine, show, x - 1, y) +
find_show_count(mine, show, x - 1, y + 1) +
find_show_count(mine, show, x, y - 1) +
find_show_count(mine, show, x, y + 1) +
find_show_count(mine, show, x + 1, y - 1) +
find_show_count(mine, show, x + 1, y) +
find_show_count(mine, show, x + 1, y + 1);
}
else
{
show[x][y] = '0' + m_count;
return 1;
}
}
else
{
return 0;
}
}
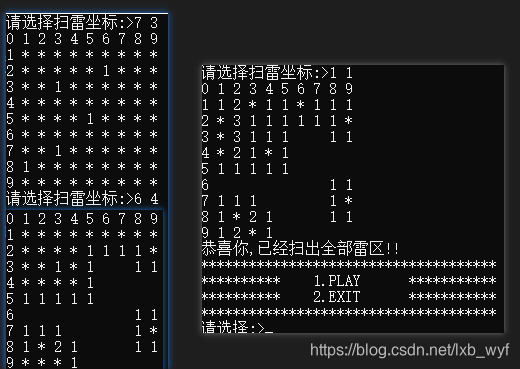
完整代码
GITEE: 完整代码