前面的话:
学习了这么多C语言知识,你会熟练地应用它吗?今天博主将介绍使用C语言实现著名的杨辉三角,来探究这其中的奥秘!
作者水平很有限,如果发现错误,一定要及时告知作者哦!感谢感谢!
博主的码云gitee,平常博主写的程序代码都在里面。
杨辉三角概述
杨辉三角形,又称贾宪三角形,帕斯卡三角形,是二项式系数在三角形中的一种几何排列。在我国南宋数学家杨辉所著的《详解九章算术》(1261年)一书中用如图的三角形解释二项和的乘方规律。
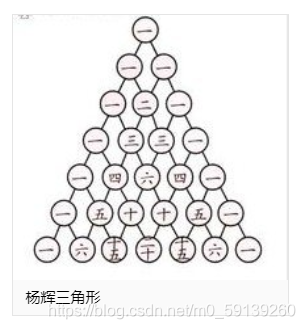
C语言实现杨辉三角
杨辉三角例题:
杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的优美结合。尝试使用编程,打印杨辉三角前10行。
要使用编程打印杨辉三角,必须知道杨辉三角的一些基本性质:
💡杨辉三角每行第一个数和最后一个数为1。
💡杨辉三角第n行数字的个数为n。
💡设一个杨辉三角有n行m列(0<n<21,0<m<21),并将这个杨辉三角所有元素对应行列存入二维数组tri[20][20]中,n>2时,则tri[n][m] = tri[n-1][m-1] +tri[n-1][m]。
所以我们可以以tri[n][m] = tri[n-1][m-1] +tri[n-1][m]为突破口,解决这道题。
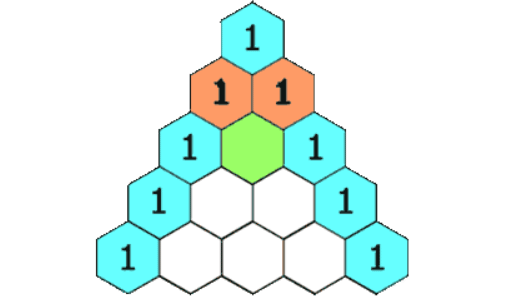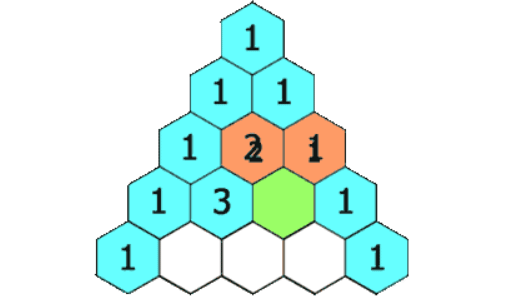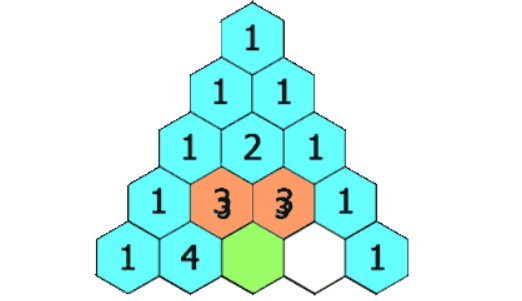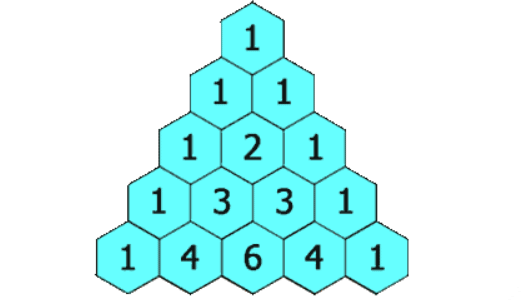
非等腰打印:
#define _CRT_SECURE_NO_WARNINGS 1
#define N 22
#include <stdio.h>
int main()
{
int n = 0;//行数
int arr[N][N] = { 0 };//存放杨辉三角的数据
int i = 0;
int j = 0;
//printf("请输入所需杨辉三角的行数(max=10):");
//scanf("%d", &n);
n = 10;
//creat triangle
for (i = 0; i < n; i++)
{
arr[i][0] = 1;
arr[i][i] = 1;
for (j = 1; j < i ; j++)
{
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
}
//output triangle 非等腰
for (i = 0; i < n; i++)
{
for (j = 0; j < i + 1; j++)
{
printf("%4d", arr[i][j]);
}
printf("\n");
}
return 0;
}
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
D:\gtee\C-learning-code-and-project\YangHuiTriangle\Debug\YangHuiTriangle.exe (进程 30012)已退出,代码为 0。
按任意键关闭此窗口. . .
等腰打印:
#define _CRT_SECURE_NO_WARNINGS 1
#define N 22
#include <stdio.h>
int main()
{
int n = 0;//行数
int arr[N][N] = { 0 };//存放杨辉三角的数据
int i = 0;
int j = 0;
//printf("请输入所需杨辉三角的行数(max=10):");
//scanf("%d", &n);
n = 10;
//creat triangle
for (i = 0; i < n; i++)
{
arr[i][0] = 1;
arr[i][i] = 1;
for (j = 1; j < i ; j++)
{
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
}
//output triangle 等腰
for (i = 0; i < n; i++)
{
for (j = 0; j < n - i - 1 ; j++)
{
printf(" ");
}
for (j = 0; j < i + 1; j++)
{
printf("%4d",arr[i][j]);
}
printf("\n");
}
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
D:\gtee\C-learning-code-and-project\YangHuiTriangle\Debug\YangHuiTriangle.exe (进程 30012)已退出,代码为 0。
按任意键关闭此窗口. . .