一、归并排序MergeSort
归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略,分治法将问题分成一些小的问题然后递归求解,而治的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之。归并排序的时间复杂度为nlog2n。
二、图解
下面用一张图了解用分治法实现归并排序的过程:
对于每个划分的排序顺序可以看成图的后序遍历
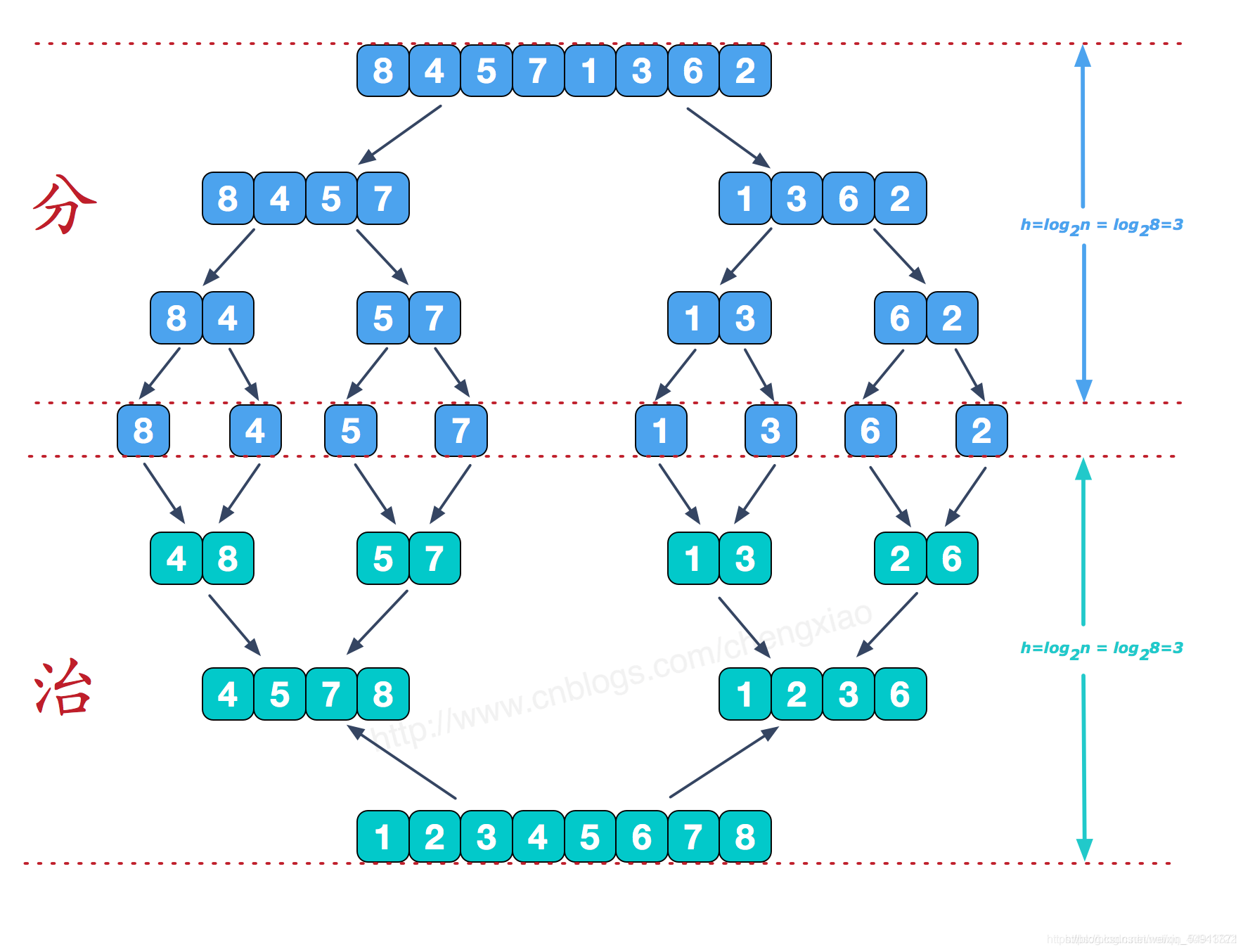
可以看到,我们将原序列不断进行二分,直至只有一个元素,得到n个只含有一个元素的序列,再将这n个需序列不断地两两合并,最终得到一个有序的序列。
这个过程中,合并是实现排序的关键过程,我们是这样实现合并相邻子序列的:
我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
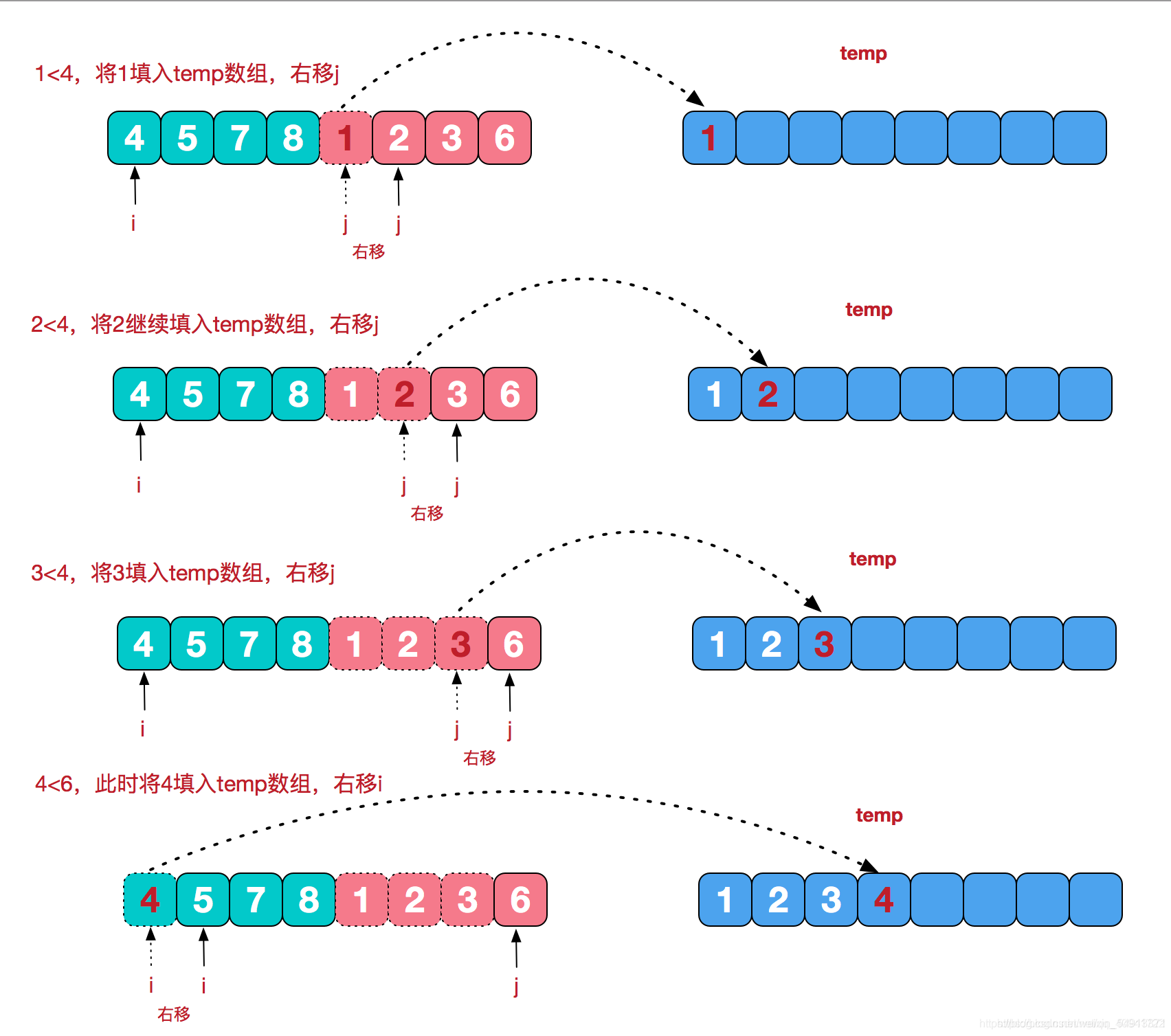
这个过程很简单,只要比较两个数列的第一个数,谁小就先取谁,取了后就在对应数列中删除这个数。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可
三、代码
#include<iostream>
using namespace std;
void MergeSortArr(int arr[],int left,int mid,int right){//该函数同于将两个有序列合并成一个有序列,同时当两个有序列都为同一个元素是一样可以处理
int i = left,j = mid + 1;//两个索引用来遍历两个有序列
int k=0;//k用来遍历暂存数组temp
int temp[right-left+1];//开一个数组暂时存放
while(i <=mid && j <= right){//对两个有序列进行遍历排序,有一个序列遍历完成结束循环
if(arr[i] < arr[j])
temp[k++] = arr[i++];
else
temp[k++] = arr[j++];
}
while(i <= mid){//将另外一个没有遍历完全的有序列全部插入到temp中
temp[k++] = arr[i++];
}
while(j <= right){
temp[k++] = arr[j++];
}
//!!这里需要注意循环的条件里面不能使用left因为left的值在改变
for(i = 0;i < k;i++)//将排好序的序列更新到目标数组中
arr[left++] = temp[i];
}
//递归方法
void MergeSort(int arr[],int left,int right){
if(left == right)//如果两个划分为同一元素,递归结束
return ;
int mid = (left + right) / 2;//对本个划分再次进行划分
MergeSort(arr, left, mid);//对左边的序列进行划分此条命令结束代表左边的序列已经有序
MergeSort(arr, mid+1, right);//对右边的序列进行划分此条命令结束代表右边的序列已经有序
MergeSortArr(arr, left, mid, right);//和并两个序列
}
//非递归方法
/*
非递归方法需要两个个索引
i表示每个划分个数
j表示每个划分第一个元素
三个遍历存放left mid right
*/
void MergeSort1(int arr[],int n){
int i,j;
int left,mid,right;
for(i=2; ;i *= 2){
for(j = 0;j < n;j += i){
left = j;
//当一个划分中的元素大于等于2个是mid不会出错,当只有一个元素时,right必定是错误的则会导致mid错误
mid = (j + j + i - 1) / 2 < n? (j + j + i - 1) / 2 : n-1;
right = (j + i -1) < n? (j + i -1) : n-1;
MergeSortArr(arr, left, mid, right);
}
if(i > n)
break;
}
}
int main(){
int arr[8] = {8, 4, 5, 7, 1, 3, 6, 2};
for(int i = 0;i < 8;i++)
cout<<arr[i]<<" ";
cout<<endl;
MergeSort(arr,0,7);
for(int i = 0;i < 8;i++)
cout<<arr[i]<<" ";
cout<<endl;
}