[C++知识库]C++主席树求第k小得数模板程序详解

#include<bits/stdc++.h>
#define reint register int
using namespace std;
int n,m;
inline void read(int &a) {  //快读
	int x(0),y(1);
	char c=getchar();
	while(c<'0'||c>'9') {
		if(c=='-')y=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9') {
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	a=x*y;
	return;
}
inline void write(int x) {  //快输
	if(x<0) {
		putchar('-');
		x=-x;
		write(x);
	} else {
		if(x>9) {
			write(x/10);
		}
		putchar(x%10+'0');
	}
}

int s[200005],p,root[200005],top,s_[200005],q,k;
struct nod {
	int l,r,val;
} tree[100000005];

int update(int node,int l,int r) {   //建1~n的树
	int new_node=++top;   //新建节点
	tree[new_node]=tree[node];  //新增节点，继承上一个节点
	tree[new_node].val++;  //因为是通过update增加一棵树，且每次增加都会有一个新的数进来，因此权值必+1
	if(l==r) {     //叶子节点
		return new_node;  //返回节点下标
	} else {
		int mid=(l+r)>>1;   //中间值
		if(p<=mid) {   //如果
			tree[new_node].l=update(tree[new_node].l,l,mid);  //看更新的节点在哪一颗子树，在左边就更新左子树
		} else {
			tree[new_node].r=update(tree[new_node].r,mid+1,r);  //否则右子树
		}
	}
	return new_node;  //返回新节点下标，用来给上一个节点记录子树下标
}


void build(int &node,int l,int r) {   //新建空树
	node=++top;   //新建节点下标
	tree[node].val=0;   //权值初始化
	if(l==r) {  //子节点
		return;   //返回
	}
	int mid=(l+r)>>1;   //中间值
	build(tree[node].l,l,mid);   //建左节点
	build(tree[node].r,mid+1,r);    //建右节点
}

int query(int lnode,int rnode,int l,int r,int k) {   //查询，解释在代码下面
	if(l==r) {
		return l;
	} else {
		int x=tree[tree[rnode].l].val-tree[tree[lnode].l].val;  
		int mid=(l+r)>>1;
		if(k<=x)
			return query(tree[lnode].l,tree[rnode].l,l,mid,k);
		else
			return query(tree[lnode].r,tree[rnode].r,mid+1,r,k-x);
	}
}

int main() {
	reint i,l,r;
	scanf("%d",&n);
	scanf("%d",&m);
	for(i=1; i<=n; ++i) {
		read(s[i]);
		s_[i]=s[i]; //复制，用来离散化
	}
	sort(s_+1,s_+n+1);   //离散化数组排序
	q=unique(s_+1,s_+n+1)-s_-1;   //s_数组去重
	build(root[0],1,q);  //用0根建议一颗空树
	for(i=1; i<=n; ++i) {
		p=lower_bound(s_+1,s_+1+q,s[i])-s_;  //此函数相当于在1~q的范围里找到第一个大于等于s[i]的数的下标（也就是s[i]应该在的位置），然后记录在p里
		root[i]=update(root[i-1],1,q);  //新增根节点，然后把s[i]加进数组
	}
	for(i=1; i<=m; ++i) {
		read(l);read(r);read(k);
		write(s_[query(root[l-1],root[r],1,q,k)]);  //query用来查找第k小的下标，然后用数组输出下标做代表的数
		putchar('\n');
	}
}

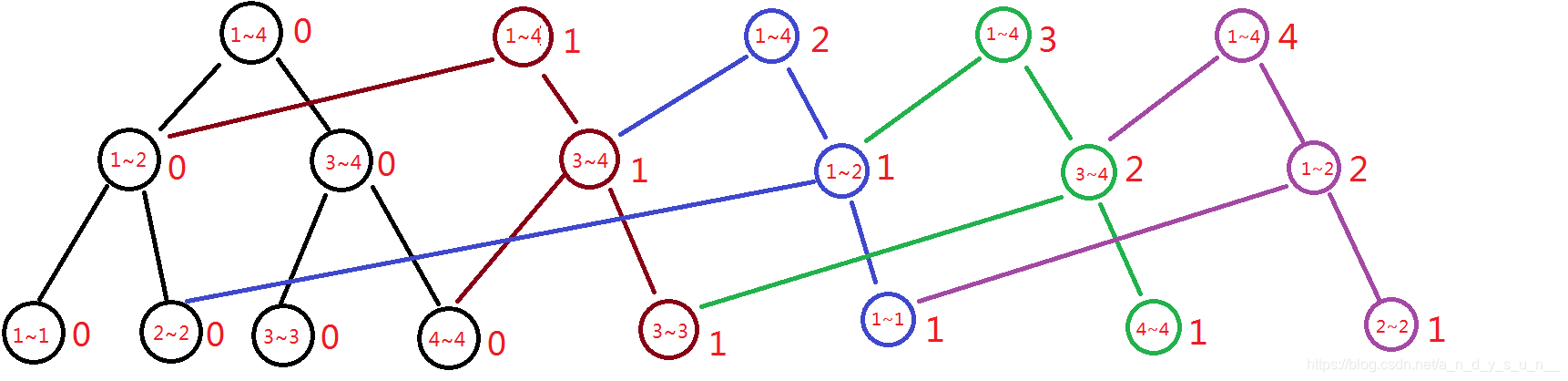
查询第k小的方法解释：

$${}^{{}^{图片来源}}$$

假设我们要查1 ~ 3中第2大的值，我们要先确定查找的范围，也就是从第零个根（红色）到第三个根（绿色）的第2大，然后从做左到右按顺序查，先找到3的左节点和一的左节点，看这两个节点之间有几个在1 ~ 3之间（也就是用左子节点的值减去右子节点的值（因为节点存的就是数的个数）），显然减完后只有1，也就是这个区间只有一个数，然而我们要找第二小，因此要找右子节点，又因为我们是按数的顺序建的树，所以在左子节点那里面的一个数一定小于右子节点的所有数，所以我们只需要在右子节点里面找到第2-1大的数，就是整个区间第2大的数，后面的按这个顺序推下去，找到根节点就返回下标，就完成了查询操作。

转载请注明出处，作者：Andysun06