[C++知识库]浮点类型在内存中的存取(C语言)

浮点数在内存中的存入

先给大家看一段代码

int main()
{
	int a = 9;
	float b = 9.0;
	printf("%d\n", a);
	printf("%f", b);

	return 0;
}

输出结果

可以看到虽然是一样的数字，但是整型和浮点型在内存中存储方式有所不同

由此可见int类型和浮点类型在内存中的存储方式是不同的

任意一个浮点数都可以表示成 (-1)^S * M * 2^E

其中S代表符号(1表示负数,0表示正数)，M代表有效数字(1<=M<2)，E代表指数（无符号数）。

例如: 就拿刚刚的9.0来说,它的符号位就是0；它的有效数字位二进制为1001.0，相当于1.001 * 2³;所以可以得出S=0,M=1.001,E=3;
对于32位的浮点数，最高位是符号位S,接着8位是指数E，剩下的23位是有效数字M
如图

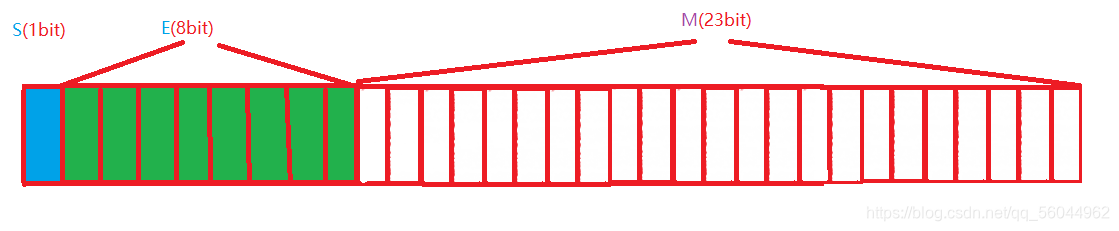
而对于64位的浮点数,最高位是也是符号位，接下来的11位是指数E,最后还剩下52位是有效数字M
如图:

在这里还有一些特别的规定
M
因为1<=M<2,其实M就一定会是1.xxxxx的形式,
所以保存M的时候，就舍去了这个开头的**“1”**，从而可以保存更大的数字.
E
其实很多人就发现了，那E为负数怎么表示呢
其实
浮点就用下面的规则表示，用E的计算值减去127（或者1023)，得到真实值，再将
当然，还有一些比较特殊的情况
E为全0
试想一下，当一个指数位为0时，那他的计算值就是-127（或者-1023），一个数的-127(或-1023）次方将会非常小（接近0），所以此时有效数字M之前不在加上舍去的“1”，这样就可以表示0。
E为全1
和上面一样，那个数字就会十分的大，所以可以表示无穷大或无穷小（取决符号位）。

聪明的读者想必就已经知道之前的问题的答案了吧 😃

9.0 的二进制表示为 1001.0 ->1.001 * 2³

S=0 , E=3+127 , M=1.001

内存中的9.0

0 10000010 001 0000 0000 0000 0000 0000

转化为16进制放在内存里就是

00 00 10 41

浮点数在内存中的取出

int main()
{
	float a = 9.0f;
	int b = *(int*)&a;
	printf("%d ", b);

	printf("%f", a);


	return 0;
}

这段代码输出结果并不是 9 9.0000000
而是

然后我们通过调试可以看到
a在内存中的数据为

b在内存中的数据为

可以看到内存中的数据相同，但是为什么输出的数据却天差地别呢?
就是因为取出的方式不同
由上文可知
浮点数是由符号，有效数字，指数部分组成，所以去除方式也有所差异
也可以知道9.0在内存中是这样的

0 10000010 001 0000 0000 0000 0000 0000

那么这样的数字按照整数类型会是什么结果？
计算器计算的结果

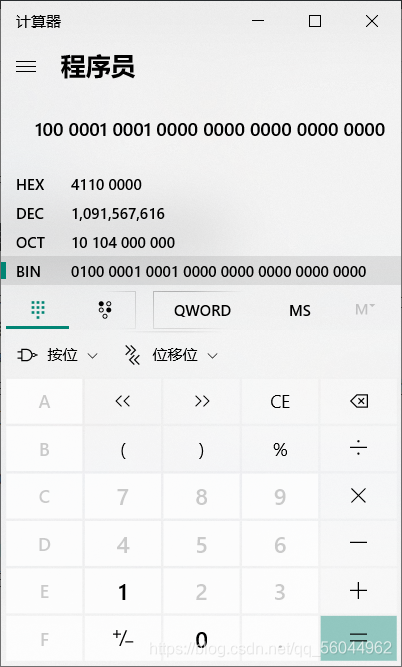
可以看到和上面的结果一致。

关于浮点数的存和取就说到这里，如果有意见或建议可以在评论区留言，拜拜 😃