[C++知识库]二叉排序树的删除，完成bilibili懒猫老师作业，c/c++描述

??此前已经写了一篇文章，介绍了二叉排序树的插入，建立，查找，和删除。地址如下：
https://blog.csdn.net/zhangzhangkeji/article/details/119681803
??但看过bilibili懒猫老师的视频后，才对书里的递归方法删除节点的程序有了理解。所以，本程序里重写了BST的删除算法。
??BST（binary sort tree ）的删除节点后，仍应该保持BST的排序性质不变，即左子节点的键值 < 根节点的键值 < 右子节点的键值。所以删除，更像是节点的替换操作。
??懒猫老师的讲解视频地址在这里：
懒猫老师-数据结构-(58)二叉排序树的删除(二叉查找树)_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1EK4y1e7UY
??讲解的非常好。不用我再多说一句了。
??作为总结，再说几点自己的体会。
??1 参数里的引用操作&，从实参开始，到递归里传递到的每一个形参，指的都是同一个变量。对被调函数里形参值的修改，相当于对主调函数里实参的修改。从而可以在主调函数里使用改动后的实参值。此符号来自c++，c里没有，但确实好用。
??2 被删节点是否为根节点，被删节点的左子树的最大节点是否为被删节点的左子节点。情况复杂，但视频程序里处理的非常巧妙，言简意赅。
??3 对于把BST转换成双向链表，且链表里元素顺序符合BST的中序输出，树里节点的ptLeftChild和ptRightChild域改意义成双向链表里元素的前指针和后指针域。老师要求不借助其余节点。我思来想去，借助于一个指针数组，BST的中序遍历时，把节点的地址依次存入数组，再根据数组里节点的排列顺序，依次修改其指针域，至此，原BST树已经被摧毁的啥都不剩了。最后输出链表的双向排列，以检验其正确性。该题目的要求跟中序线索化很像，但也不同，线索化后仍然是Tree，这里成了真正的双向链表。
??函数deleteKey：删除关键字值等于key的节点。其采用递归方法找到对应的被删节点，具体删除过程另由函数完成。
??函数deletePt ： 删除给定指针指向的节点。此函数浓缩了大智慧。看了老师的视频才学会。该函数综合考虑了被删节点是否为根节点和被删节点的左子树的最大节点是否为被删节点的左子节点等各种情况。
??函数transferTreeToDoubleLinkedList：把BST树转换成双向链表。借助了一个数组，转换后，节点间符合关键字递增递减的排序。
全部代码如下，先是main函数所在源文件：

#include<iostream>
using namespace std;

struct Node {
	int data;
	Node* ptLeftChild;
	Node* ptRightChild;
};

extern void insertBST(Node * & root,int data);
extern void searchBSTRecursion(Node*& root, int data,int path[],int length);
extern void searchBSTNoRecursion(Node*& root, int data,int path[],int length);
extern void inOrderTraverse(Node*& root);
extern void displayBST(Node*& root);
extern bool deleteKey(Node*& root,int key);
extern void deletePt(Node *& ptDelete);
extern void transferTreeToDoubleLinkedList(Node * & root,Node * pts[],int& length);

int main() {
	int a[] = {4,9,0,1,8,6,3,5,2,7},length = 10;
	Node* root = NULL;

	for (int i = 0; i < length; i++)
		insertBST(root,a[i]);

	cout << "middle order traverse : ";
	inOrderTraverse(root);

	cout<<endl<<"逗号表达式表示该二叉树 ：";
	displayBST(root);

	int path[20];
	cout << endl<<endl;
	searchBSTNoRecursion(root,6,path,0);
	searchBSTNoRecursion(root,11,path, 0);
	
	cout << endl;
	searchBSTRecursion(root,11,path,0);
	searchBSTRecursion(root, 6, path, 0);

	cout << endl;
	int key = 4;
	if (deleteKey(root, key)) {
		cout << "delete "<<key<<" : ";
		inOrderTraverse(root);
		cout << endl;
	}
	else
		cout << "list can not delete " << key << " ,list does not include this data ." << endl;

	key = 6;
	if (deleteKey(root, key)) {
		cout << "delete " << key << " : ";
		inOrderTraverse(root);
		cout << endl;
	}
	else
		cout << "list can not delete " << key << " ,list does not include this data ." << endl;

	key = 5;
	if (deleteKey(root, key)) {
		cout << "delete " << key << " : ";
		inOrderTraverse(root);
		cout << endl;
	}
	else
		cout << "list can not delete " << key << " ,list does not include this data ." << endl;

	key = 99;
	if (deleteKey(root, key)) {
		cout << "delete " << key << " : ";
		inOrderTraverse(root);
		cout << endl;
	}
	else
		cout << "list can not delete " << key << " ,list does not include this data ." << endl;

	Node* pts[10];
	int lengthB = 0;
	transferTreeToDoubleLinkedList(root,pts,lengthB);

	pts[0]->ptLeftChild = NULL;
	pts[lengthB - 1]->ptRightChild = NULL;
	for (int i = 0; i < lengthB - 1; i++) {
		pts[i]->ptRightChild = pts[i + 1];
		pts[i + 1]->ptLeftChild = pts[i];
	}
	root = pts[0];

	cout << endl << "double link list : ";
	Node* pt = root;
	while (pt->ptRightChild != NULL) {
		cout << pt->data << "  ";
		pt = pt->ptRightChild;
	}
	while (pt != NULL) {
		cout << pt->data << "  ";
		pt = pt->ptLeftChild;
	}
	
	return 0;
}

接着是各函数所在源文件：

#include<iostream>
using namespace std;

struct Node {
	int data;
	Node* ptLeftChild;
	Node* ptRightChild;
};

void insertBST(Node*& root, int data) {
	if (root == NULL) {
		root = new Node;
		root->data = data;
		root->ptLeftChild = root->ptRightChild = NULL;
		return;
	}

	if (root->data > data)
		insertBST(root->ptLeftChild, data);
	else if (root->data < data)
		insertBST(root->ptRightChild,data);
	else 
		cout << "key " <<data<<" repeated ! " << endl;
}

void searchBSTRecursion(Node*& root, int data,int path[],int length) {
	if (root == NULL) {
		cout << "recursion,list do not include this data : "<<data << endl;
		return;
	}

	if (root->data > data) {
		path[length] = root->data;
		length++;
		searchBSTRecursion(root->ptLeftChild, data, path, length);
	}
	else if (root->data < data) {
		path[length] = root->data;
		length++;
		searchBSTRecursion(root->ptRightChild,data,path,length);
	}
	else {
		cout << "recursion,path from root to " << data << " : ";
		for (int i = 0; i < length; i++)
			cout << path[i] << " ";
		cout << data << endl;
	}
}

void searchBSTNoRecursion(Node*& root, int data,int path[],int length) {
	Node* pt = root;
	while (pt != NULL) 
		if (pt->data > data) {
			path[length] = pt->data;
			length++;
			pt = pt->ptLeftChild;
		}
		else if (pt->data < data) {
			path[length] = pt->data;
			length++;
			pt = pt->ptRightChild;
		}
		else {
			cout << "no recursion ,from root to " << data << " : ";
			for (int i = 0; i < length; i++)
				cout << path[i] << ' ';
			cout << data << endl;
			return;
		}
	
	cout << "no recursion ,list has no this data : " << data << endl;
}

void inOrderTraverse(Node*& root) {
	if (root == NULL)
		return;

	inOrderTraverse(root->ptLeftChild);
	cout << root->data << ' ';
	inOrderTraverse(root->ptRightChild);
}

void displayBST(Node*& root) {
	if (root == NULL)
		return;

	cout << root->data;
	if (root->ptLeftChild != NULL || root->ptRightChild != NULL) {
		cout << '(';
		displayBST(root->ptLeftChild);
		
		if (root->ptRightChild != NULL) {
			cout << ',';
			displayBST(root->ptRightChild);
		}

		cout << ')';
	}
}

bool deleteKey(Node*& root, int key) {
	void deletePt(Node * &ptDelete);

	if (root == NULL)
		return false;

	if (root->data > key)
		return deleteKey(root->ptLeftChild, key);
	else if (root->data < key)
		return deleteKey(root->ptRightChild, key);
	else
		deletePt(root);

	return true;
}

void deletePt(Node* & ptDelete) {
	Node* ptTemp;
	if (ptDelete->ptLeftChild == NULL && ptDelete->ptRightChild == NULL) {
		ptTemp = ptDelete;
		ptDelete = NULL;
		delete ptTemp;
	}
	else if (ptDelete->ptLeftChild == NULL) {
		ptTemp = ptDelete;
		ptDelete = ptDelete->ptRightChild;
		delete ptTemp;
	}
	else if (ptDelete->ptRightChild == NULL) {
		ptTemp = ptDelete;
		ptDelete = ptDelete->ptLeftChild;
		delete ptTemp;
	}
	else {
		Node* ptParentTemp = ptDelete;
		ptTemp = ptDelete->ptLeftChild;
	
		while (ptTemp->ptRightChild != NULL) {
			ptParentTemp = ptTemp;
			ptTemp = ptTemp->ptRightChild;
		}
	
		//情况1 ： root = ptDelete = ptParentTemp , ptTemp = root.ptLeftChild
		//情况2 ： root = ptDelete != ptParentTemp , ptTemp = ptParentTemp.ptLeftChild
		//情况3 ： root != ptDelete = ptParentTemp , ptTemp = ptDelete.ptLeftChild
		//情况4 ： root != ptDelete != ptParentTemp , ptTemp = ptParentTemp.ptLeftChild
		ptDelete->data = ptTemp->data;
		if (ptParentTemp == ptDelete)  //左子树的最大节点是否是左子树的根节点
			ptDelete->ptLeftChild = ptTemp->ptLeftChild;
		else
			ptParentTemp->ptRightChild = ptTemp->ptLeftChild;
		
		delete ptTemp;
	}
}

void transferTreeToDoubleLinkedList(Node*& root, Node* pts[], int &length) {
	if (root == NULL)
		return;

	transferTreeToDoubleLinkedList(root->ptLeftChild,pts,length);

	pts[length] = root;
	length++;

	transferTreeToDoubleLinkedList(root->ptRightChild,pts,length);
}

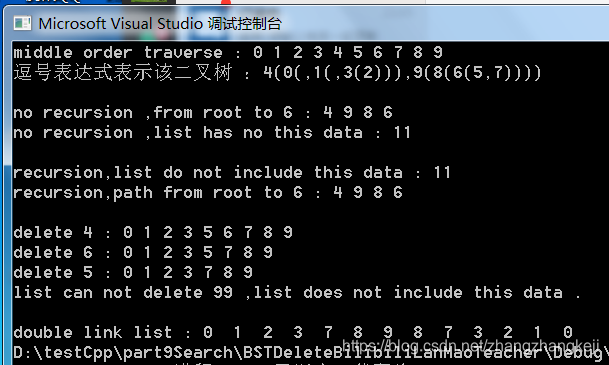
测试结果及对应的树如下：


谢谢阅读。