前言

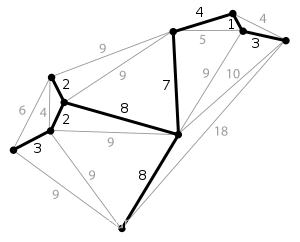
摘自wiki

最小生成树其实是最小权重生成树的简称。

一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。广义上而言，对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。

以有线电视电缆的架设为例，若只能沿着街道布线，则以街道为边，而路口为顶点，其中必然有一最小生成树能使布线成本最低。

以上选自wiki。

算法详情

创建一个优先队列。先选取第一个点，作为起点，将与其连接的所有边加入优先队列。
取队列中权重最小的边，若另一端没有被访问过，则加入树中，并将该节点连接的所有边都放入优先队列。
重复以上工作，直到访问完所有点。

代码

#include <algorithm>
#include <memory>
#include <vector>
#include <utility>
#include <Eigen/Dense>
#include <queue>

class MinimumSpinningTree
{
public:
  std::vector<std::vector<std::size_t>> getTree(Eigen::MatrixXd graph)
  {
    generateMinimumSpinningTree(graph);
    return adjacent_list_;
  }

private:
  void generateMinimumSpinningTree(Eigen::MatrixXd graph);

  std::vector<std::vector<std::size_t>> adjacent_list_;
  std::unique_ptr<GridMap2D> grid_map_ptr_;
  using EdgeWithVertex =
      std::pair<double, std::pair<std::size_t, std::size_t>>;  // <edge_length, <start_vertex, end_vertex>>

  static bool edgePriorityComparator(const EdgeWithVertex& lhs, const EdgeWithVertex& rhs)
  {
    return lhs.first > rhs.first;
  }

  using DistancePriorityQueue =
      std::priority_queue<EdgeWithVertex, std::vector<EdgeWithVertex>, decltype(edgePriorityComparator)*>;
};


void MinimumSpinningTree::generateMinimumSpinningTree(Eigen::MatrixXd graph)
{
  std::size_t node_num = graph.rows();
  adjacent_list_.clear();
  adjacent_list_.resize(node_num);

  std::vector<bool> added_nodes(node_num, false);
  std::size_t nodes_remained_num = graph.rows();

  DistancePriorityQueue candidate_edges{ edgePriorityComparator };

  for (std::size_t i = 1; i < graph.rows(); ++i)
  {
    candidate_edges.push({ graph(0, i), { 0, i } });
  }
  added_nodes[0] = true;
  nodes_remained_num--;

  while (nodes_remained_num)
  {
    auto min_edge = candidate_edges.top().second;
    candidate_edges.pop();
    if (added_nodes[min_edge.second])
    {
      continue;
    }

    added_nodes[min_edge.second] = true;
    nodes_remained_num--;
    adjacent_list_[min_edge.first].push_back(min_edge.second);
    adjacent_list_[min_edge.second].push_back(min_edge.first);
    for (std::size_t i = 1; i < graph.rows(); ++i)
    {
      if (i == min_edge.second)
      {
        continue;
      }
      candidate_edges.push({ graph(i, min_edge.second), { min_edge.second, i } });
    }
  }
}