??相信每一位格物致知认真细致的学生,都不会放过这个知识点的掌握。而不是去死记硬背。这也是我们未来学的更多,做的更好的保证。
??给个链接,这篇文章分析的就很好:
关于B树的思考:m阶B树的非根非叶节点为什么要至少为ceil(m/2)个孩子?_oxygen’s blog-CSDN博客
https://blog.csdn.net/oxygen0106/article/details/40262829
??接着写些我自己的理解。
??采用B树,而不是二叉树,是为了建立大节点,让每个节点包含的数据更多,包含更多的元素,更多的指针。从而减小树的高度。这是为了优化对磁盘数据的访问而设计的数据结构,而非对主内存。因为电脑对外磁盘的访问速度慢,远比对主内存的访问慢,但每次从磁盘的块区读取的数据也多。如果树里每个节点对应磁盘的一个块区。那么合理组织树的结构,尽最大可能减少树的高度。将有利于提高对磁盘数据的访问速度。

??磁盘上数据必须用一个三维地址唯一标示:柱面号、盘面号、块号(磁道上的盘块)。
??设树里节点的最大指针数为 m ,则树里节点的最小指针数为ceil(m/2) - 1 。
??若 m = 9 ,则节点最大元素数为8,最小指针数为 5 ,最少元素数为 4 。
??若m = 10,则节点最大元素数为9,最小指针数为 5 ,最少元素数为 4 。
??观察可以得到:在建立B树,往B树里插入元素时,一个最大节点刚好可以拆分成两个最小节点,为其父母节点多提供一个元素,一个指针的位置。若父母节点已经是最大节点,则父母节点再拆分成两个最小节点,这两个小节点对上提供两个指针,所以新建爷爷奶奶节点,接受这两个指针,结果是树的高度加一。这也是合理的,因为往树里插入元素过多,必然导致树的高度增加。
举例如图:
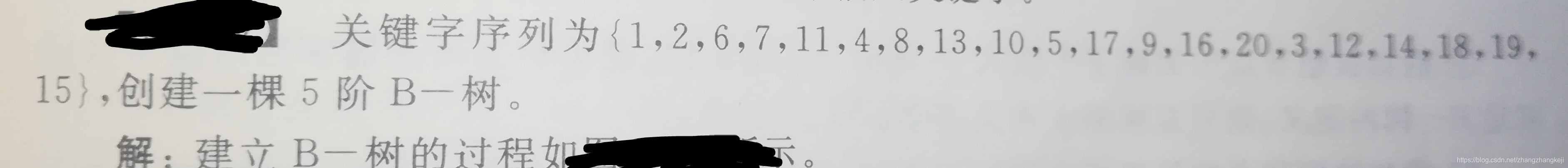

??同理,从B树里删除元素时,若被删元素所在节点是最小节点,其兄弟节点也是最小节点,父母节点是最小根节点(一元素和俩指针),则可以删除元素后,合并这三个节点,形成一个大节点,同时降低了树的高度。其余复杂情况可以以此类推。规定ceil(m / 2) - 1 这个数就是为了俩最小节点合并成最大节点,一个最大节点拆分成俩最小节点时用的。
??所以如此规定,可以简化程序的处理,算法更为简单。同时,也规定了最小指针数的限度,尽最大可能压缩树的高度。使插入和删除时也有规律可循。做到了程序各方面性能最大程度的均衡和优化。
再提供删除节点时的图:

谢谢阅读