[C++知识库] 递归入门（C语言实现）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> C++知识库 -> 递归入门（C语言实现） -> 正文阅读

[C++知识库]递归入门（C语言实现）

递归：将一个复杂的问题简单化。

讲递归之前，我们先回忆一下函数。

函数：单入口，单出口。

例1：求小明在一段时间内跑的步数。

假设有个函数XiaomingSteps(time1,time2)能独立完成这个事情，我们就可以这样写：

#include<stdio.h>

void main()

{

???? scanf("%d %d",&time1,&time2);

???? printf("%d",XiaomingSteps(time1,time2));

???? return 0;

}

这样，我们就我们求出了小明在time1到time2这段时间内跑的步数。

如果所有的题目都有一个特定的函数可以直接求出答案，那么我们用相应的函数就能解决所有的题目。

如果这个函数是要自己调用自己。

例2：假如你不知道自己多大，那么你就要问去年的自己：“你多大了？”去年的你说：“我不知道。”那么去年的你就要去问前年的你，前年的你还是不知道，又去问大前年的你……

也就是：

你→去年的你→前年的你→大前年的你→……

能不能问出个结果呢？

答案是不能，因为这永远没有终止条件。

我们再看一个例子：

例3：假如今年你18岁，今年挣了1000元钱（也可能是压岁钱）。问你这一生，也就是0岁到18岁，总共挣了多少钱？

18岁的你问17岁的你，17岁的你回答：“我算出来了，0到18岁总共挣了 1000元 + 16岁的我挣的钱。”

17岁的你问16岁的你，16岁的你回答：“我算出来了，0到18岁我总共挣了 1000元 + 15岁的我挣的钱。”

这样一直问下去，直到1岁的你问0岁的你，1岁的你回答：“我算出来了，0到18岁我总共挣了?1000元 + 0岁的我挣的钱。”

0岁的你说：“我在0岁时挣了10000元（刚出生时挣得的红包钱）。”

这个有没有结束的可能？

0岁——0岁之前还有可能挣钱吗？没有可能！因为0岁之前你还没有出生。

你在18岁的时候并没有关心17岁之前挣了多少钱，因为18岁的你坚信，去问17岁的你，就一定能得到一个值。

所以我们只需要做什么操作呢？

假设有一个函数age( )，age(18)表示你0到18岁总共挣的钱，age(17)表示你0到17岁总共挣的钱，age(16)表示你0到16岁总共挣的钱……以此类推，这里面就一个参数，因此比较容易实现。

#include<stdio.h>

int main()

{

???? printf("%d",age(18));

???? return 0;

}

但有人又会问，age( )是什么？没有人给出来，所以我们就只能自己写。

#include<stdio.h>

//age(18) = age(17) + 1000;

//age(17) = age(16) + 1000;

int age(int n)

{

???? printf("第%d次调用\n",n);

???? return age(n-1) + 1000;

}



int main()

{

???? printf("%d",age(18));

???? return 0;

}

一直到溢出了才结束。

对于这种调用，一定要有退出条件。我们在age( )函数内加上退出条件，于是就有下面的一段代码：

#include<stdio.h>

//age(18) = age(17) + 1000;

//age(17) = age(16) + 1000;

int age(int n)

{

???? if(n <= 0)

????????? return 10000;

???? printf("第%d次调用\n",n);

????      return age(n-1) + 1000;

}



int main()

{

???? printf("%d",age(18));

???? return 0;

}

这时候，有人就会说：你这太慢了，还不如我口算快。别急，我们再看下面的几个例子，再进一步熟悉递归。

例4：求阶乘。

我们先求一下6的阶乘，将大概的框架先写出来：

#include<stdio.h>

//n = n * (n-1)!

int Factoricgal(int n)

{

???? return n * Factorical(n-1);

}



int main()

{

???? printf("%11d",Factorical(6));

???? return 0；

}

接着我们补上终止条件：

#include<stdio.h>

//n = n * (n-1)!

int Factoricgal(int n)

{

???? printf("第%d次\n",n);

???? if(n ==1 || n == 0)

????????? return 1;

???? return n * Factorical(n-1);

}



int main()

{

???? printf("%11d",Factorical(6));

???? return 0；

}

但是，当我们将主函数中的Factorical(6)换成Factorical(-6)时：

#include<stdio.h>

//n = n * (n-1)!

int Factoricgal(int n)

{

???? printf("第%d次\n",n);

???? if(n ==1 || n == 0)

????????? return 1;

???? return n * Factorical(n-1);

}



int main()

{

???? printf("%11d",Factorical(-6));

???? return 0；

}

我们发现，程序不对了。在上面的程序中，我们并没有考虑到负数的情况，这是许多程序设计竞赛中我们往往忽视的一个点。因此，程序还需要进行改动，应考虑到n小于零的情况：

#include<stdio.h>

//n = n * (n-1)!

int Factoricgal(int n)

{

???? printf("第%d次\n",n);

???? if(n ==1 || n == 0)

????????? return 1;

???? if(n < 0)

????????? return 0;

???? return n * Factorical(n-1);

}



int main()

{

???? printf("%11d",Factorical(-6));

???? return 0；

}

接下来，我们将主函数中的Factorical(-6)换成Factorical(20)：

#include<stdio.h>

//n = n * (n-1)!

int Factoricgal(int n)

{

???? printf("第%d次\n",n);

???? if(n ==1 || n == 0)

????????? return 1;

???? if(n < 0)

????????? return 0;

???? return n * Factorical(n-1);

}



int main()

{

???? printf("%11d",Factorical(20));

???? return 0；

}

我们发现，程序又出现了问题。因为int类型最大到2^32=4,294,967,296，而long long类型最大到2^64=18,446,744,073,709,551,616。

此时，我们只要将int类型改为long long类型即可：

#include<stdio.h>

//n = n * (n-1)!

long long Factoricgal(int n)

{

???? printf("第%d次\n",n);

???? if(n ==1 || n == 0)

????????? return 1;

???? if(n < 0)

????????? return 0;

???? return n * Factorical(n-1);

}



int main()

{

???? printf("%11d",Factorical(6));

???? return 0；

}

此题有两个需要考虑的细节：

出现负数；
数据大小大于2^32。

我们要注意的是：

递归要怎么才往下走；
递归结束的条件；
数据的范围。

例5：小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!
站在台阶前，他突然又想着一个问题：
如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？

输出格式：
输出一个整数

为了便于理解，我们先考虑礼堂前只有4级台阶的情况。

在只有4级台阶的情况下，小明迈上一步（也就是1个或2个台阶），只可能到达第3级或第2级台阶。

如果在第4级台阶时，小明选择一步迈上了1个台阶，那么他将到达的是第3级台阶；小明在3级台阶的情况下，小明再迈上一步（也就是1个或2个台阶），只可能到达第2级或第1级台阶。

如果在第3级台阶时，小明选择一步迈上了1个台阶，那么他将到达的是第2级台阶；小明在2级台阶的情况下，小明再迈上一步（也就是1个或2个台阶），只可能到达第1级或第0级台阶……

这样说起来未免有些繁琐，我们不妨用一张图来简要表明上述过程：

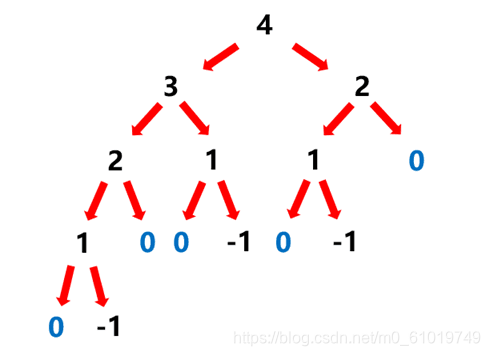
?经过上面的分析，我们不难得到一个大体的程序框架：

#include<stdio.h>

int step(int n)

{

????

}



int main()

{

???? printf("%d",step(4));

???? return 0;

}

如果小明所处的台阶数是n，那么接下来会出现两种调用：

小明一步迈1个台阶；
小明一步迈2个台阶。

于是就有：

#include<stdio.h>

int step(int n)

{

???? return step(n-1) + step(n-2);

}



int main()

{

???? printf("%d",step(4));

???? return 0;

}

当然，不能忘记终止条件：

#include<stdio.h>

int step(int n)

{

???? if(n == 0)

????????? return 1;

???? return step(n-1) + step(n-2);

}



int main()

{

???? printf("%d",step(4));

???? return 0;

}

与前面的例4一致，我们应考虑到n<0的情况，注意保护程序：

#include<stdio.h>

int step(int n)

{

???? if(n == 0)

????????? return 1;

???? if(n < 0)

????????? return 0;

???? return step(n - 1) + step(n - 2);

}



int main()

{

???? printf("%d",step(4));

???? return 0;

}

现在，我们还有一个问题：我们怎么判断小明走的是偶数步呢？

我们定义一个变量num，代表小明所走的步数。初值是没有迈步，num的初值就设为0，每迈一步就使num+1。也就是每朝下调用一次，步数就加上1。这就涉及到二维的递归。

当n==0时，我们就能以num的奇偶性，来判断小明是否走的是偶数步。如果当n==0时，小明迈的是偶数步，我们就认为这种方案是可行的；反之小明迈的是奇数步，我们就认为这种方案是不可行的。

于是我们看到，现在递归的参数不仅仅是计算小明所在的台阶数，还能计算小明迈出的步数。代码如下：

#include<stdio.h>

int step(int n)

{

???? if(n == 0)

???? {

????????? if(num%2==0)

?????????????? return 1;

????????? else

?????????????? return 0;

???? }

???? if(n < 0)

????????? return 0;

???? return step(n-1,num+1) + step(n-2,num+1);

}



int main()

{

???? printf("%d",step(4));

???? return 0;

}

最后，求39级台阶，将“4”改为“39”即可：

#include<stdio.h>

int step(int n)

{

???? if(n == 0)

???? {

????????? if(num%2==0)

?????????????? return 1;

????????? else

?????????????? return 0;

???? }

???? if(n < 0)

????????? return 0;

???? return step(n-1,num+1) + step(n-2,num+1);

}



int main()

{

???? printf("%d",step(39));

???? return 0;

}

这一题递归展开的层数正好合适，不算太大。一般来说，我们使用递归时，要尽量控制递归展开的层数在6层以内，否则程序会有爆掉的风险！

接下来，我们讨论关于递归变形的调用。

例6：斐波那契数列

（注：斐波那契数列是一组第一位和第二位为1，从第三位开始，后一位是前两位和的一组递增数列，例如：0、1、1、2、3、5、8、13、21、34、55......）

?根据斐波那契数列的含义，我们利用数学知识能够很快写出它的函数表达式：

现在我们来简单分析一下上面写出的函数表达式：

函数中有一个参数n，在调用时出现两个，分别是f(n-1)和f(n-2)；

退出条件是：f(n) = 1,0≤n≤1；

防止错误条件：（其实也就是退出条件，但这是不可赋值的）：f(n) = 0,n<0。

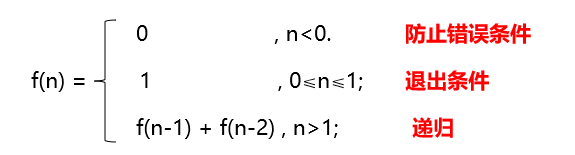
?易得：

#include<stdio.h>

int Fab(int n)

{

???? if(n==0 || n==1)

????????? return 1;

???? if(n<0)

????????? return 0;

???? return Fab(n-1) + Fab(n-2);

}



int main(void)

{

???? scanf("%d",&a)

???? printf("%d",Fab(a));

???? return 0;

}

例7：倒序输出一个正整数。

例如给出正整数12345，希望以各位数的逆序形式输出，即输出54321。

如果我们不用递归，则我们可以这样写：

#include<stdio.h>



int main()

{

???? int a;

???? scanf("%d",&a);

???? while(a != 0)

???? {

????????? printf("%d\t",a%10);

????????? a = a / 10;

???? }

???? return 0;

}

输出结果为：

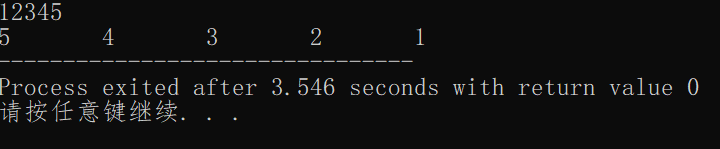
那如果输入的是负数呢？

显然，输入负数时，逆序输出的每一位前都带有负号，这是不符合题目的要求的。于是我们在程序中加上遇到负数时的情况：

#include<stdio.h>



int main()

{

???? int a;

???? scanf("%d",&a);

???? if(a<0)

???? {

????????? a = -a;

????????? printf("-");

???? }


???? while(a != 0)

???? {

????????? printf("%d\t",a%10);

????????? a = a / 10;

???? }

???? return 0;

}

这样，我们也能顺利地完成负数的逆序输出了。

程序补充到现在，我们能确保是万无一失的吗？在刚刚的讨论中，我们先考虑到了正数，后来又补充了负数的情况，可是还有一个数我们没有考虑到，那就是0：

#include<stdio.h>



int main()

{

???? int a;

???? scanf("%d",&a);

???? if(a<0)

???? {

????????? a = -a;

????????? printf("-");

???? }

     else if(a == 0)

???? {

????????? printf("0");

???? }

???? while(a != 0)

???? {

????????? printf("%d\t",a%10);

????????? a = a / 10;

???? }

???? return 0;

}

在刚刚的讨论中，我们将数字的最后一位先取出来输出，再将其去掉，循环往复，就能实现数字的逆序输出。

根据这个原理，我们再利用递归来做：

我们可以写一个函数BackOut( )，其目的正是如上面所述：将数字a的最后一位先取出来输出，再将其去掉，并循环往复。其中，注意其中止条件：a == 0。代码如下：

#include<stdio.h>

void BackOut(int a)

{

???? if(a == 0)

????????? return;

???? printf("%d\t",a%10);

???? BackOut(a/10);

}

int main()

{

???? int a;

???? scanf("%d",&a);

???? if(a<0)

???? {

????????? a = -a;

????????? printf("-");

???? }

???? else if(a == 0)

???? {

????????? printf("0");

???? }

???? BackOut(a);

???? return 0;

}

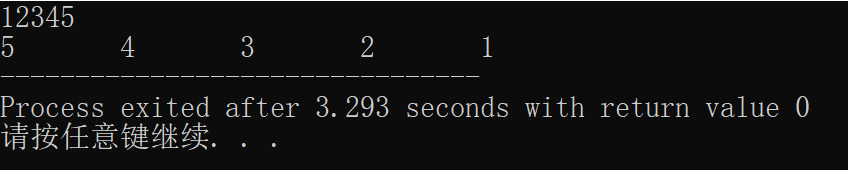
?很明显，在上面的程序中，我们先显示最后一位数字，再将其去掉，然后对剩下的数进行调用。

例如：12345

显示数字5---->调用1234---->

显示数字4---->调用123---->

显示数字3---->调用12---->

显示数字2---->调用1---->

显示数字1---->调用0---->触发中止条件

?这就是显示后调用。

?如果我们尝试一下调用后显示呢？

#include<stdio.h>

void BackOut(int a)

{

???? if(a == 0)

????????? return;

     BackOut(a/10);

???? printf("%d\t",a%10);?? 

}

int main()

{

???? int a;

???? scanf("%d",&a);

???? if(a<0)

???? {

????????? a = -a;

????????? printf("-");

???? }

???? else if(a == 0)

???? {

????????? printf("0");

???? }

???? BackOut(a);

???? return 0;

}

?我们发现，这时候变为正序输出了。

这就是两者的不同之处。

在这一题中，我们要思考：

1.怎么取每一位数字；

2.怎么调用任意长度的数字；

3.怎样才支持负数的逆序输出。（另外，0呢？）

例8：“李白街上走，提壶去买酒，遇店加一倍，见花喝一斗”，途中，遇见5次店，见了10次花，壶中原有2斗酒，最后刚好喝完酒，要求最后遇见的是花，求可能的情况有多少种？

首先，我们要想清楚这道题有几个参数。答案是三个，分别是：店、花、酒。

假如李白遇到的是店，那么就会有：店-1，花，酒*2；

假如李白遇到的是花，那么就会有：店，花-1，酒-1。

所以，我们就能写出大概的框架：

#include<stdio.h>

int Drink(int n,int m,int s)//n:店;m:花;s:酒.

{

???? return Drink(n-1,m,s*2) + Drink(n,m-1,s-1);

}

int main()

{

???? printf("%d",Drink(5,9,2));

???? return 0;

}

?接着我们补上终止条件：

#include<stdio.h>

int Drink(int n,int m,int s)//n:店;m:花;s:酒.

{

???? if(n == 0 && m == 0 && s == 1)

????????? return 1;

???? if(n<0) return 0;

???? if(m<0) return 0;

???? if(s<=0) return 0;

???? return Drink(n-1,m,s*2) + Drink(n,m-1,s-1);

}

int main()

{

???? printf("%d",Drink(5,9,2));

???? return 0;

}

?在终止条件这里，我们运用了一个小技巧：if(n == 0 && m == 0 && s == 1)，而我们输进去的参数值为Drink(5,9,2)，即遇见9次花，最后剩1斗酒，这样就能很好地避免判断。

总结：

要做好递归，就一定要做到“三个准”：

1.参数找准；

2.满足条件找准；

3.不可能条件找准。