[C++知识库] 对B树的插入删除理解和c/c++代码实践

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> C++知识库 -> 对B树的插入删除理解和c/c++代码实践 -> 正文阅读

[C++知识库]对B树的插入删除理解和c/c++代码实践

??B树没有那位猫老师的B树教学视频了，学起来好难啊。很多资料讲其原理，而不结合代码，不结合代码细节，终究是不到位的。课本里 i j k 太多，代码阅读不易于理解。搜罗各位前辈提供的资料，这里写下自己的总结。
??B树，也叫多路平衡查找树， multi - search banlance tree . 所以翻译为B树，对应B - Tree。本文约定节点的指针域为空（NULL）的节点为叶节点，同二叉树。B树里所有叶节点位于同一行。或者说叶节点的所有空指针位于同一行、同样的深度。这么规定也是为了最大程度降低树的高度。不允许个别叶节点的深度很深，而其他叶节点很浅。根节点的每棵子树的生长应该均衡，齐头并进。
??（1） B 树，是平衡树。跟二叉平衡树一样。平衡指的是，左边的关键字都小于右边的关键字。节点里元素的值，大于其左边指针指向的节点里元素的值，小于其右边指针指向的节点里元素的值。用类似于二叉树的中序遍历序列（左中右），也可以得到关键字的递增排列。
??（2）B树节点的程序描述：

struct Node {
	int numKeys;   //因为是定长数组，指示出节点里实际元素个数
	int keyArray[MAX];   //MAX比阶数要大
	Node* ptChildren[MAX];   //节点里的指针数组，指向其所有孩子节点
	Node* ptParent;   //指向该节点的父母节点。因为俩相邻子节点合并时需要知道其父母节点是谁
};

??节点里所有关键字由数组存储。节点里所有指针也由指针数组存储。这点跟二叉树是不同的。由于是足够大的定长数组，所以即便在插入节点的过程中，使某些节点的阶数超了最大阶数，也没事。接着再对大节点拆分就行。或者小于了最小节点的关键字数，也没事，合并相邻俩最小节点即可。
??（3）节点里的数据关系表示：
在这里插入图片描述

??（4）由图可见，节点里无论是哪个节点（根节点，叶节点或者分支节点），元素数目和指针数目始终保持着对应关系。按关键字大小交错交替布置。指针实际数目比关键字实际数目大 1 。这也是中序遍历平衡的要求。无论分支节点还是叶节点都符合这个关系。
??（5）由 4 可知，节点里添加一个元素（关键字），必然也要增加一个指针。元素有序排列，新添加指针的位置，仍然要符合平衡的要求：中序遍历关键字递增排列，加在新插入元素的相邻右侧（这是规定，插入位置和算法是对应的。按对称来讲，指针插入左侧好像也可以，课本是插入右侧）。每删除一个元素，必然要合并其左右相邻的两个指针。
??（6）这里也就容易理解为什么 m 阶 B 树的最少分支数是 ceil(m / 2) ,是为了插入元素时最大节点拆分成两个最小节点，删除元素时两个最小节点合并成一个最大节点。可见我的前几天一篇文章。关于B树的思考：m阶B树的非根非叶节点为什么要至少为ceil(m/2)个孩子？ c
https://blog.csdn.net/zhangzhangkeji/article/details/119739831
??（7）插入：无论哪种语言实现，都分为四个步骤：
??①查找树中是否已有该待插入元素，有则不再重复插入，由函数 searchTree 完成。
??②在合适的节点里插入该元素（即关键字），并插入一个指针。保证指针数比元素数大1。insertTree 。
??③若插入后节点太大，则拆分节点，节点里的元素和指针同时被拆分。完成所有指针域值的修改。split。
??④节点被拆分后，多出来一个元素和一个右兄弟节点。多出来的这个元素和对应右兄弟节点的指针，插入被拆节点的父母节点。插入位置，由关键字递增排列确定。函数insertNode。
??⑤若父母节点太大，超过阶数，则拆分父母节点。再把多出来的元素插入爷爷奶奶节点，直至根节点，如此循环。
??⑥若根节点被拆分，则生成一个新的根节点，newRoot。
?? 下面给出其流程图：
在这里插入图片描述

??（8）删除：关键字的删除分两大类：被删关键字在叶节点里或在分支节点里。被删关键字在分支节点里，则其是不能删除的（根节点也不例外，根节点被替换，删除其右子树的最小元素）。因为假如其被删除，为了B树的平衡稳定，元素数减一，其指针数也要减一。意味着削掉该节点的一棵子树，和树里所有元素，这是不合适的。本文约定：从待删元素的右边相邻子树中，找子树里最小的元素替代之（树里最小元素在树的最左下方。可由平衡树定义得出该结论）。再删掉这个最小元素。该元素位于叶节点里。叶节点里只有元素，没有指针，或者说指针都为空。
??若被删元素位于叶节点，则可以直接删除。因为叶节点没有子树，只有空指针。元素数目可以发生变化，而不影响树里的元素大小排序。若删除元素后该叶节点太小，则可以从其左右相邻兄弟叶节点借一个元素。使其维持在最小节点规模。直至其相邻左右兄弟节点都成为最小节点。若再对该节点删除元素，则合并该节点和其右侧兄弟节点和ta门夹着的父母节点里的对应元素（也可以合并该节点和其左侧兄弟节点，应该都可以。因为这三个节点都是最小节点，但规定合并方向以后，就不能再改变。比如都采用最小节点和右侧兄弟节点合并）。我们称左兄弟为 A，最小节点为 B，右兄弟为C，BC 夹着的父母节点里的元素为 h 合并过程是：把 h 和 C 中的元素都加入 B 里，再删除 H 和 C 。把右兄弟和父母节点里夹着的元素，都插入自身，然后删除右兄弟和父母节点里被这俩子节点夹着的元素。
??若父母节点因为减少一个元素后，比允许最少节点数还少，则按上面的规定方向（和右兄弟），对父母节点这一层节点进行合并。直至根节点。若根节点元素数变为0，则树的高度减一。分支节点合并后变得太大，则需要进行拆分，如同元素插入B 树里的情况。
??非叶节点的元素数如果太少，不允许左右兄弟节点补充元素，只允许合并，调整其在父母节点里的位置。程序里是这么设计的，结果经过大量测试也是正确的。因为所有叶节点必须位于同一层。只能往根节点方向调整。
??下面给一个我画的删除操作流程图：
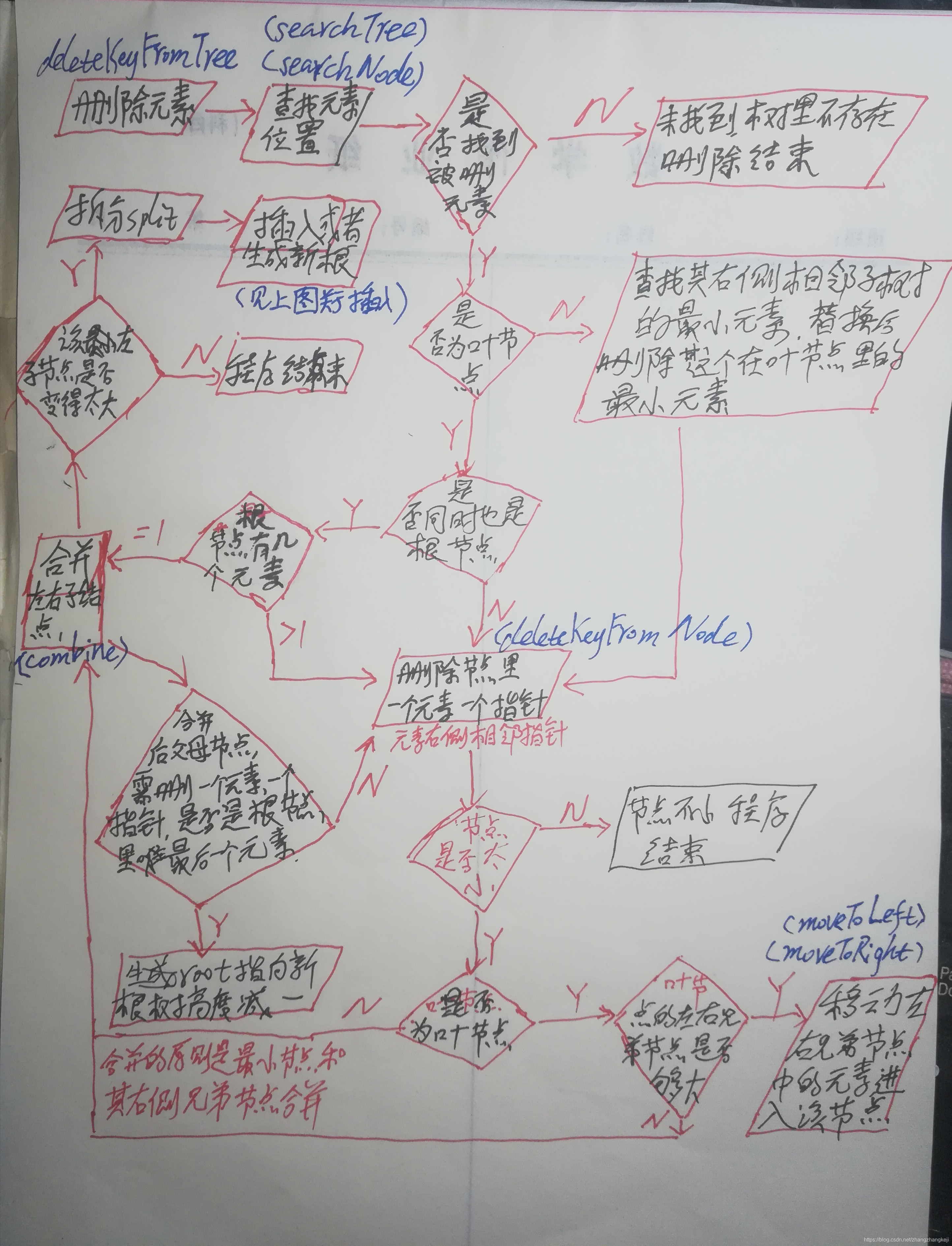
在这里插入图片描述
??图中蓝色标记为对应的函数。
??以下给出各函数说明：
??searchNode ：从具体一个节点里查找待插入元素的位置。
??searchTree ：从树里查找一个元素的位置。
??newRoot ：给树生成一个新的根。比如插入第一个元素的时候，或者新根节点太大，被拆分后。
??split ：分裂太大的节点。节点里的指针和元素，应该同时被分裂。叶节点也不例外。应该注意的是，分裂时，留下了中间那个要插入父母节点的元素。指针则被分成两部分。
??insertNode ：往节点里插入元素，同时也应插入一个指针。
??insertTree ：往树里插入一个元素。其调用了其他函数。
??dispalyCommaExp ：用逗号表达式表示 B 树。格式是先用中括号表示所有元素，在其右侧，用小括号，输出其所有指针指向子树的元素。如 [2,9]( 1, 5, 10 ) 。
??inOrder ：用中序排列给出树里所有元素，程序正确的话，元素应该是递增排列。
??smallNode ：对太小的节点进行处理。或移动其左右兄弟节点中的元素，或合并节点，调用combine函数。
??deleteKeyFromNode ：从节点里删除元素，同时也应删除一个指针。由其他函数保证删除操作前的程序正确性。
??deleteKeyFromTree ：从树里删除一个元素。由其调用其他函数。
??moveToLeft ：从右往左移动元素。右兄弟节点大，可以提供元素。都是叶节点。
??moveToRight ：从左往右移动元素。左兄弟节点大，可以提供元素。都是叶节点。
??combine ：对左右子节点进行合并。对于叶节点，要求都是最小节点。对于分支节点的合并，只要求左子节点是最小节点，右子节点的大小未知。所以可能引起合并后左子节点太大，再重新拆分，产生新的合适的父母节点。
??
??以下是全部代码，先是main函数所在源文件：

#include<iostream>
using namespace std;
#define MAX 7
#define ORDER 5
#define MAXKEYS ORDER - 1
#define MINKEYS (ORDER - 1) / 2

struct Node {
	int numKeys;
	int keyArray[MAX];//关键字和指针均从0开始存储
	Node* ptChildren[MAX];//但关键字数比指针数少一
	Node* ptParent;//由此决定：孩子节点分裂后，往父母节点插入关键字在 i 位置，则，
};				   //新增的指针在父母节点指针数组里，插在 i + 1 位置
// 类似于双向链表，一旦俩节点不再是父母孩子关系，则父母的节点数组还有孩子的父母
//指针，都要进行修改

struct Result {
	Node* pt;
	int index;
	bool findOrNot;
};

extern int searchNode(Node*& pt, int key);
extern Result searchTree(Node * & root,int key);

extern void newRoot(Node*& root, int key, Node* ptLeft, Node* ptRight);
extern void split(Node*& root, Node* ptLeft);
extern void insertNode(Node * &root,Node* pt, int index, int key, Node* ptChild);
extern void insertTree(Node*& root, int key);

extern void dispalyCommaExp(Node * & root);
extern void inOrder(Node*& root);

extern void smallNode(Node * & root,Node* pt);
extern void deleteKeyFromNode(Node*& root, Node* pt, int index);
extern bool deleteKeyFromTree(Node*& root,int key);
extern void moveToLeft(Node* ptParent, int indexKey, Node* ptLeft, Node* ptRight);
extern void moveToRight(Node* ptParent, int indexKey, Node* ptLeft, Node* ptRight);
extern void combine(Node*& root,Node* ptParent, Node* ptLeft, Node* ptRight, int indexKey);

int main() {
	Node* root = NULL;

//	int array[] = { 4, 9, 0, 1, 8, 6, 3, 5, 2, 7 },length = 10;
//	int array[] = { 1, 8, 5, 2, 7 }, length = 5;
//	int array[] = { 4},length = 1 ;
//	int array[] = { 4,0,9,6},length = 4 ;
	int array[] = { 1,2,6,7,11,4,8,13,10,5,17,9,16,20,3,12,14,18,19,15,21,22,23,24,25},length = 25;
//	int array[] = { 1,2,6,7,11,4,8,13,10,5,17,9,16,20,3,12,14,18,19 }, length = 19;
	for (int i = 0; i < length; i++) 
		insertTree(root,array[i]);

	cout << "逗号表达式 ：";
	dispalyCommaExp(root);
	cout <<endl << "中序遍历   ：";
	inOrder(root);
	cout << endl;


	cout << "input number after 'next' to continue test,but 100 means stop test.eg.next:100";
	cout << endl << "input the number you want to delete : ";
	int input;
	do{
		cin >>input ;
		
		cout << endl;
		if (input == 100)
			break;

		if(deleteKeyFromTree(root,input) == false)
			cout << "list does not have this key : "<<input<<'.';
		else {
			dispalyCommaExp(root);
			cout <<endl<< ",中序遍历序列为:";
			inOrder(root);
		}
		cout<< "  next :";
	} while (1 == 1);

	return 0;
}

接着是各函数所在源文件：

#include<iostream>
using namespace std;
#define MAX 7
#define ORDER 5
#define MAXKEYS ORDER - 1
#define MINKEYS (ORDER - 1) / 2

struct Node {
	int numKeys;
	int keyArray[MAX];//关键字和指针均从0开始存储
	Node* ptChildren[MAX];//但关键字数比指针数少一
	Node* ptParent;//由此决定：孩子节点分裂后，往父母节点插入关键字在 i 位置，则，
};				   //新增的指针在父母节点指针数组里，插在 i + 1 位置
// 类似于双向链表，一旦俩节点不再是父母孩子关系，则父母的节点数组还有孩子的父母
//指针，都要进行修改

struct Result {
	Node* pt;
	int index;
	bool findOrNot;
};

int searchNode(Node*& pt, int key) {
	int index;
	for (index = 0; index < pt->numKeys && pt->keyArray[index] < key; index++);
	return index;
}

Result searchTree(Node*& root, int key) {
	Result result;
	Node* pt = root, * ptParent = NULL;
	int index = 0;

	while (pt != NULL) {
		index = searchNode(pt, key);

		if (index == pt->numKeys || pt->keyArray[index] != key) {
			ptParent = pt;
			pt = pt->ptChildren[index];
		}
		else
			break;
	}

	result.index = index;
	if (pt != NULL) {
		result.findOrNot = true;
		result.pt = pt;
	}
	else {
		result.findOrNot = false;
		result.pt = ptParent;
	}

	return result;
}

void newRoot(Node*& root, int key, Node* ptLeft, Node* ptRight) {
	root = new Node;

	root->numKeys = 1;
	root->ptParent = NULL;
	root->keyArray[0] = key;

	root->ptChildren[0] = ptLeft;
	if (ptLeft != NULL)
		ptLeft->ptParent = root;

	root->ptChildren[1] = ptRight;
	if (ptRight != NULL)
		ptRight->ptParent = root;
}

void split(Node*& root, Node* ptLeft) {
	void insertNode(Node * &root, Node * pt, int index, int key, Node * ptChild);
	Node * ptRight = new Node;

	ptRight->numKeys = MINKEYS;
	ptLeft->numKeys = MAXKEYS - MINKEYS;

	ptRight->ptParent = ptLeft->ptParent;

	for (int i = 0, j = ptLeft->numKeys; i < MINKEYS; i++) {
		ptRight->keyArray[i] = ptLeft->keyArray[j + 1 + i];

		ptRight->ptChildren[i] = ptLeft->ptChildren[j + 1 + i];
		if (ptRight->ptChildren[i] != NULL)
			ptRight->ptChildren[i]->ptParent = ptRight;
	}
	ptRight->ptChildren[MINKEYS] = ptLeft->ptChildren[ORDER];
	if (ptRight->ptChildren[MINKEYS] != NULL)
		ptRight->ptChildren[MINKEYS]->ptParent = ptRight;

	if (ptLeft == root)  //根节点被拆分,生成新根
		newRoot(root, ptLeft->keyArray[ptLeft->numKeys], ptLeft, ptRight);
	else
		insertNode(root, ptLeft->ptParent, 
			searchNode(ptLeft->ptParent, ptLeft->keyArray[ptLeft->numKeys]),
			ptLeft->keyArray[ptLeft->numKeys], ptRight);
}

void insertNode(Node*& root, Node* pt, int index, int key, Node* ptChild) {
	if (root == NULL) {
		newRoot(root, key, NULL, NULL);
		return;
	}

	int i;
	for (i = pt->numKeys;i > index; i--) {
		pt->keyArray[i] = pt->keyArray[i - 1];
		pt->ptChildren[i + 1] = pt->ptChildren[i];
	}

	pt->keyArray[index] = key;
	pt->numKeys++;

	pt->ptChildren[index + 1] = ptChild;

	if (pt->numKeys == ORDER)
		split(root,pt);
}

void insertTree(Node*& root, int key) {
	Result result = searchTree(root, key);

	if (result.findOrNot == false)
		insertNode(root,result.pt,result.index,key,NULL);
}

void dispalyCommaExp(Node*& root) {
	if (root == NULL)
		return;

	int i;
	if (root->ptChildren[0] == NULL) {
		cout << '[';

		for (i = 0; i < root->numKeys - 1; i++)
			cout << root->keyArray[i] << ' ';

		cout << root->keyArray[i];
		cout << ']';
		return;
	}

	cout << '[';

	for (i = 0; i < root->numKeys - 1; i++)
		cout << root->keyArray[i] << ' ';

	cout << root->keyArray[i];
	cout << "](";

	for (i = 0; i < root->numKeys; i++) {
		dispalyCommaExp(root->ptChildren[i]);
		cout << ',';
	}
	dispalyCommaExp(root->ptChildren[i]);
	cout << ')';
}

void inOrder(Node*& root) {
	if (root == NULL)
		return;

	if (root->ptChildren[0] == NULL) {
		for (int i = 0; i < root->numKeys; i++)
			cout << root->keyArray[i] << ' ';
		return;
	}

	for (int i = 0; i < root->numKeys; i++) {
		inOrder(root->ptChildren[i]);
		cout << root->keyArray[i] << ' ';
	}
	inOrder(root->ptChildren[root->numKeys]);
}

void moveToLeft(Node* ptParent, int indexKey, Node* ptLeft, Node* ptRight) {
	ptLeft->keyArray[ptLeft->numKeys] = ptParent->keyArray[indexKey];
	ptLeft->numKeys++;

	ptParent->keyArray[indexKey] = ptRight->keyArray[0];

	for (int i = 0; i < ptRight->numKeys - 1; i++)
		ptRight->keyArray[i] = ptRight->keyArray[i + 1];
	ptRight->numKeys--;
}

void moveToRight(Node* ptParent, int indexKey, Node* ptLeft, Node* ptRight) {
	for (int i = ptRight->numKeys; i > 0; i--)
		ptRight->keyArray[i] = ptRight->keyArray[i - 1];
	ptRight->keyArray[0] = ptParent->keyArray[indexKey];
	ptRight->numKeys++;

	ptParent->keyArray[indexKey] = ptLeft->keyArray[ptLeft->numKeys - 1];
	ptLeft->numKeys--;
}

void combine(Node*& root,Node* ptParent, Node* ptLeft, Node* ptRight, int indexKey) {
	void deleteKeyFromNode(Node * &root, Node * pt, int index);
	
	if (ptParent->numKeys > 0) {
		ptLeft->keyArray[ptLeft->numKeys] = ptParent->keyArray[indexKey];

		ptLeft->numKeys++;
	}

	if (ptLeft != NULL) {  //左右指针一个不为空，同层都不为空
		for (int i = 0; i < ptRight->numKeys; i++)
			ptLeft->keyArray[ptLeft->numKeys + i] = ptRight->keyArray[i];

		ptLeft->numKeys = ptLeft->numKeys + ptRight->numKeys;


		if (ptRight->ptChildren[0] != NULL)
			for (int i = 0, j = ptLeft->numKeys - ptRight->numKeys; i <= ptRight->numKeys; i++) {
				ptLeft->ptChildren[j + i] = ptRight->ptChildren[i];
				ptRight->ptChildren[i]->ptParent = ptLeft;
			}
	}

	delete ptRight;	//ptRight已经没有用了

	if (ptParent == root && indexKey == 0 && root->numKeys == 1) //三条件缺一不可
		root->numKeys = 0;
	deleteKeyFromNode(root,ptParent,indexKey);

	if (ptLeft!= NULL && ptLeft->numKeys > MAXKEYS)
		split(root,ptLeft);
}

void smallNode(Node * & root,Node* pt) {
	Node* ptParent = pt->ptParent;
	int indexPt;
	for (indexPt = 0; ptParent->ptChildren[indexPt] != pt; indexPt++);

	if (indexPt == 0)
		if (pt->ptChildren[0] == NULL && ptParent->ptChildren[1]->numKeys > MINKEYS)
			moveToLeft(ptParent, 0, pt, ptParent->ptChildren[1]);
		else
			combine(root,ptParent, pt, ptParent->ptChildren[1], 0);
	else if (indexPt == ptParent->numKeys)
		if (pt->ptChildren[0] == NULL && ptParent->ptChildren[indexPt - 1]->numKeys > MINKEYS)
			moveToRight(ptParent, ptParent->numKeys - 1, ptParent->ptChildren[indexPt - 1], pt);
		else
			combine(root,ptParent, ptParent->ptChildren[indexPt - 1], pt, indexPt - 1);
	else if (pt->ptChildren[0] == NULL && ptParent->ptChildren[indexPt - 1]->numKeys > MINKEYS)
		moveToRight(ptParent, indexPt - 1, ptParent->ptChildren[indexPt - 1], pt);
	else if (pt->ptChildren[0] == NULL && ptParent->ptChildren[indexPt + 1]->numKeys > MINKEYS)
		moveToLeft(ptParent, indexPt, pt, ptParent->ptChildren[indexPt + 1]);
	else
		combine(root,ptParent, pt, ptParent->ptChildren[indexPt + 1], indexPt);
}

void deleteKeyFromNode(Node*& root, Node* pt, int index) {
	if(pt == root)
		if (root->numKeys == 0) {     //对应被函数 combine 调用。直接降低高度，
			Node* ptDelete = root;	  //不再重复执行合并

			root = root->ptChildren[0];
			if (root != NULL)
				root->ptParent = NULL;
			delete ptDelete;
			ptDelete = NULL;
			return;
		}
		else if(root->numKeys == 1){  //对应被deleteKeyFromTree调用，删除根节点里
			root->numKeys = 0;		//最后一个元素，需要调用combine合并节点
			combine(root,root,root->ptChildren[0],root->ptChildren[1],-1);
			return;
		}

	for (int j = index; j < pt->numKeys - 1; j++) {
		pt->keyArray[j] = pt->keyArray[j + 1];
		pt->ptChildren[j + 1] = pt->ptChildren[j + 2];
	}
	pt->numKeys--;

	if (pt != root && pt->numKeys < MINKEYS)
		smallNode(root,pt);
}

bool deleteKeyFromTree(Node*& root, int key) {
	Result result = searchTree(root, key);

	if (result.findOrNot == false)
		return false;

	if (result.pt->ptChildren[0] == NULL)  //调用删除操作，务必保留根节点不变
		deleteKeyFromNode(root,result.pt, result.index);
	else {
		Node* ptMin = result.pt->ptChildren[result.index + 1];
		while (ptMin->ptChildren[0] != NULL)
			ptMin = ptMin->ptChildren[0];

		result.pt->keyArray[result.index] = ptMin->keyArray[0];

		deleteKeyFromNode(root,ptMin, 0);
	}

	return true;
}

测试结果和对应图如下：
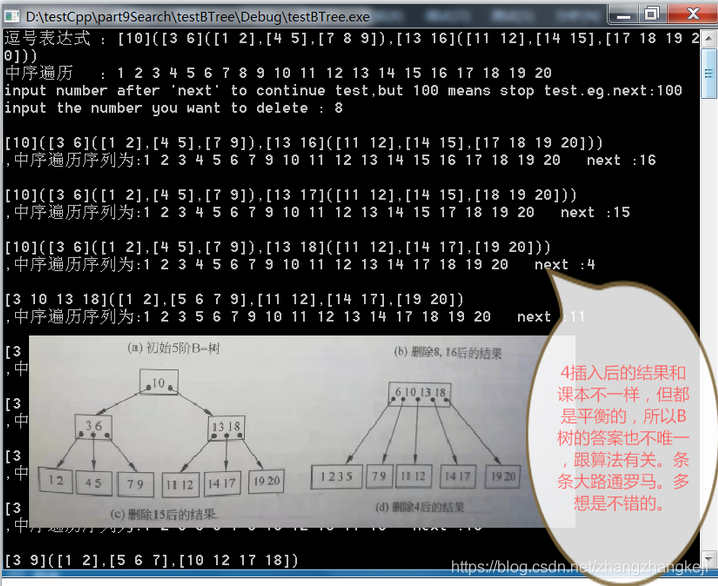
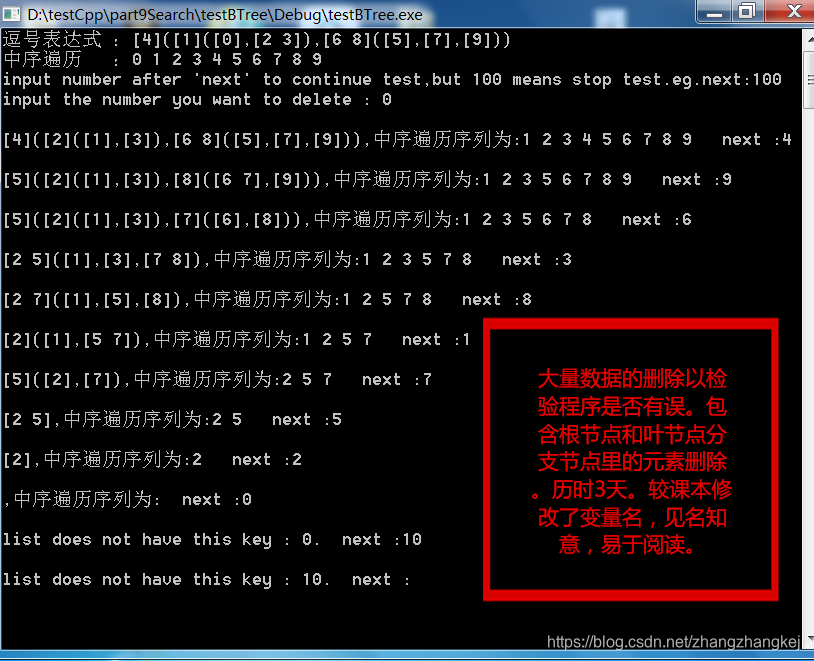
在这里插入图片描述

测试含有25个元素的大 B 树。测试程序的综合性能。除了根节点用引用 & ，其余的指针值传递。要不程序互相调用后，指针读写会出错，比如引用了一个函数里定义的变量，而该函数已经结束，所有变量被销毁，对其中动态局部变量的引用就不合适了。。
谢谢阅读。有懒猫老师的视频，就不这么费力了。