相关知识:Dijkstra算法(建议重点掌握堆优化算法)/Floyd算法/SPFA(严重不推荐)
由于SPFA算法时效性无法保证,理应为历史淘汰的算法,本文不讲述。
一、Dijkstra算法
1.1 普通算法
该算法由著名计算机科学家Edsger Wybe Dijkstra提出,使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题。该算法至今在各类地图等商业环境被广泛使用,是知名度非常高的算法之一。该算法的核心是贪心策略,以下图例子为展开
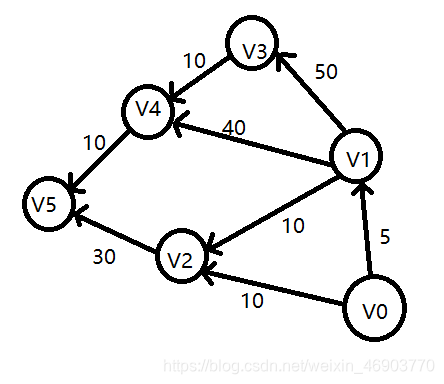
本例中以V0为原点。首先声明一个数组dis,保存从原点到各点的最短距离,这时V0离V0到V5距离分别为0,5,10,∞,∞,∞。
再声明一个集合T,用以储存已经找到原点到各个顶点最短路径的集合,此时需要注意的是,虽然我们能看出V0到V1和V2距离是已知的,但是并没有经过计算,所以T中不能储存V1和V2。此时的T={V1}。
既然是从V0开始,我们就从V0出发寻找下一个顶点,图中可知离V0最近的是V1,此时V0到V1的距离就是经过计算的确定的值,也就是5。
确定V1之后,V0到V2也可以确定,如果从V0直接到V2距离是10,如果V0通过V1到V2距离为5+10=15,所以V0到V2距离为确定的值=5。
以此类推,V0到V3距离为55,到V4距离为45,到V5距离为40。
1.2 堆优化算法
由于在竞赛中使用Dijkstra算法的普通算法(即上文讲述)经常会导致超时等问题,这里推荐一种Dijkstra算法的堆优化方法。
Dijkstra普通算法的实现需要从头到尾扫一遍点找出最小的点然后进行松弛。这个扫描操作就是坑害Dijkstra普通算法时间复杂度的罪魁祸首。所以我们使用小根堆,用优先队列来维护这个“最小的点”。从而大大减少Dijkstra算法的时间复杂度。
首先,我们需要往优先队列中push最短路长度,但是它一旦入队,就会被优先队列自动维护离开原来的位置,换言之,我们无法再把它与它原来的点对应上,也就是说没有办法形成点的编号到点权的映射。
我们用pair解决这个问题。
pair是C++自带的二元组。我们可以把它理解成一个有两个元素的结构体。更刺激的是,这个二元组有自带的排序方式:以第一关键字为关键字,再以第二关键字为关键字进行排序。所以,我们用二元组的first位存距离,second位存编号即可。
然后我们发现裸的优先队列其实是大根堆,我们如何让它变成小根堆呢?
有两种方法,第一种是把第一关键字取相反数,取出来的时候再取相反数。
二、Floyd算法
弗洛伊德算法是由计算机科学家罗伯特·弗洛伊德提出的。是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题,同时也被用于计算有向图的传递闭包。

该算法首先列出从每一点出发找到可以直接通往其他顶点的初始化矩阵,我们以上图为例得到矩阵D:
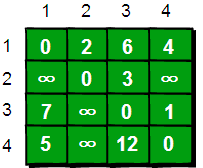
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4到3的路程d[4][3]原本是12。如果只通过1中转(4->1->3),路程将缩短为11(d[4][1]+d[1][3]=5+6=11)。其实1号到3号也可以通过2中转,使得1到3的路程缩短为5(d[1][2]+d[2][3]=2+3=5)。所以如果同时经过1和2中转的话,从4到3的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。
假如现在只允许经过1号顶点,求任意两点之间的最短路程,只需判断d[i][1]+d[1][j]是否比d[i][j]要小即可。d[i][j]表示的是从i号顶点到j号顶点之间的路程。d[i][1]+d[1][j]表示的是从i号顶点先到1号顶点,再从1号顶点到j号顶点的路程之和。其中i是1-n循环,j也是1-n循环。
通过以上方法,加入一部分暴力求解方法,即可求出第十二届蓝桥杯第一轮省赛C/C++的E题:

参考文献(本文参考或引用下列部分文献)
[1] 严蔚敏.李冬梅.吴伟民. 数据结构(C语言版)[M]. 第二版. 北京:人民邮电出版社, 2015 :170-176.
[2] 陈锋. 算法竞赛入门经典[M]. 1. 北京:清华大学出版社, 2021 :374-394.
[3] Ouyang_Lianjun. 最短路径问题—SPFA算法详解[EB/OL]. 2017[2021-8-22]. https://blog.csdn.net/qq_35644234/article/details/61614581.
[4] Ouyang_Lianjun. 最短路径问题—Dijkstra算法详解[EB/OL]. 2017[2021-8-22]. https://blog.csdn.net/qq_35644234/article/details/60870719.
[5] dogs~xiaofei. 第十二届蓝桥杯B组题目及题解[EB/OL]. 2021[2021-8-22]. https://blog.csdn.net/weixin_49444351/article/details/116395998.
[6] JDFZ 2019级 蒟蒻OIer. Dijkstra算法堆优化详解[EB/OL]. [2021-8-23]. https://www.cnblogs.com/fusiwei/p/11390537.html.