[C++知识库]PTA甲级 1125 Chain the Ropes (C++)

Given some segments of rope, you are supposed to chain them into one rope. Each time you may only fold two segments into loops and chain them into one piece, as shown by the figure. The resulting chain will be treated as another segment of rope and can be folded again. After each chaining, the lengths of the original two segments will be halved.

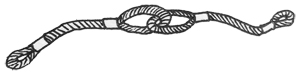
Your job is to make the longest possible rope out of $N$ given segments.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer $N(2\le N\le 10^4)$. Then $N$ positive integer lengths of the segments are given in the next line, separated by spaces. All the integers are no more than $10^4$.

Output Specification:

For each case, print in a line the length of the longest possible rope that can be made by the given segments. The result must be rounded to the nearest integer that is no greater than the maximum length.

Sample Input:

8
10 15 12 3 4 13 1 15

Sample Output:

14

Caution:

比较有意思的一道小题目，其实想通了之后代码很简单，首先两段绳子，合成一次后变成一段，绳子段数减一，所以n段绳子要想最终变成 1 段绳子，一定要合成n-1次，而每段最初的绳子每被用来合成一次，他在最终绳子中的贡献就少一半，所以我们要尽量不浪费最初的资源，就要每次都让最短的两根绳子来合成（这样的话最长的绳子一定是在最后被用来合成，他在最终的绳子中的贡献就最大）。

代码就是先排序，然后i从1到n-1遍历数组，每次更新nums[i]为(nums[i] + nums[i - 1]) / 2，表示用这两根绳子来合成新绳子（为什么合成新绳子后不用再排序呢？因为新合成的绳子的长度是原来两根绳子的一半，所以新的nums[i]一定小于旧的nums[i]，自然一定小于nums[i + 1]。

Solution:

// Talk is cheap, show me the code
// Created by Misdirection 2021-08-27 22:20:44
// All rights reserved.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main(){
    int n;
    scanf("%d", &n);

    vector<double> nums(n);

    for(int i = 0; i < n; ++i) cin >> nums[i];
    sort(nums.begin(), nums.end());

    for(int i = 1; i < n; ++i) nums[i] = (nums[i] + nums[i - 1]) / 2;

    printf("%d\n", (int)nums[n - 1]);
    
    return 0;
}