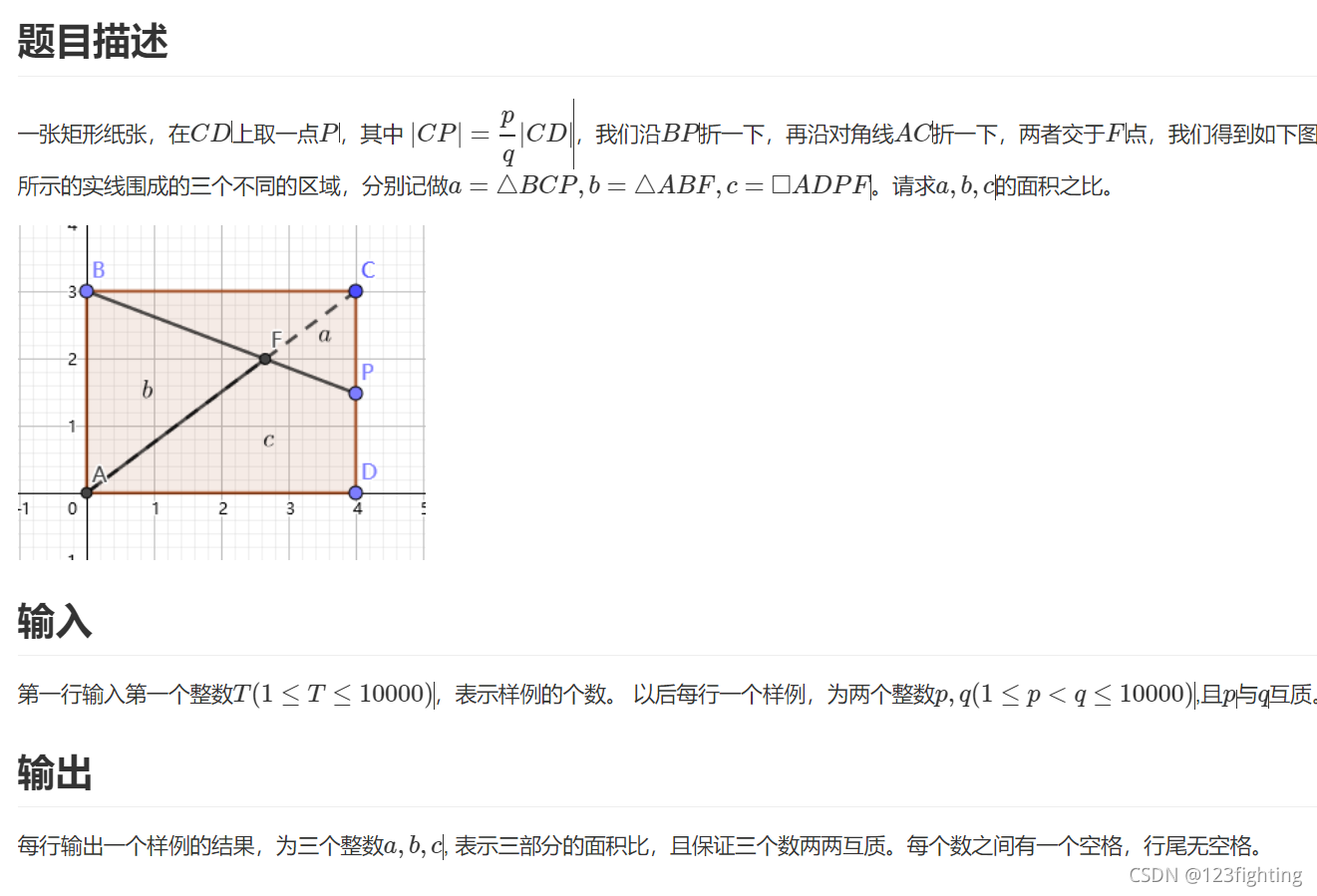
要点:
这种题主要就是找规律,得到计算表达式。
AC:y=3/4x BP:y=-|CP|/4x+3
找出AC与BP两条直线相交F的坐标为(12/(3+|CP|),3/4x)
a
=
△
B
C
P
=
2
∣
C
P
∣
=
2
×
p
q
×
3
=
6
p
q
=
6
p
(
p
+
q
)
(
p
+
q
)
q
a=\bigtriangleup BCP=2|CP|=2\times\frac{p}{q}\times3=\frac{6p}{q}=\frac{6p\left( p+q \right)}{\left( p+q \right) q}
a=△BCP=2∣CP∣=2×qp?×3=q6p?=(p+q)q6p(p+q)?
b
=
△
A
B
F
=
3
2
×
(
12
3
+
∣
C
P
∣
)
=
18
3
+
∣
C
P
∣
=
=
6
q
p
+
q
=
6
q
2
p
+
q
b=\bigtriangleup ABF=\frac{3}{2}\times \left( \frac{12}{3+|CP|} \right) =\frac{18}{3+|CP|}==\frac{6q}{p+q}=\frac{6q^2}{p+q}
b=△ABF=23?×(3+∣CP∣12?)=3+∣CP∣18?==p+q6q?=p+q6q2?
c
=
梯形
P
D
A
B
?
b
=
12
q
?
6
p
q
?
6
q
p
+
q
=
6
(
q
2
?
p
2
+
p
q
)
(
p
+
q
)
q
c=\text{梯形}PDAB-b=\frac{12q-6p}{q}-\frac{6q}{p+q}=\frac{6\left( q^2-p^2+pq \right)}{\left( p+q \right) q}
c=梯形PDAB?b=q12q?6p??p+q6q?=(p+q)q6(q2?p2+pq)?
代码
#include <stdio.h>
int gcd(int x,int y);
int main()
{
int T,p,q,a,b,c,gys;
scanf("%d",&T);
while(T--){
scanf("%d%d",&p,&q);
a=p*p+p*q;
b=q*q;
c=q*q-p*p+p*q;
gys=gcd(a,b);
gys=gcd(gys,c);
printf("%d %d %d\n",a/gys,b/gys,c/gys);
}
}
int gcd(int x,int y)
{
if(y==0) return x;
else return gcd(y,x%y);
}