[C++知识库]C语言求排列组合和阶乘

关于C语言求排列数、组合数以及阶乘的实验记录：

一、求排列数和组合数

以下公式中A(n,m)为排列数公式，C(n,m)为组合数公式。

$$\begin{array}{rlr}& C_n^m=\frac{n!}{m!(n?m)!}=\frac{A_n^m}{m!}=C_{n?1}^m+C_{n?1}^{m?1}& \\ & & \\ & A_n^m=n(n?1)(n?2)...(n?m+1)=\frac{n!}{(n?m)!}& \\ & & \\ & A_n^m=n?A_{n?1}^{m?1}=(n?m+1)?A_n^{m?1}& \end{array}$$

代码实现：

1.通过阶乘求解：

#include <stdio.h>
double fact(int s) //求阶乘函数，返回s的阶乘
{
	if (s == 0 || s == 1)
		return 1;
	else
		return s * fact(s - 1);
}
double C(int n, int m) //通过调用求阶乘函数fact求解组合数A(n,m)的值
{
	return fact(n) / fact(m) / fact(n - m);
}
double A(int n, int m) //通过调用求阶乘函数fact求解排列数A(n,m)的值
{
	return fact(n) / fact(n - m);
}
int main(void)
{
	int n = 0, m = 0;
	while (1)
	{
		printf("输入自然数n,m（保证n>=m）：");
		scanf("%d%d", &n, &m);
		if (n < m || n < 0 || m < 0)
			printf("输入有误，重新输入！\n\n");
		else
		{
			printf("排列：A(%d,%d) = %.0lf\n", n, m, A(n, m));
			printf("组合：C(%d,%d) = %.0lf\n\n", n, m, C(n, m));
		}
	}
	return 0;
}

2.通过递归求解：

#include <stdio.h>
double C(int n, int m) //通过递归求解组合C(n,m)的值
{
	if (m == 0 || m == n)
		return 1;
	else
		return C(n - 1, m) + C(n - 1, m - 1);
}
double A(int n, int m) //通过递归求解排列A(n,m)的值
{
	if (m == 0)
		return 1;
	else if (m == 1)
		return n;
	else
		return n * A(n - 1, m - 1); //也可以换成： (n - m + 1) * A(n, m - 1);
}
int main(void)
{
	int n = 0, m = 0;
	while (1)
	{
		printf("输入自然数n,m（保证n>=m）：");
		scanf("%d%d", &n, &m);
		if (n < m || n < 0 || m < 0)
			printf("输入有误，重新输入！\n\n");
		else
		{
			printf("排列：A(%d,%d) = %.0lf\n", n, m, A(n, m));
			printf("组合：C(%d,%d) = %.0lf\n\n", n, m, C(n, m));
		}
	}
	return 0;
}

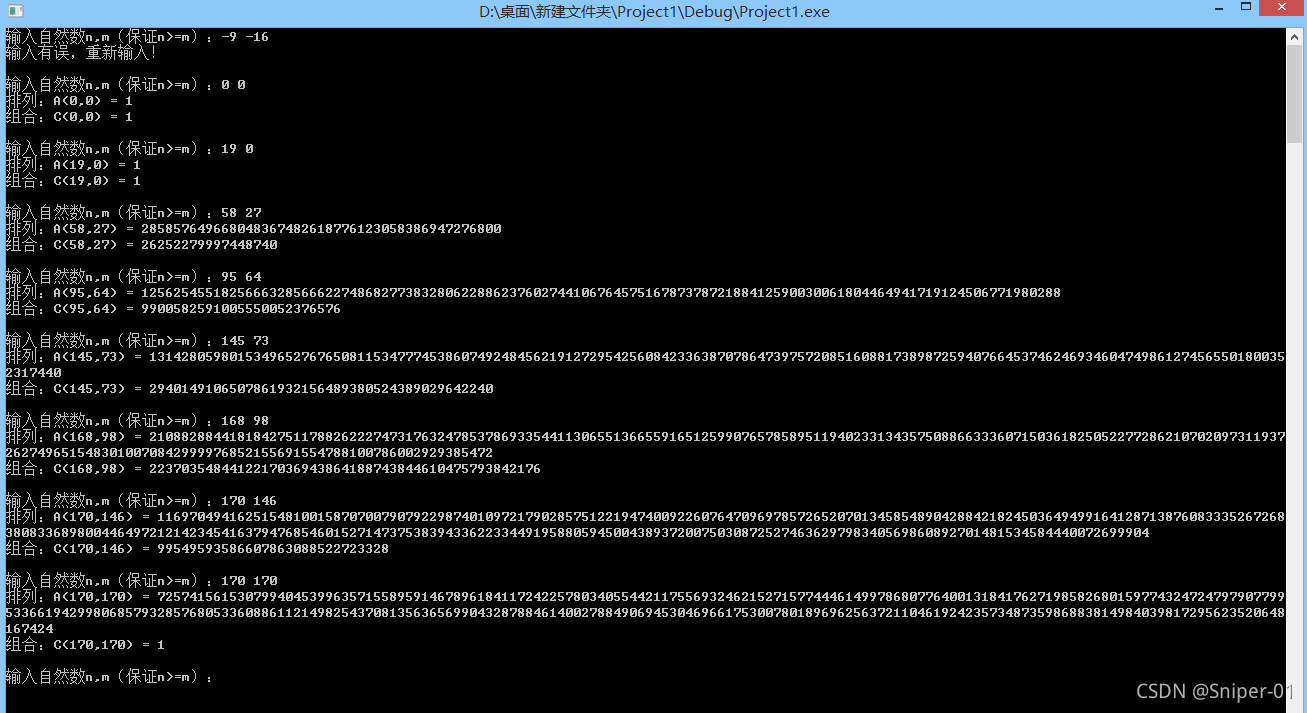
运行结果：

总结：

以上两种求解方式推荐第一种，运算速度比第二种快很多。

二、求阶乘

上述求排列数和组合数所推荐的第一种方式其核心在于求阶乘，下面给出两种求阶乘的方式。

1.通过循环求阶乘：

double fact(int s) //求阶乘函数，返回s的阶乘
{
	double fa = 1;
	while (s--)  fa *= (s + 1);
	return fa;
}

2.通过递归求阶乘：

double fact(int s) //求阶乘函数，返回s的阶乘
{
	if (s == 0 || s == 1)
		return 1;
	else
		return s * fact(s - 1);
}

两种方式对比：

#include <stdio.h>
double fact1(int s) //通过循环求阶乘函数，返回s的阶乘
{
	double fa = 1;
	while (s--)  fa *= (s + 1);
	return fa;
}
double fact2(int s) //通过递归求阶乘函数，返回s的阶乘
{
	if (s == 0 || s == 1)
		return 1;
	else
		return s * fact2(s - 1);
}
int main(void)
{
	int n = 0;
	while (1)
	{
		printf("输入一个自然数：");
		scanf("%d", &n);
		printf("通过循环求出其阶乘为：\n%.0lf\n\n", fact1(n));
		printf("通过递归求出其阶乘为：\n%.0lf\n\n", fact2(n));
	}
	return 0;
}

运行结果：

总结：

从25的阶乘开始，两种方式所计算出的阶乘结果便开始出现精度不足的情况，这是因为double类型数据的精度为15~16位。从图中也可以看到，结果是从 25! 的第17位开始出现差距的，此外，本次实验最多只能计算到170的阶乘，超过之后，便无法通过本程序求得，这是因为double所能表示的数据范围为：-2¹⁰²⁴ ~ +2¹⁰²⁴ ，也即-1.79E+308 ~ +1.79E+308。而170的阶乘约为：7.26E+306左右，171的阶乘约为：1.24E+309左右，这已经超出了double类型所能表示的最大值，所以无法求得。