[C++知识库]ComSec学前作业一：C语言程序包GMP的使用

GMP库的应用:
参考网站:
https://blog.csdn.net/m0_43406494/article/details/109089658
https://blog.csdn.net/m0_46296905/article/details/117091377
https://blog.csdn.net/qq_40129237/article/details/81286199

GMP版本：6.2.1
平台:WSL2上的Ubuntu18.04LTS

代码:

#include <gmp.h>
#include <iostream> 
using namespace std;
	
void Euler(mpz_t p, mpz_t q,mpz_t euler)
{
	mpz_t one,i,j;
	mpz_init(i);
	mpz_init(j);
	//防止p，q值被修改
	 
	mpz_init_set_str(one,"1",10);
	mpz_sub(i,p,one);
	mpz_sub(j,q,one);
	mpz_mul(euler,i,j);
	
	mpz_clear(i); 
	mpz_clear(j); 
	mpz_clear(one); 
}
//欧拉函数性质：m和n互素，则m，n的乘积的欧拉值，等于m的欧拉值和n的欧拉值的乘积， 
//素数的欧拉值等于自身减一
//所以n = pq的欧拉值等于(p-1)(q-1) 

int main(){
	gmp_randstate_t grt;
	gmp_randinit_default(grt); 
	gmp_randseed_ui(grt, time(NULL)); 
	
	mpz_t p,q;
	mpz_init(p); 
	mpz_init(q);
 
	mpz_urandomb(p, grt, 512);
	mpz_urandomb(q, grt, 512);
 
	mpz_nextprime(p, p); 
	mpz_nextprime(q, q);
//生成p,q大素数	
 
	mpz_t n;
	mpz_init(n);
	mpz_mul(n, p, q); 
//求p，q的乘积	
	
	mpz_t euler;
	mpz_init(euler); 
	Euler(p,q,euler);
//求欧拉值	
	
	gmp_printf("p = %ZX\n\n", p);
	gmp_printf("q = %ZX\n\n", q);
	gmp_printf("n = %ZX\n\n", n);
	gmp_printf("euler = %ZX\n\n",euler);
	//十六进制输出
	
	mpz_clear(q);
	mpz_clear(p);
	mpz_clear(n);
	mpz_clear(euler);

	return 0;

}

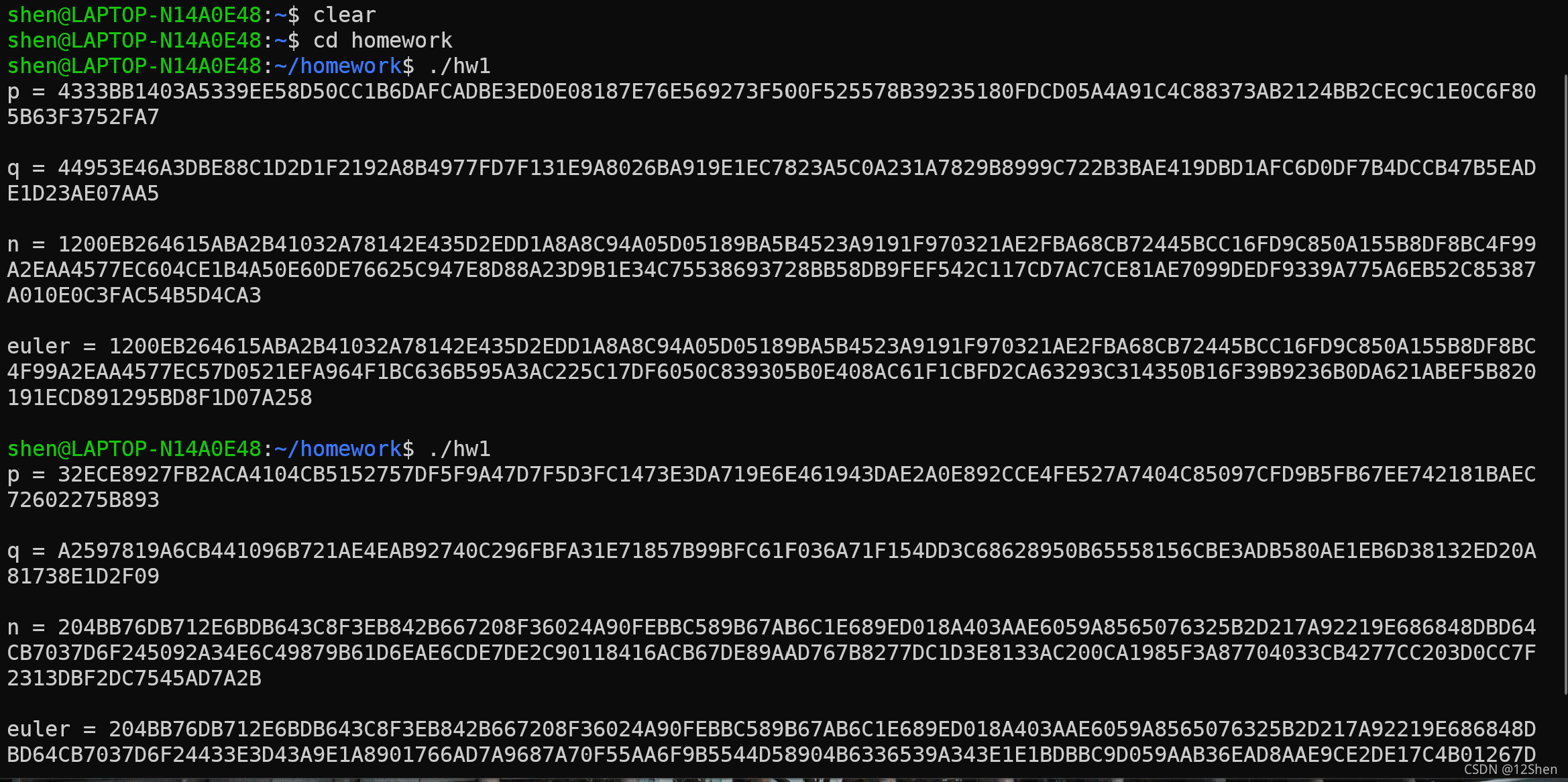
运行结果: