[C++知识库]C++二分遍历

代码存档

#include<iostream>
using namespace std;
//数组查找的二分遍历法
//传入参数：数组本身arr，数组内寻找的元素K，数组长度n
int binary(int* arr, int K, int n) {
	//头下标与尾下标
	int front = -1;
	int rear = n;
	//当数组不是空的时候进行二分遍历
	while (front + 1 != rear) {
		//找到数组中间下标（中间大）
		int i = (front + rear) / 2;
		
		if (K < arr[i]) {
			rear = i;
		}
		if (K>arr[i])
		{
			front = i;
		}
		if(K==arr[i])
		{
			return i;
		}
	}
}
int main() {
	int array[16] = { 11,13,21,26,29,36,40,41,45,51,54,56,65,72,77,83 };
	int n = sizeof(array) / sizeof(array[0]);
	cout << binary(array, 45, n) << endl;
	system("pause");
	return 0;
}

原理分析：

二分遍历与顺序遍历的方法明显不同。顺序遍历的时间代价比较大，代码为：

int Sequential(int* arr, int K, int n) {
	for (int i = 0; i < n; i++)
	{
		if (K==arr[i])
		{
			return i;
		}
	}
}

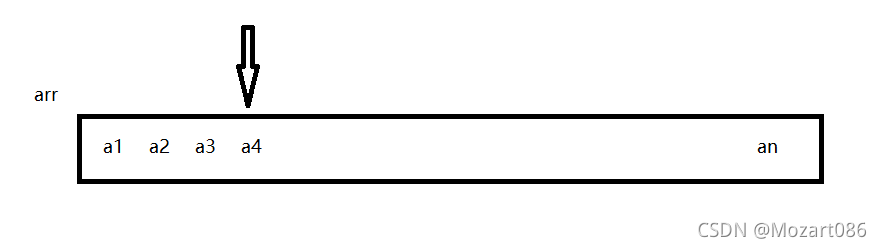
顺序遍历，逐一比对，返回元素下标。但是i需要每一个元素都进行遍历。

二分遍历原理分析

1. 存储数组

2. 设置浮标front与rear用于存放首元素下标与尾部元素下标

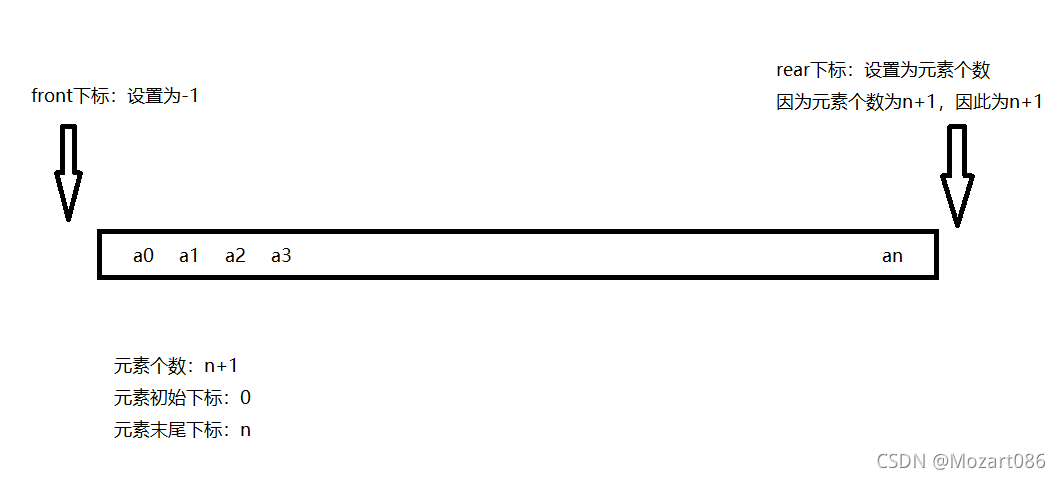
3. 判断循环条件：头部下标和尾部下标不相邻

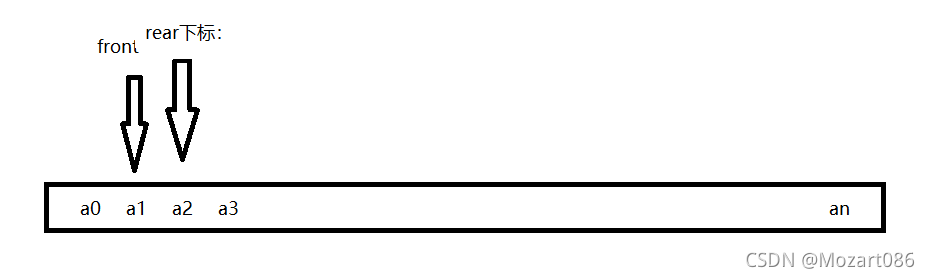
此时没有遍历的必要。

4. 二分遍历：

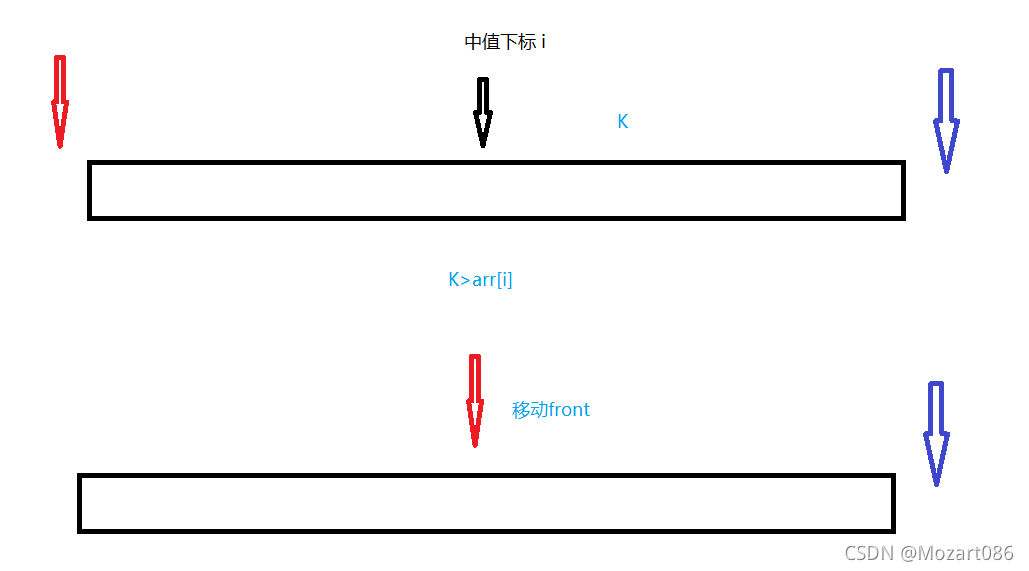
（1）找到中间值下标：

int i = (front + rear) / 2;

注意是整型，奇数除以2取小值

（2）比对，当值大于中值时，头下标等于中值下标；当值小于中值时，尾部下标等于中值下标；当值等于中值时，返回中值下标。以此类推。

?

一次循环可以左右遍历，直到找到合适的值的下标。