对顶栈
基本概念:用两个栈实现。一个栈记录数列光标前的数,另一个栈记录光标后的数,栈顶都是光标方向。
实际作用:可以解决有光标,且一次操作只能移动一位,添加,删除等都是点操作且位置一定在光标左右的问题。
效率:由于每个元素只需要进出栈一次,所以时间复杂度是O(n)
接下来来看一道十分经典的题

输入:
8
I 2
I -1
I 1
Q 3
L
D
R
Q 2
输出:
2
3
分析题目:
由于这道题需要求序列中前i个数(从第1个数开始求和)的最大值,那么我们可以定义一个数组sum[ ]用来记录数组的前缀和,用d[ ]数组来记录前i个数求和的最大值。想到了这里,那么我们只需要用对顶栈存序列,并且让光标一直在两个栈顶移动,便能找到答案。那么如何维护这个对顶栈呢?显然对于插入操作,我们只需要将元素全部入栈1,并且更新前缀和和最大值两个数组即可;对于光标左移操作,因为光标左移后,光标右边的元素还存在,没有被删掉,我们可以把这部分元素压入栈2,并且在栈1中弹出,这样栈1的栈顶依旧是光标位置;然后对于删除操作:我们只需要删除栈1的栈顶元素,那么光标自然就指向了被删元素左边第一个元素(当然得判断栈非空);最后也是最重要的光标右移操作:光标右移我们只需要再将栈2的栈顶元素压入栈1当中,然后栈2弹出即可,但是由于光标右移操作可能是在删除操作之后,那么此时的前缀和和最大值数组就会有变动,所以需要重新更新数组。到此,思路就已经很清晰了,相信读者也能做出这道经典题了。
AC代码如下
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
const int maxn=1e6+7;
int n,x,sum[maxn],d[maxn];
char c;
int main(){
iostream::sync_with_stdio(false);
while(cin>>n){
int cnt=0;
memset(sum,0,sizeof(sum));
memset(d,-INF,sizeof(d));
stack<int>s1,s2;
for(int i=1;i<=n;i++){
cin>>c;
if(c!='I'&&c!='Q'){
if(c=='L'&&!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
else if(c=='R'&&!s2.empty()){
s1.push(s2.top());
sum[s1.size()]=sum[s1.size()-1]+s2.top();
d[s1.size()]=max(d[s1.size()-1],sum[s1.size()]);
s2.pop();
}
else if(c=='D'&&!s1.empty()) s1.pop();
}
else{
cin>>x;
if(c=='I') {
s1.push(x);
sum[s1.size()]=sum[s1.size()-1]+s1.top();
d[s1.size()]=max(d[s1.size()-1],sum[s1.size()]);
}
else if(c=='Q') cout<<d[x]<<endl;
}
}
}
return 0;
}
单调栈
基本概念:从栈顶到栈底保持一个单调递增或者单调递减的顺序的栈。(本质上还是一个栈)
实际作用:用于找到序列中某一个元素左边第一个比它大(或者小 的元素的位置和 右边第一个比他它小(或者大) 的元素的位置。
效率:由于序列中每个元素最多进出栈一次,所以时间复杂度是O(n).
大致图形: 以序列 1 4 5 2 7为例

那么我们应该如何维护单调栈呢?竟然已经知道了它的内部逻辑,我们不妨按照以下的步骤去维护这个栈。(假设以单调递增栈为例),对于一个无序序列,我们从头开始遍历。如果栈为空或者当前元素小于栈顶元素,那么就让这个元素入栈;否则,就让栈顶元素出栈,并且比较此时栈顶元素和当前元素的大小,一直到栈为空或者栈顶元素大于当前元素时,将当前元素入栈。
模板代码:
stack<int>s;
for(int i=1;i<=n;i++){
if(s.empty()||a[i]<s.top()) s.push(a[i]);
else{
while(!s.empty()&&a[i]>=s.top()) s.pop();
s.push(a[i]);
}
}
接下来,我们来看一道简单的模板题
(洛谷)P5788 【模板】单调栈
给出项数为 n的整数数列a1…n。
定义函数 f(i) 代表数列中第 i 个元素之后第一个大于ai的元素的下标,即f(i)=min i<j≤n,aj>ai?{j}。若不存在,则f(i)=0。试求出f(1…n)。
输入格式
第一行一个正整数 n。
第二行 n个正整数 a1…n。
输入:
5
1 4 2 3 5
输出
2 5 4 5 0
分析题意:这是一道单调栈的模板题,所以问法很直接,就是 求数组中的每个元素的右边第一个大于当前元素的元素下角标,那么就只需要在维护单调栈的过程中,用另外一个数组记录当前每个元素右边第一个大于它的下角标即可。不过有个需要注意的地方,那就是输入需要优化,如果只用cin那么只能得60pts,这里建议用scanf或者快读模板。或者像我一样加上一句iostream::sync_with_stdio(false);那么就能将cin优化到scanf的效率了。倘若不信,读者大可一试。
AC代码如下:
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e6+10;
int a[maxn],ans[maxn];
int main(){
iostream::sync_with_stdio(false);
int n;cin>>n;
stack<int>s;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
if(s.empty()||a[i]<=a[s.top()]) s.push(i);
else{
while(!s.empty()&&a[i]>a[s.top()]){
ans[s.top()]=i;
s.pop();
}
s.push(i);
}
}
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
return 0;
}
看到这,相信读者对单调栈已经有了一定了解,那么接下来看一道比较经典的单调栈题。
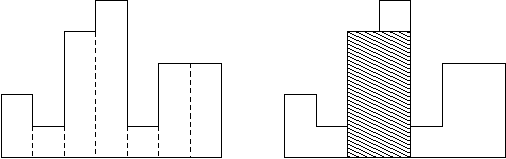
SP1805 HISTOGRA - Largest Rectangle in a Histogram
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
输入格式
无
输出格式
无
题意翻译
题目描述
如图所示,在一条水平线上有 n 个宽为 1 的矩形,求包含于这些矩形的最大子矩形面积(图中的阴影部分的面积即所求答案)。
输入格式:
有多组测试数据,每组数据占一行。输入零时读入结束。
每行开头为一个数字 n(1≤n≤1e5 ),接下来在同一行给出 n 个数字 h1,h2?,?,hn(0≤hi≤1e9 ),表示每个矩形的高度。
输出格式:
对于每组数据,输出最大子矩阵面积,一组数据输出一行。
输入输出样例
输入:
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出:
8
4000
分析题目:
一看到这道题,估计大家第一想法就是暴力枚举,用三重for循环枚举高和宽,然后遍历答案,显然时间复杂度为O(n^3)是一定会超时的,当然也是可以优化到O(n ^2),但由于n<=1e5,依旧会超时,所以就得换种方法。此时仔细分析矩形,为了让每一个矩形的高度都能够遍历到,我们不妨来维护一个单调递减栈(从栈顶到栈底的元素单调递减),1:只有在栈为空或者当前元素大于栈顶元素时,将当前元素入栈;并且用一个宽度数组w[maxn]记录可以以它为矩形高的连续宽度。2,否则如果当前元素小于栈顶元素,则将栈顶元素出栈,一直到栈为空或者当前元素大于栈顶元素,并且累计每次出栈的元素的宽度,再乘上出栈元素的高用来更新最大矩形面积;3.最后将当前元素入栈并更新它的宽度(即为之前弹出的所有元素累计宽度加1)。一直重复1~3步,直至遍历结束。

AC代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100010;
int n;
ll a[maxn],w[maxn];
ll ans;
int main()
{
while(cin>>n&&n)
{
stack<int>s;
ans=0;
for(int i=1;i<=n;i++) cin>>a[i];
a[n+1]=0;
for(int i=1;i<=n+1;i++)
{
if(s.empty()||a[i]>a[s.top()]) s.push(i),w[i]=1;
else{
ll width=0;
while(!s.empty()&&a[s.top()]>a[i])
{
width+=w[s.top()];
ans=max(ans,width*a[s.top()]);
s.pop();
}
s.push(i),w[i]=width+1;
}
}
cout<<ans<<endl;
}
}
对顶堆
基本概念:是由两个优先队列(堆)共同维护形成的一种特殊的数据结构(此定义不具有官方权威性,纯属是笔者的想法)。
实际作用:动态维护一个序列中第k大或者第k小的值(即可以维护序列的中位数)。
效率: 由于在维护对顶堆过程中,所有数据最多进出队列两次,并且只有少数数据到达两次(其他大部分数据只会进出一次),所以时间复杂度为O(n).由于整个维护过程是基于堆进行的,所以整体时间复杂度为O(nlogn).
大致图形:
以上两个图形一个为大根堆(降序的优先队列),一个为小根堆(升序的优先队列)。
用途一:维护序列中第k大的值
分析:要想维护序列中第k大的数,我们可以让小根堆的大小等于k,并且让小根堆里的最小数都大于大根堆里的最大数,此时小根堆的堆顶(即优先队列队首)就是所需答案。那么,我们应该如何一步一步维护它呢?仔细想想后不难发现,我们可以首先往小根堆里插入第一个元素,然后对于接下来的元素,如果此时的元素大于小根堆队首,则插入小根堆中;否则,插入到大根堆中。这样,就可以很轻松的实现小根堆里的最小数大于大根堆里的最大数。不过要注意边界判断,如果小根堆的数据个数不等于k,那么就要分类讨论;第一类,小根堆的数据个数小于k,那么就将大根堆的最大数(队首)插入小根堆,然后大根堆弹出;第二类,小根堆的数据个数大于k,那么就将小根堆的最小数(队首)插入大根堆,然后小根堆弹出。
模板代码:
priority_queue<int>q1; //大根堆(自动降序)
priority_queue<int,vector<int>,greater<int> >q2; //小根堆(自动升序)
for(int i=1;i<=n;i++){ //输入n个数
cin>>x;
if(q2.empty()||x>q2.top()) q2.push(x);
else q1.push(x);
}
while(!q2.empty()&&q2.size()!=k){
if(q2.size()>k) {q1.push(q2.top());q2.pop();}
if(q2.size()<k) {q2.push(q1.top());q1.pop();}
}
了解到这,那就写道例题练练手吧!!!
题目描述
给出一个长度为N(N<=100000)的非负整数序列Ai,对于所有1≤k≤(N+1)/2,输出A1,A1~A3,…,A1 ~A(2k-1)的中位数。即前1,3,5,…个数的中位数。
输入格式
第1行为一个正整数N,表示了序列长度。
第2行包含N个非负整数Ai (Ai ≤ 10^9)。
输出格式
共(N+1)/2行,第i行为A1,A3,…,A 2k?1 的中位数。
输入输出样例
输入
7
1 3 5 7 9 11 6
输出
1
3
5
6
分析:很显然,这是一道连续求序列中位数的题,我们只需要将中位数也就是第(1+i)/2为当作k,就变成了一道连续维护序列第k大的值的对顶堆模板题。遍历细节:每次在i是奇数的时候输出值。
AC代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
iostream::sync_with_stdio(false);
int n,x,mid;
priority_queue<int>q1; //大根堆
priority_queue<int,vector<int>,greater<int> >q2; //小根堆
cin>>n;
for(int i=1;i<=n;i++){
cin>>x;mid=(i+1)/2;
if(q2.empty()||x>q2.top()) q2.push(x);
else if(x<q2.top()) q1.push(x);
if(i&1){
while(!q2.empty()&&q2.size()!=mid){
if(q2.size()>mid) {q1.push(q2.top());q2.pop();}
if(q2.size()<mid) {q2.push(q1.top());q1.pop();}
}
cout<<q2.top()<<endl;
}
}
return 0;
}
用途二:维护序列中第k小的值
分析:要想维护序列中第k小的数,我们可以大根堆的大小等于k,并且让小根堆里的最小数都大于大根堆里的最大数,此时大根堆的堆顶(即优先队列队首)就是所需答案。那么,我们应该如何一步一步维护它呢?仔细想想后不难发现,我们可以首先往大根堆里插入第一个元素,然后对于接下来的元素,如果此时的元素小于大根堆队首,则插入大根堆中;否则,插入到小根堆中。这样,就可以很轻松的实现小根堆里的最小数大于大根堆里的最大数。不过要注意边界判断,如果大根堆的数据个数不等于k,那么就要分类讨论;第一类,大根堆的数据个数小于k,那么就将小根堆的最小数(队首)插入大根堆,然后小根堆弹出;第二类,大根堆的数据个数大于k,那么就将大根堆的最大数(队首)插入小根堆,然后大根堆弹出。
模板代码:
priority_queue<int>q1; //大根堆(自动降序)
priority_queue<int,vector<int>,greater<int> >q2; //小根堆(自动升序)
for(int i=1;i<=n;i++){ //输入n个数
cin>>x;
if(q1.empty()||x>q1.top()) q1.push(x);
else q2.push(x);
}
while(!q1.empty()&&q1.size()!=k){
if(q1.size()>k) {q2.push(q1.top());q1.pop();}
if(q1.size()<k) {q1.push(q2.top());q2.pop();}
}
当然为了巩固知识也来一道经典例题
UVA501 Black Box
Description 我们使用黑匣子的一个简单模型。它能存放一个整数序列和一个特别的变量i。在初始时刻,黑匣子为空且i等于0。这个黑匣子能执行一系列的命令。有两类命令: ADD(x):把元素x放入黑匣子; GET:把i加1的同时,输出黑匣子内所有整数中第i小的数。牢记第i小的数是当黑匣子中的元素已非降序排序后位于第i位的元素。 下面是一个11个命令的例子:
编号 命令 i 黑匣子内容
输出
1 ADD(3) 0 3
2 GET 1 3 3
3 ADD(1) 1 1,3
4 GET 2 1,3 3
5 ADD(-4) 2 -4,1,3
6 ADD(2) 2 -4,1,2,3
7 ADD(8) 2 -4,1,2,3,8
8 ADD(-1000) 2 -1000,-4,1,2,3,8
9 GET 3 -1000,-4,1,2,3,8 1
10 GET 4 -1000,-4,1,2,3,8 2
11 ADD(2) 4 -1000,-4,1,2,2,3,8
现需要一个有效的算法处理给定的一系列命令。ADD和GET命令的总数至多个有30000个。 定义ADD命令的个数为M个,GET命令的个数为N个。 我们用下面得两个整数序列描述命令序列1.A(1),A(2),……,A(M):加入黑匣子的元素序列。所有的数均为绝对值不超过2000000的整数。例如在上例中A=(3,1,-4,2,8,-1000,2)。 2.u(1),u(2),……,u(N):u(i)表示第i个GET命令在第u(i)个ADD命令之后,例如在上例中,u=(1,2,6,6)。 你可以假定自然数序列u(1),u(2),……,u(N)以非降序排列,N≤M,且对于每一个p(1≤p≤N)有p≤u§≤M 现在要求找出对于给定的命令串的最好的处理方法。ADD 和 GET 命令分别最多有30000个。 现在用两个整数数组来表示命令串:
A(1), A(2), …, A(M): 一串将要被放进Black Box的元素。每个数都是绝对值不超过2 000 000 000 的整数 M <= 30000。例如上面的例子就是1.A=(3, 1, -4, 2, 8, -1000, 2).
u(1), u(2), …, u(N): 表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(1, 2, 6, 6). 输入数据不用判错。 2.Input 题目有多组输入数据! 第一行是一个表示输入组数的整数 N ,隔一空行之后是 N 组输入数据,每组输入数据之间都有一行空行隔开,各组数据都是按上面的形式输入。 Output 输出包含 N 组输出数据,每一组之间用一个空行隔开。
输入输出样例
输入:
1
7 4
3 1 -4 2 8 -1000 2
1 2 6 6
输出:
3
3
1
2
本题题意较难理解,但是由于本题十分经典,望读者耐心思考。
分析:由于是一道求第k小的数的题,显然要用对顶堆,但是应该如何用呢?怎么让输入的两个数组建立联系才是关键,于是就有了笔者下面代码的一个双重for循环,由于数据小于30000,所以是不会超时的,望读者好好理解这个双重for循环。
#include<bits/stdc++.h>
using namespace std;
const int maxn=30005;
int t,m,n,a[maxn],u[maxn],pos;
int main(){
iostream::sync_with_stdio(false);
cin>>m>>n;
priority_queue<int>q1; //大根堆降序
priority_queue<int,vector<int>,greater<int> >q2; //小根堆升序
pos=0;
for(int i=1;i<=m;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>u[i];
for(int i=1;i<=n;i++){
for(int j=u[i-1]+1;j<=u[i];j++){
if(q1.empty()||a[j]<q1.top()) q1.push(a[j]);
else q2.push(a[j]);
}
while(!q1.empty()&&q1.size()!=i){
if(q1.size()<i) {q1.push(q2.top());q2.pop();}
if(q1.size()>i) {q2.push(q1.top());q1.pop();}
}
cout<<q1.top()<<endl;
}
return 0;
}
看到这相信对顶堆你已经很了解了,那么别忘了三连击啊!!!