1.标题统计
题目描述
凯凯刚写了一篇美妙的作文,请问这篇作文的标题中有多少个字符?
注意:标题中可能包含大、小写英文字母、数字字符、空格和换行符。统计标题字符数时,空格和换行符不计算在内。
输入格式
输入文件只有一行,一个字符串s。
输出格式
输出文件只有一行,包含一个整数,即作文标题的字符数(不含空格和换行符)。
样例输入
234
样例输出
3
样例输入
Ca 45
样例输出
4
问题提示
【输入输出样例1说明】
标题中共有3个字符,这3个字符都是数字字符。
【输入输出样例2说明】
标题中共有5个字符,包括1个大写英文字母,1个小写英文字母和2个数字字符,还有1个空格。由于空格不计入结果中,故标题的有效字符数为4个。
【数据规模与约定】
规定?|s|?表示字符串s的长度(即字符串中的字符和空格数)。
对于40%?的数据,1?≤|s|≤?5,保证输入为数字字符及行末换行符。
对于80%?的数据,1≤|s|≤5,输入只可能包含大、小写英文字母、数字字符及行末换行符。
对于100%?的数据,1≤|s|≤5,输入可能包含大、小写英文字母、数字字符、空格和行末换行符。
#include <cstdio>
char c;
int cnt;
int main() {
?? ?while (c = getchar()) {
?? ??? ?if (c == EOF || c == '\n') break;
?? ??? ?if (c != ' ') cnt ++;
?? ?}
?? ?printf("%d\n", cnt);
?? ?return 0;
}
2.龙虎斗
题目描述
轩轩和凯凯正在玩一款叫《龙虎斗》的游戏,游戏的棋盘是一条线段,线段上有n个兵营(自左至右编号1~n),相邻编号的兵营之间相隔1厘米,即棋盘为长度为n?1厘米的线段。i号兵营里有ci位工兵。
下面图1为?n=6?的示例:

图1. n=6的示例
轩轩在左侧,代表“龙”;凯凯在右侧,代表“虎”。他们以m号兵营作为分界,靠左的工兵属于龙势力,靠右的工兵属于虎势力,而第m号兵营中的工兵很纠结,他们不属于任何一方。
一个兵营的气势为:该兵营中的工兵数??该兵营到m号兵营的距离;参与游戏一方的势力定义为:属于这一方所有兵营的气势之和。
下面图2为?n=6,m=4?的示例,其中红色为龙方,黄色为虎方:

?n=6,m=4的示例
游戏过程中,某一刻天降神兵,共有s1位工兵突然出现在了p1号兵营。作为轩轩和凯凯的朋友,你知道如果龙虎双方气势差距太悬殊,轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续,你需要选择一个兵营p2,并将你手里的s2位工兵全部派往兵营p2,使得双方气势差距尽可能小。
注意:你手中的工兵落在哪个兵营,就和该兵营中其他工兵有相同的势力归属(如果落在m号兵营,则不属于任何势力)。
输入格式
输入文件名为fight.in。
输入文件的第一行包含一个正整数n,代表兵营的数量。
接下来的一行包含n个正整数,相邻两数之间以一个空格分隔,第i个正整数代表编号为�?的兵营中起始时的工兵数量ci。
接下来的一行包含四个正整数,相邻两数间以一个空格分隔,分别代表m,p1,s1,s2。
输出格式
输出文件名为fight.out
输出文件有一行,包含一个正整数,即p2,表示你选择的兵营编号。如果存在多个编号同时满足最优,取最小的编号。
样例输入
6
2 3 2 3 2 3
4 6 5 2
样例输出
2
样例输入
6
1 1 1 1 1 16
5 4 1 1
样例输出
1
问题提示
【输入输出样例1说明】
见问题描述中的图2。
双方以?m=4?号兵营分界,有s1=5?位工兵突然出现在?p1=6?号兵营。
【输入输出样例2说明】
双方以?m=5?号兵营分界,有s1=1?位工兵突然出现在?p1=4?号兵营。
此时可以使双方气势的差距最小。
【数据规模与约定】
1<m<n,1≤p1≤n。
对于20%?的数据,n=3,m=2,ci=1,s1,s2≤100。
另有20%?的数据,n≤10,p1=m,ci=1,s1,s2≤100。
对于60%?的数据,n≤100,ci=1,s1,s2≤100。
对于80%?的数据,n≤100,ci,s1,s2≤100。
对于100%?的数据,n≤105,ci,s1,s2≤109。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int n, m, p1, p2;
long long a[maxn], s1, s2, sum;
int main() {
?? ?cin >> n;
?? ?for (int i = 1; i <= n; i ++) cin >> a[i];
?? ?cin >> m >> p1 >> s1 >> s2;
?? ?a[p1] += s1;
?? ?p2 = 1;
?? ?for (int i = 1; i <= n; i ++)
?? ??? ?sum += ( (long long) (i - m) ) * a[i];
?? ?for (int i = 1; i <= n; i ++)
?? ??? ?if ( abs(sum + (i-m) * s2) < abs(sum + (p2-m) * s2) ) p2 = i;
?? ?cout << p2 << endl;
?? ?return 0;
}
3.摆渡车
题目描述
有n名同学要乘坐摆渡车从人大附中前往人民大学,第i位同学在第ti分钟去等车。只有一辆摆渡车在工作,但摆渡车容量可以视为无限大。摆渡车从人大附中出发、把车上的同学送到人民大学、再回到人大附中(去接其他同学),这样往返一趟总共花费m分钟(同学上下车时间忽略不计)。摆渡车要将所有同学都送到人民大学。
凯凯很好奇,如果他能任意安排摆渡车出发的时间,那么这些同学的等车时间之和最小为多少呢?
注意:摆渡车回到人大附中后可以即刻出发。
输入格式
第一行包含两个正整数n、m,以一个空格分开,分别代表等车人数和摆渡车往返一趟的时间。
第二行包含n个正整数,相邻两数之间以一个空格分隔,第i个非负整数ti代表第i个同学到达车站的时刻。
输出格式
输出一行,一个整数,表示所有同学等车时间之和的最小值(单位:分钟)。
样例输入
5 1
3 4 4 3 5
样例输出
0
样例输入
5 5
11 13 1 5 5
样例输出
4
问题提示
【输入输出样例1说明】
同学1和同学4在第3分钟开始等车,等待0分钟,在第3分钟乘坐摆渡车出发。摆渡车在第4分钟回到人大附中。
同学2和同学3在第4分钟开始等车,等待0分钟,在第4分钟乘坐摆渡车出发。摆渡车在第5分钟回到人大附中。
同学5在第5分钟开始等车,等待0分钟,在第5分钟乘坐摆渡车出发。自此所有同学都被送到人民大学。总等待时间为0。
【输入输出样例2说明】
同学3在第1分钟开始等车,等待0分钟,在第1分钟乘坐摆渡车出发。摆渡车在第6分钟回到人大附中。
同学4和同学5在第5分钟开始等车,等待1分钟,在第6分钟乘坐摆渡车出发。摆渡车在第11分钟回到人大附中。
同学1在第11分钟开始等车,等待2分钟;同学2在第13分钟开始等车,等待0分钟。他/她们在第13分钟乘坐摆渡车出发。自此所有同学都被送到人民大学。总等待时间为4。可以证明,没有总等待时间小于4的方案。
【数据规模与约定】
对于10%?的数据,n≤10,?m=1,?0≤ti≤100。
对于30%?的数据,n≤120,?m≤2,?0≤ti≤100。
对于50%?的数据,n≤500,?m≤100,?0≤ti≤104。
另有20%?的数据,n≤500,?m≤10,?0≤ti≤4×106。
对于100%?的数据,n≤500,?m≤100,?0≤ti≤4×106。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 4000400;
int n, m, t, maxt;
long long f[maxn], cnt[maxn];
int main() {
?? ?cin >> n >> m;
?? ?for (int i = 0; i < n; i ++) {
?? ??? ?cin >> t;
?? ??? ?cnt[t] ++;
?? ??? ?if (t > maxt) maxt = t;
?? ?}
?? ?for (int i = 0; i <= maxt + m; i ++) {
?? ??? ?long long tmp = 0;
?? ??? ?for (int j = 0; j < m && i-j >=0; j ++) {
?? ??? ??? ?tmp += cnt[i-j] * ( (long long) j );
?? ??? ?}
?? ??? ?f[i] = tmp;
?? ??? ?if (i >= m) f[i] += f[i-m];
?? ??? ?for (int j = m+1; j <= 2*m && i - j >= 0; j ++) {
?? ??? ??? ?tmp += cnt[i-j+1] * ( (long long) (j-1) );
?? ??? ??? ?if (f[i-j] + tmp <= f[i]) f[i] = f[i-j] + tmp;
?? ??? ?}
?? ?}
?? ?long long ans = f[maxt];
?? ?for (int i = 1; i <= m; i ++) {
?? ??? ?ans = min(ans, f[maxt+i]);
?? ?}
?? ?cout << ans << endl;
?? ?return 0;
}
4.对称二叉树
题目描述
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
1.?二叉树;
2.?将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值,节点外的?id表示节点编号。

现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点?TT?为子树根的一棵“子?树”指的是:节点T和它的全部后代节点构成的二叉树。
输入格式
第一行一个正整数n,表示给定的树的节点的数目,规定节点编号1n,其中节点1是树根。
第二行n个正整数,用一个空格分隔,第?i个正整数vi?代表节点i的权值。
接下来n行,每行两个正整数li, ri??,分别表示节点i的左右孩子的编号。如果不存在左/右孩子,则以?-1表示。两个数之间用一个空格隔开。
输出格式
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
样例输入
2
1 3
2 -1
-1 -1
样例输出
1
样例输入
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8
样例输出
3
问题提示
【输入输出样例1说明】
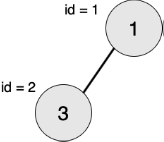
最大的对称二叉子树为以节点2?为树根的子树,节点数为1。
【输入输出样例2说明】

最大的对称二叉子树为以节点7?为树根的子树,节点数为3。
【数据规模与约定】
共25个测试点。
vi?≤?1000。
测试点1~3,n≤10,保证根结点的左子树的所有节点都没有右孩子,根结点的右子树的所有节点都没有左孩子。
测试点4~8,n≤10。
测试点9~12,n≤105,保证输入是一棵“满二叉树”。
测试点13~16,n≤105,保证输入是一棵“完全二叉树”。
测试点17~20,n≤105,保证输入的树的点权均为1。
测试点21~25,n≤106。
本题约定:
层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一节点的层次等于其父亲节点的层次加1。
树的深度:树中节点的最大层次称为树的深度。
满二叉树:设二叉树的深度为h,且二叉树有2h-1个节点,这就是满二叉树。
#include<cstdio>
inline int max(int x, int y)
{
?? ?return x > y ? x : y;
}
const int MAXN = 1000000;
int cnt[MAXN + 5], lef[MAXN + 5], rig[MAXN + 5], ans;
int v[MAXN + 5]; // 节点的权值
// 检查左右子树是否对称
bool checkSym(int leftId, int rightId)
{
? ? if(leftId == -1 && rightId == -1)
? ? {
? ? ? ? // 若左右子节点都不存在,则认为是对称
? ? ? ? return true;
? ? }
?? ?if(v[leftId] != v[rightId])
? ? {
? ? ? ? // 左子节点值 不等于 右子节点值,说明不对称
? ? ? ? return false;
? ? }
?? ?else
? ? {
? ? ? ? // 左子节点值等于右子节点值,则左左=右右且右左=左右,说明对称;否则不对称。注意要递归下去
? ? ? ? return checkSym(lef[leftId], rig[rightId]) && checkSym(rig[leftId], lef[rightId]);
? ? }
}
// 求第nodeId个节点为根节点的二叉树,所包含的节点总数
int nodeCnt(int nodeId)
{
? ? // 当前节点不存在
?? ?if(-1 == nodeId)
? ? {
? ? ? ? return 0;
? ? }
?? ?else
? ? {
? ? ? ? // 左子树节点数 + 右子树节点树 + root本身的节点数1
? ? ? ? return cnt[nodeId] = nodeCnt(lef[nodeId]) + nodeCnt(rig[nodeId]) + 1;
? ? }
}
void dfs(int nodeId)
{
? ? // 空节点为递归终止的条件
?? ?if(-1 == nodeId)
? ? {
? ? ? ? return;
? ? }
? ? // 左子树节点总数 等于 右子树节点总数,这是对称的前提
?? ?if(cnt[lef[nodeId]] == cnt[rig[nodeId]])
? ? {
? ? ? ? if(checkSym(lef[nodeId], rig[nodeId]))
? ? ? ? {
? ? ? ? ? ? // 若对称,获取总的节点数,并与原先的ans比较
? ? ? ? ? ? ans = max(ans, cnt[nodeId]);
? ? ? ? }
? ? }
? ? // 左子树下是否包含对称二叉树
?? ?dfs(lef[nodeId]);
?? ?// 右路子树是否包含对称二叉树
? ? dfs(rig[nodeId]);
}
int main()
{
?? ?int n;
?? ?scanf("%d", &n);
?? ?for(int i=1; i<=n; i++)
? ? {
? ? ? ? scanf("%d", &v[i]);
? ? }
?? ?for(int i=1; i<=n; i++)
? ? {
?? ??? ?scanf("%d%d", &lef[i], &rig[i]);
?? ?}
?? ?nodeCnt(1);
?? ?dfs(1);
?? ?printf("%d\n", ans);
?? ?return 0;
?? ?}?
点赞关注!!!
 +
+
?=======================??
?happy !!!
?
?