视公开课链接
本文旨在记录课程的核心内容和笔者的思考
Ch1.计算机系统漫游
C编译(ccl)与链接(ld)
Switch是否总时比if-else高效?
while循环总比for循环高效么?
指针引用比数组高效么?
函数的本地临时变量为什么比入参的引用更高效?
算数表达式的括号也能影响运算速度?
Ch2.信息的表示和处理
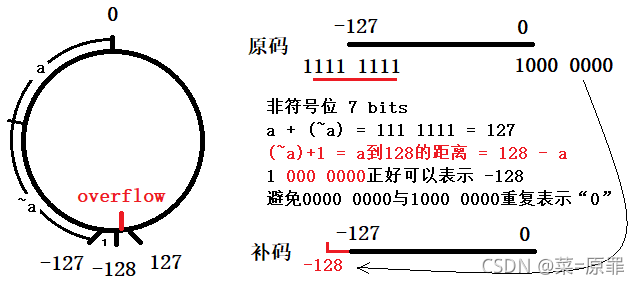
Integer – 补码与符号位
事实上,有符号数(two’s complement,补码)的符号位,是具有权重的,只不过需要取反,如-2表示为
1111
,
1110
=
?
2
7
+
∑
w
=
1
w
=
6
2
w
+
0
?
2
w
=
0
=
?
2
1111,1110=\red {-2^7}+\sum_{\red {w=1}}^{w=6}2^w+0*2^{\red {w=0}}=-2
1111,1110=?27+∑w=1w=6?2w+0?2w=0=?2
- T 2 U ( x ) = B 2 U ( T 2 B ( x ) ) = u x T2U(x) = B2U(T2B(x))=ux T2U(x)=B2U(T2B(x))=ux
- U 2 T ( u x ) = B 2 T ( U 2 B ( x ) ) = x U2T(ux) = B2T(U2B(x))=x U2T(ux)=B2T(U2B(x))=x
- T M I N = ? T M A X ? 1 T_{MIN}=-T_{MAX}-1 TMIN?=?TMAX??1
- U M A X = 2 × T M A X + 1 = 01111 < < 1 + 1 U_{MAX}=2\times T_{MAX}+1=01111<<1+1 UMAX?=2×TMAX?+1=01111<<1+1
" u x ux ux and x x x have same bit pattern,just a bunch of bits to computer itself."
//sizeof return unsigned int, cast a into unsigned, you got stuck forever
for(int a=1;a-sizeof(a)>=0;a--)
//so be care of unsigned "i" used for array in case a[i]
//i=0; i--=UMAX; a[i] may cause out of bounds
int main()
{
unsigned int a=numeric_limits<unsigned int>::max();
int b=-1;
unsigned int c=-3;
cout<<(int)a<<" "<<a<<endl; //-1 4294967295
cout<<(b==a?"True":"Flase")<<endl; //True
cout<<(b>a?"True":"Flase")<<endl; //Flase
cout<<std::hex<<c<<" "<<-c<<" "<<c+(-c)<<endl; //fffffffd 3 0
cout<<std::hex<<b<<"\n"<<numeric_limits<int>::max()<<endl; //ffffffff 7fffffff
cout<<b+numeric_limits<int>::max()<<endl; //7ffffffe
return 0;
}
符号位扩展/截断
sign bit shifts left, others remain
0110
=
?
0
×
2
3
+
1
×
2
2
+
1
×
2
1
+
0
×
2
0
=
6
0110 = -0\times2^{3}+1\times2^{2}+1\times2^{1}+0\times2^{0}=6
0110=?0×23+1×22+1×21+0×20=6
1110
=
?
1
×
2
3
+
1
×
2
2
+
1
×
2
1
+
0
×
2
0
=
?
2
1110 = -1\times2^{3}+1\times2^{2}+1\times2^{1}+0\times2^{0}=-2
1110=?1×23+1×22+1×21+0×20=?2
11110
=
?
1
×
2
4
+
1
×
2
3
+
1
×
2
2
+
1
×
2
1
+
0
×
2
0
=
?
1
×
2
3
+
1
×
2
2
+
1
×
2
1
+
0
×
2
0
=
?
2
11110 = \red{-1\times2^{4}+1\times2^{3}}+1\times2^{2}+1\times2^{1}+0\times2^{0}=\red{-1\times2^{3}}+1\times2^{2}+1\times2^{1}+0\times2^{0}=-2
11110=?1×24+1×23+1×22+1×21+0×20=?1×23+1×22+1×21+0×20=?2
Floating point – IEEE 754 (1985)
Numerical Form
( ? 1 ) s M × 2 E (-1)^{s}M\times2^{E} (?1)sM×2E
| precision | sign field | exp field | frac field |
|---|---|---|---|
| value | s | exp | frac |
| single | 1 bit | k = 8 bit | 23 bit |
| double | 1bit | k = 11 bit | 52 bit |
Extended precision 英特尔特用 | 1 bit |15 bit | 64 bit
共10字节,对齐16字节,因此后6字节为空
Normalized Values
e x p ≠ 000...0 exp \neq 000...0 exp?=000...0 or 111...1 111...1 111...1
-
E
=
e
x
p
?
(
2
k
?
1
?
1
)
E = exp - (2^{k-1}-1)
E=exp?(2k?1?1)
single E ∈ [ ? 126 , 127 ] E\in[-126,127] E∈[?126,127]
double E ∈ [ ? 1022 , 1023 ] E\in[-1022,1023] E∈[?1022,1023] - M = 1.11.. . 2 M = 1.11..._2 M=1.11...2?