T1:问题 A: 一元三次方程的解
题目描述
设-元三次方程ax3+bx2+cx+d=0,给出该方程中各项系数a、b、c、d(均为实数),并假设该访程一定存在3个不同的实数解(范围在-100~ 100之间),且解与解之差的绝对值大于或等于1,请编程求出这3个解。
输入
1行4个数,依次表示a、b、c、d的值。
输出
1行3个数,表示方程的3个解,之间用1个空格隔开。请从小到大输出,精确到小数点后2位。
样例输入
1 -5 -4 20
样例输出
-2.00 2.00 5.00
题解
对于这道题,已经明确表示有3个解,因此我们考虑枚举每一个x,在确定精度的情况下,利用零点判定定理来得到答案。
参考代码
#include<cstdio>
using namespace std;
double a,b,c,d;
double figure(double x)
{
return a*x*x*x+b*x*x+c*x+d;
}
int main()
{
scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
for(double i=-100.0001;i<100.0000;i+=0.0001)
{
if((figure(i)>=0&&figure(i+0.0001)<=0)||(figure(i)<=0&&figure(i+0.0001)>=0))
printf("%.2lf ",i);
}
return 0;
}T2:问题 B: 单词查找树
题目描述
????在进行文法分析的时候,通常需要检测一个单词是否在我们的单词列表里。为了提高查找和定位的速度,通常都画出与单词列表所对应的单词查找树,其特点如下:
??????1.根结点不包含字母,除根结点外每一个结点都仅包含一个大写英文字母。
???? ?2.从根结点到某一结点,路径上经过的字母依次连起来所构成的字母序列,称为该结点对应的单词。单词列表中的每个单词,都是该单词查找树某个结点所对应的单词。
??????3.在满足上述条件下,该单词查找树的结点数最少。
????? 4.例如下图左边的单词列表就对应于右边的单词查找树。注意,对一个确定的单词列表,请统计对应的单词查找树的结点数(包含根结点)。
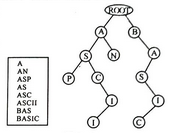
?
输入
一个单词列表,每一行仅包含一个单词和一个换行/回车符。每个单词仅由大写的英文字母组成,长度不超过63个字母。输入文件总长度不超过32K,至少有一行数据。(注意:测试数据通过输入文件提供,在OJ上提交的程序无须使用文件操作相关函数。)
输出
仅包含一个整数,该整数为单词列表对应的单词查找树的结点数。
样例输入
A
AN
ASP
AS
ASC
ASCII
BAS
BASIC
样例输出
13
题解
这道题考察的是对字典树的理解。其实我们会发现,我们所求的答案正是字典树上的节点总数。
参考代码
#include<cstdio>
#include<cstring>
using namespace std;
struct trie
{
int num;
int son[30];
}a[100001];
int t=1,p,len;
char x[120000];
void make_tree()
{
p=0;
len=strlen(x);
for(int i=0;i<len;i++)
{
if(!a[p].son[x[i]-'A']) a[p].son[x[i]-'A']=++t;
p=a[p].son[x[i]-'A'];
}
}
int main()
{
while(scanf("%s",x)!=EOF)
make_tree();
printf("%d",t);
return 0;
}T3:问题 C: 比例简化
题目描述
????在社交媒体上,经常会看到针对某一个观点同意与否的民意调查以及结果,例如,对某一观点表示支持的有1498?人,反对的有902人,那么赞同与反对的比例可以简单地记为1498?:902。
????不过,如果把调查结果就以这种方式呈现出来,大多数人肯定不会满意。因为这个比例的数值太大,难以一眼看出它们的关系。对于上面这个例子,如果把比例记为5:3,虽然与真实绪果有一定的误差,但依然能够较为准确地反映调查结果,同时也显得比较直观。
????现给出支持人数A,反对人数B,以及一个上限L,请将A比B化简为A'比B'?,要求在A'和B'均不大于L且A'和B'互质(两个整数的最大公约数是1)的前提下,A'?/B'>?A/B且A'?/B'?-A/B的值尽可能小。
输入
?一行三个正整数A、B、L,每两个正整数之间用一个空格隔开,分别表示支持人数.反对人数以及上限。其中,1≤A≤1000000,1≤B≤1000000,1≤L≤100,A/B≤L。
输出
一行两个正整数A’和B’,中间用一个空格隔开,表示化简后的比例。
样例输入
1498 902 10
样例输出
5 3
题解
该题难度不大,但是需要注意细节,即A’/B’>A/B且A’/B’-A/B尽可能的小。由于L范围不大,因此可以考虑枚举每一个A’,B’来依次比较以获得答案。
参考代码
#include<cstdio>
using namespace std;
int a,b,a1,b1,l;
int gcd(int m,int n)
{
return n==0?m:gcd(n,m%n);
}
double minn=999999999.0;
int main()
{
scanf("%d%d%d",&a,&b,&l);
for(int i=1;i<=l;i++)
{
for(int j=1;j<=l;j++)
{
if(gcd(i,j)==1)
if(double(i)/double(j)>double(a)/double(b))
{
if(double(i)/double(j)-double(a)/double(b)<minn)
{
a1=i;b1=j;
minn=double(i)/double(j)-double(a)/double(b);
}
}
}
}
printf("%d %d",a1,b1);
return 0;
}T4:问题 D: 幸运数的划分
题目描述
????判断一个正整数n是否能被一个“幸运数”整除。幸运数是指一个只包含4或7的正整数,如7、47、477等都是幸运数,17、42则不是幸运数。
输入
????一行一个正整数n,1≤n≤1000。
输出
????一行一个字符串,如果能被幸运数整除输出“YES”;否则,输出“NO”。
样例输入
47
样例输出
YES
题解
完全就是签到题。幸运数只有不到20个,无论是打表还是枚举,效率都过得去。
参考代码
#include<cstdio>
using namespace std;
int p[15]={0,4,44,444,7,77,777,47,74,447,474,744,747,774,477};
int n,pd=0;
int main()
{
scanf("%d",&n);
for(int i=1;i<=14;i++)
{
if(n%p[i]==0) pd=1;
}
if(pd==1) printf("YES");
else printf("NO");
}T5:最小花费
题目描述
????在n个人中,某些人的银行账号之间可以互相转账。这些人之间转账的手续费各不相同。给定这些人之间转账时需要从转账金额里扣除百分之几的手续费,请问A最少需要多少钱使得转账后B收到100元?
输入
??? 第1行输人两个正整数n、m,分别表示总人数和可以互相转账的人的对数。
??? 以下m行每行输入三个正整数x、y、z,表示标号为x的人和标号为y的人之间互相转账需要扣除z%的手续费(z<100)。
??? 最后一行输人两个正整数A、B。数据保证A与B之间可以直接或间接地转账。
输出
????输出A使得B到账100元最少需要的总费用。精确到小数点后8位。
样例输入
3 3
1 2 1
2 3 2
1 3 3
1 3
样例输出
103.07153164
提示
【数据范围】
1<=n<=2000
题解
这道题是考察最短路,我们可以从末尾往前推,找到一个最小的初始值,也可以从前往后推,找到一个最小的百分比。此处为第一种方式的代码。
参考代码
#include<cstdio>
#include<queue>
#include<iostream>
#include<cstring>
using namespace std;
struct tree
{
int nxt,to,dis;
}tr[1000000];
queue<int>q;
int head[1000000],vis[1000000],cnt=0,a,b;
double dp[1000000];
void build_tree(int u,int v,int d)
{
tr[++cnt].nxt=head[u];
tr[cnt].to=v;
tr[cnt].dis=d;
head[u]=cnt;
}
int n,m;
void bfs()
{
while(!q.empty())
{
int nus=q.front();q.pop();
vis[nus]=0;
for(int i=head[nus];i;i=tr[i].nxt)
{
int dis=tr[i].dis;
int to=tr[i].to;
if(dp[nus]/(double(100-dis)/100.0)<dp[to])
{
dp[to]=dp[nus]/(double(100-dis)/100.0);
if(!vis[to])
{
q.push(to);
vis[to]=1;
}
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) dp[i]=1e18;
for(int i=1;i<=m;i++)
{
int u,v,d;
scanf("%d%d%d",&u,&v,&d);
build_tree(v,u,d);
build_tree(u,v,d);
}
scanf("%d%d",&a,&b);
dp[b]=100.0;
q.push(b);
bfs();
printf("%.8lf",dp[a]);
return 0;
}T6:问题 F: 曹冲养猪
题目描述
自从曹冲搞定了大象以后,曹操就开始琢磨让儿子干些事业,于是派他到中原养猪场养猪,可是曹冲很不高兴,于是在工作中马马虎虎,有一次曹操想知道母猪的数量,于是曹冲想狠狠耍曹操一把。
举个例子,假如有 16 头母猪,如果建了 3 个猪圈,剩下 1 头猪就没有地方安家了;如果建造了 5 个猪圈,但是仍然有 1 头猪没有地方去;如果建造了 7 个猪圈,还有 2 头没有地方去。你作为曹总的私人秘书理所当然要将准确的猪数报给曹总,你该怎么办?
输入
第一行包含一个整数 n,表示建立猪圈的次数;
接下来 n 行,每行两个整数 ai?,bi?,表示建立了 ai? 个猪圈,有 bi? 头猪没有去处。你可以假定 ai?,aj? 互质。
输出
输出仅包含一个正整数,即为曹冲至少养猪的数目。
样例输入
3
3 1
5 1
7 2
样例输出
16
提示
【数据范围与提示】
对于全部数据,1≤n≤10,1≤bi?≤ai?≤1000。
题解
这道题是考察中国剩余定理,可以参考网上详解。
参考代码
?
#include<cstdio>
#define LL unsigned long long
using namespace std;
int cnt=0;
LL k,n=1ll,n1[1000001],m[1000001],mf[1000001],a[1000001],c[1000001];
LL mf1[1001],prime[1001],ak=0;
LL exgcd(LL a,LL b,LL & x,LL & y)
{
if(b==0) { x=1,y=1;return a; }
LL d=exgcd(b,a%b,x,y);
LL z=x;x=y;y=z-y*(a/b);
return d;
}
int main()
{
scanf("%lld",&k);
for(int i=1;i<=k;i++)
{
cnt++;
scanf("%lld%lld",&n1[cnt],&a[cnt]);
n*=n1[i];
}
//for(int i=1;i<=cnt;i++) printf("%lld ",a[i]);
for(int i=1;i<=cnt;i++)
{
m[i]=n/n1[i];
LL x,y;
exgcd(m[i],n1[i],x,y);
mf[i]=x=(x+n1[i])%n1[i];
c[i]=m[i]*mf[i];
}
LL x=0;
for(int i=1;i<=cnt;i++)
x=(x+c[i]*a[i])%n;
printf("%lld",x);
return 0;
}
?T7:问题 G: 保龄球
题目描述
??? 打保龄球是用一个滚球去打击十个站立的柱,将柱击倒。一局分十轮,每轮可滚球-次或多次,以击倒的柱数为依据计分。一局得分为十轮得分之和,而每轮的得分不仅与本轮滚球情况有关,还可能与后续一两轮的滚球情况有关。即某轮某次滚球击倒的柱数不仅要计入本轮得分,还可能会计人前一两轮得分。具体的滚球击柱规则和计分方法如下:
??? (1)若某一轮的第一次滚球就击倒全部十个柱,则本轮不再滚球(若是第十轮则还需另加两次滚球,不妨称其为第十一轮和第十二轮,并不是所有的情况都需要滚第十一轮和第十二轮球)。该轮得分为本次击倒柱数10与以后两次滚球所击倒柱数之和。
??? (2)若某一轮的第一次滚球未击倒十个柱,则可对剩下未倒的柱再滚球一次。如果这两次滚球击倒全部十个柱,则本轮不再滚球(若是第十轮则还需另加一次滚球), 该轮得分为这两次共击倒柱数10与以后一次滚球所击倒柱数之和。
??? (3)若某一轮两次滚球未击倒全部十个柱,则本轮不再继续滚球,该轮得分为这两次滚球击倒的柱数之和。
??? 总之,若某一轮中一次滚球或两次滚球击倒十个柱,则本轮得分是本轮首次滚球开始的连续三次滚球击倒柱数之和(其中有一次或两次不是本轮滚球)。若一轮内二次滚球击倒柱数不足十个,则本轮得分即为这两次击倒柱数之和。下面以实例说明如下:
轮?? ?????????? ?1???? ?2???? 3??? 4????? 5???? 6?????? 7???? ?8????? ?9????? 10??? 11??? 12
击球情况?? ? /???? ?/??? ? /???? 72??? 9/??? 81???? 8/??? ?/????? ?9/??? ??/????? 8/
各轮得分??? 30?? 27?? 19?? 9??? ?18??? 9???? ?20??? 20??? 20??? ?20
累计得分??? 30?? 57?? 76?? 85?? 103? 112? 132? 152? 172?? 192
??? 现在请编写一个保龄球计分程序,用来计算并输出最后的总得分。
输入
??? 输入一行,为前若干轮滚球的情况,每轮滚球用一到两个字符表示,每-个字符表示一次击球,字符“/”表示击倒当前球道上的全部的柱,否则用一个数字字符表示本次滚球击倒的当前球道上的柱的数目,两轮滚球之间用一个空格隔开。
输出
????输出-行一个整数,代表最后的得分。
样例输入
/ / / 72 9/ 81 8/ / 9/ / 8/
样例输出
192
题解
这道题第一个难点就是处理出每一次滚球的分数。比较简单的输入时直接输入字符串,然后通过判断空格后是否有东西来更新滚球个数cnt,比较麻烦的是判断10分,有两种情况:一种是第一次就10分,第二次就加起来10分。与其加标记,不如直接定义二维数组,第二位是0和1,表示第一次滚球分和第二次滚球分(如果第一次就10分,第二次默认为0),这样就能不重不漏。第二个难点是对于每一组滚球,我们要通过前后三次的分数来决定当前的总得分。这也是一个特判的过程,首先看总分是否为10,如果不为10,直接就是当前两次得分相加;如果是10,再看是不是一次就10分,如果是,就看下一次是不是10分,如果还是,就再加上下下次的第一轮(可能就是10分),否则,就直接当前10分加上下一次两次得分相加;如果当前第一轮不是10分,就当前两次再加上下一次的第一轮得分。
参考代码
#include<cstdio>
using namespace std;
char s[1000];
int a[1000][2],cnt=1,dis[1000],sum=0;
int main()
{
gets(s);
for(int i=0;i<=50;i++)
{
if(i==0)
{
if(s[i]=='/') a[1][0]=10;
else a[1][0]=s[i]-'0';
continue;
}
if(s[i]=='/'&&s[i-1]>='0'&&s[i-1]<='9')
a[cnt][1]=10-a[cnt][0];
if(s[i]=='/'&&s[i-1]==' ')
a[cnt][0]=10;
if(s[i]>='0'&&s[i]<='9'&&s[i-1]>='0'&&s[i-1]<='9')
a[cnt][1]=s[i]-'0';
if(s[i]>='0'&&s[i]<='9'&&s[i-1]==' ')
a[cnt][0]=s[i]-'0';
if(s[i]==' '&&s[i+1]!=' ') cnt++;
}
for(int i=1;i<=10;i++)
{
if(a[i][0]+a[i][1]==10)
{
if(a[i][0]==10)
{
if(a[i+1][0]==10)
dis[i]=20+a[i+2][0];
else dis[i]=10+a[i+1][0]+a[i+1][1];
}
else dis[i]=a[i][0]+a[i][1]+a[i+1][0];
}
else dis[i]=a[i][0]+a[i][1];
}
for(int i=1;i<=10;i++) sum+=dis[i];
printf("%d",sum);
return 0;
}T8:问题 H: 关押罪犯
题目描述
S城现有两座监狱,一共关押着N名罪犯,编号分别为1~N。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久,如果客观条件具备则随时可能爆发冲突。我们用“怨气值”(一个正整数值)来表示某两名罪犯之间的仇恨程度,怨气值越大,则这两名罪犯之间的积怨越多。如果两名怨气值为c的罪犯被关押在同一监狱,他们俩之间会发生摩擦,并造成影响力为c的冲突事件。每年年末,警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表,然后上报到S城Z市长那里。公务繁忙的Z市长只会去看列表中的第一个事件的影响力,如果影响很坏,他就会考虑撤换警察局长。在详细考察了N名罪犯间的矛盾关系后,警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配,以求产生的冲突事件影响力都较小,从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨,那么他们一定会在每年的某个时候发生摩擦。那么,应如何分配罪犯,才能使Z市长看到的那个冲突事件的影响力最小?这个最小值是多少?
输入
输入文件的每行中两个数之间用一个空格隔开。
第一行为两个正整数N和M,分别表示罪犯的数目以及存在仇恨的罪犯对数。
接下来的M行每行为三个正整数aj,bj,cj,表示aj号和bj号罪犯之间存在仇恨,其怨气值为cj。
数据保证1<=aj<=bj<=N,0<=cj<=1000000000,且每对罪犯组合只出现一次。
输出
输出文件共1行,为Z市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件,请输出0。
样例输入
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884
样例输出
3512
提示
分配方法:市长看到的冲突事件影响力是3512(由2号和3号罪犯引发)。其他任何分法都不会比这个分法更优。
对于30%的数据有N≤15。
对于70%的数据有N≤2000,M≤50000。
对于100%的数据有N≤20000,M≤100000。
题解
对于这道题,我开始的想法是建两科树,分别表示第一个监狱的所有人和第二个监狱的所有人。但是后来有了一种更简单的方法,就是把第一个人与第二个人的敌方大本营连在一起,第二个人和第一个人的敌方大本营连在一起。这样就能够用并查集一次性搞定。
参考代码
#include<cstdio>
#include<algorithm>
using namespace std;
struct node
{
int from,to,v;
}a[2000001];
int fa[500001];
int find(int v)
{
if(fa[v]==v) return v;
else return fa[v]=find(fa[v]);
}
int n,m,ans=0;
bool comp1(node p,node q)
{
return p.v>q.v;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n*2;i++) fa[i]=i;
for(int i=1;i<=m;i++)
scanf("%d%d%d",&a[i].from,&a[i].to,&a[i].v);
sort(a+1,a+m+1,comp1);
for(int i=1;i<=m;i++)
{
int l=find(a[i].from),r=find(a[i].to);
if(l==r)
{
ans=a[i].v;
break;
}
fa[find(a[i].from)]=find(a[i].to+n);
fa[find(a[i].to)]=find(a[i].from+n);
}
printf("%d",ans);
return 0;
}T8:问题 I: 暗黑游戏
题目描述
暗黑游戏中,装备直接决定玩家人物的能力。可以使用 Pg 和 Rune 购买需要的物品。暗黑市场中的装备,每件有不同的价格(Pg 和 Rune)、能力值、最大可购买件数。Kid 作为暗黑战网的一个玩家,当然希望使用尽可能少的 Pg 和 Rune 购买更优的装备,以获得最高的能力值。请你帮忙计算出现有支付能力下的最大可以获得的能力值。
输入
第一行,三个整数 N,P,R,分别代表市场中物品种类,Pg 的支付能力和 Rune 的支付能力。
第 2..N+1 行,每行四个整数,前两个整数分别为购买此物品需要花费的 Pg,Rune,第三个整数若为 0,则说明此物品可以购买无数件,若为其他数字,则为此物品可购买的最多件数(S),第四个整数为该装备的能力值。
输出
仅一行,一个整数,最大可获得的能力值。
样例输入
3 10 10
5 3 0 110
4 3 4 120
2 3 1 130
样例输出
370
题解
这是一道背包题。推荐的做法是01背包二进制优化加上完全背包。但是直接01背包也可以极限过。但是这道题还有一个新问题,就是一个物品会同时消耗两个值,这一点其实只需要在转移过程中多减一维就行,也就是说dp是2维的,分别对应2个消耗量。
参考代码
#include<cstdio>
#include<cstring>
using namespace std;
struct node {
int vp,vr,num,val;
} a[1010];
int n,p,r,dp[250][250],maxn=-1;
int max(int p,int q) {
return p>q?p:q;
}
int main() {
scanf("%d%d%d",&n,&p,&r);
for(int i=1; i<=n; i++)
scanf("%d%d%d%d",&a[i].vp,&a[i].vr,&a[i].num,&a[i].val);
for(int i=1; i<=n; i++) {
if(a[i].num==0) {
for(int l=1; l<=206; l++)
for(int j=p; j>=a[i].vp; j--)
for(int k=r; k>=a[i].vr; k--)
dp[j][k]=max(dp[j][k],dp[j-a[i].vp][k-a[i].vr]+a[i].val);
} else {
for(int l=1; l<=a[i].num; l++)
for(int j=p; j>=a[i].vp; j--)
for(int k=r; k>=a[i].vr; k--)
dp[j][k]=max(dp[j][k],dp[j-a[i].vp][k-a[i].vr]+a[i].val);
}
}
printf("%d",dp[p][r]);
return 0;
}