数据的储存
目录
-
数据类型详细介绍
-
整型在内存中的存储:原码,反码,补码
-
浮点型在内存中的存储解析
数据类型的详细介绍
char //字符数据类型
short //短整型
int //整型
long //长整型
long long //更长的整型
float //单精度浮点数
double //双精度浮点数
以上就是C语言基本的内置类型,我们可以分为两类,分别是整型和浮点数。
当然还有以下的类型,简单举例:
构造类型:
int arr[100],char arr1[100]//数组类型
struct tag//结构体类型
{
member-list;
}variable-list;
enum a//枚举类型
{
member-list;
}
union //联合体
指针类型
int *a; //整型指针
char *b; //字符指针
float *c;//浮点型指针
void *d; //空指针
空类型:
void //表示空类型
整型在内存中的储存
我们都知道,创建变量需要为变量在内存中开辟空间,空间的大小取决于变量的类型,这样说可能有的抽象,开辟空间,如何把数据储存进去呢?其实储存整型数据,存的是其补码。
我们可以编一个小程序来看看整型的储存:
#include<stdio.h>
int main()
{
int a=10;
int b=-20;
return 0;
}
这是变量a在内存的储存
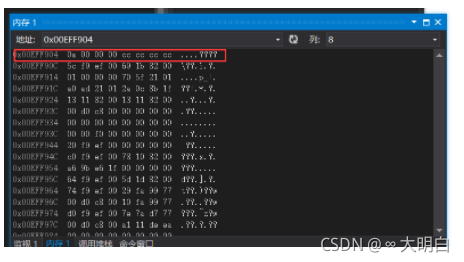
这个 0a就是十六进制的10;二进制是1010。
变量b在内存中的储存:
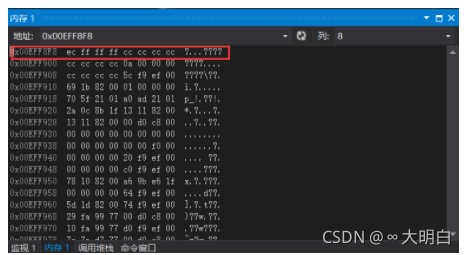
在这里引入大小端字节序,变量a在数据中的存储是0a 00 00 00……,大家有没有想过,它也可以存成00 00 00 ……0a;甚至可以以任意的形式存,这要你可以把数据完整的取出,应用就可以。
所以就延伸出来了大端和小端。
大端存储模式,是指数据的低位保存在内存的高地址处,数据的高位,保存在低地址处。
小端存储模式,是指数据的高位保存在内存的低地址处,数据的高位,保存在高地址处。
从上图,可以判断处这是小端存储,我们也可以编一个小程序来验证。
#include<stdio.h>
int check_sys()
{
int i=1;
return (*(char*)&i);
}
int main()
{
int ret=check_sys();
if(ret==1)
{
printf("是小端储存\n");
}
else
printf("是大端储存\n");
return 0;
}

知道了这个,我们就可以继续深入的讲解,整型数据的存储了。
字符整型是一个字节,它只能储存一个字节,8个比特位的内容,所以输入数据时就会发生截断。char类型可以有符号的和无符号的,它的范围也是可以计算的。写一个程序大家猜一下,运行结果:
#include<stdio.h>
int main()
{
char a = -1;
unsigned char b = -1;
printf("a=%d,b=%d", a, b);
}

大家在这里可能就有点疑惑了,无符号或者有符号不都是一样的吗,它要发生截断呀,明明都是11111111,为啥运行结果不一样呢?
问题出在,以%d的形式打印,这里会发生整型提升,有符号和无符号的整型提升是不一样的,有符号直接在符号位前补符号位的0或1,补到32位。无符号位就是在符号位前直接补0,补齐32位。所以char a,发生整型提升就是111111111……,char b,就是000000000……11111111。
其实整型数据的储存就是存其补码,有大小端字节序之分,如果是char类型,只能存后8个比特位,发生整型提升要看是有符号位还是无符号位的。其它就是4个字节以上的了,一般大小的数据都能储存,当然也会有整型提升的存在,但是遇见的少。
浮点型在内存中的存储解析
浮点数有float,double,long double。我们知道,数据在内存中存的01010101序列,浮点数和整型都是这样,它俩有区别吗?我们可以编写一个程序来验证一下:
int main()
{
int n=9;
float *p=(float*)&n;
printf("n的值位:%的值为%d\n",n);
printf("*ploat的值为:%f\n",*p);
*p=9.0;
printf("n的值为:%d\n",n);
printf("*p的值为:%f\n",*p);
return 0;
}
大家可以想一想,运行的结果。
答案如下:
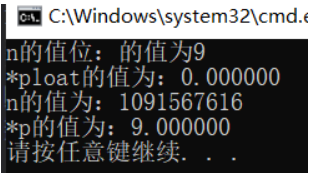
大家在这里可能就产生疑问了?看来浮点数的表示方法和整型不同。
根据国际标准IEEE754,二进制的浮点数可以表示成
(
?
1
)
s
?
M
?
2
E
(-1)^s*M*2^E
(?1)s?M?2E
( ? 1 ) s 表 示 符 号 位 (-1)^s表示符号位 (?1)s表示符号位
M表示有效数字,大于等于1小于2;
2
E
表
示
指
数
位
2^E表示指数位
2E表示指数位
这个类似高中时学的科学计数法,只不过那时学的是十进制,现在学的是二进制,还多了个符号位。
举一个例子:
十进制的5.0,二进制是101.0,相当于1.01*2^2。那么可以知道,s=0,M=1,01,E=2。
现在就说浮点数的储存模型:
- 32位,第一位是s放一个比特位,接下来的8个比特位放E,剩下的都放M。
- 64位,第一位是s放一个比特位,接下来的11个比特位放E,剩下的都放M。
IEEE 754对有效数字M和指数E还有其他的规定。
- 有效数字M因为是大于1的,所以只保存小数点后的有效数字,至于前面的1,会在读取时再加上。
- E因为存在负数的情况,也就是很小的数字,所以规定在储存时加上一个数使其为正数再储存,这得分情况,32位的要加上127进行储存,64位则需要加上1023。
知道了这些,我们再去看看前面的题目。
9的二进制序列为:
0000 0000 0000 0000 0000 0000 0000 1001
可以发现E全为0,因为这是加上127后的结果,所以真实的E=-126,1.001*2^(-126)这样的结果在十进制下是看作0的。
在看可能出现问题的点:
9.0在数据中的存储是:
0 10000010 001 0000 0000 0000 0000 0000
大家可以用计算器换算一下,发现就是运行的结果。
在细说说,9的s=0,M=1.001,E=3+127=130;
前面的第一位是s=0,10000010就是130,紧接着是001,这就是M少了1的数据。
这就是本期内容了!!!
下是看作0的。
在看可能出现问题的点:
9.0在数据中的存储是:
0 10000010 001 0000 0000 0000 0000 0000
大家可以用计算器换算一下,发现就是运行的结果。
在细说说,9的s=0,M=1.001,E=3+127=130;
前面的第一位是s=0,10000010就是130,紧接着是001,这就是M少了1的数据。
这就是本期内容了!!!