题目描述:
题意:
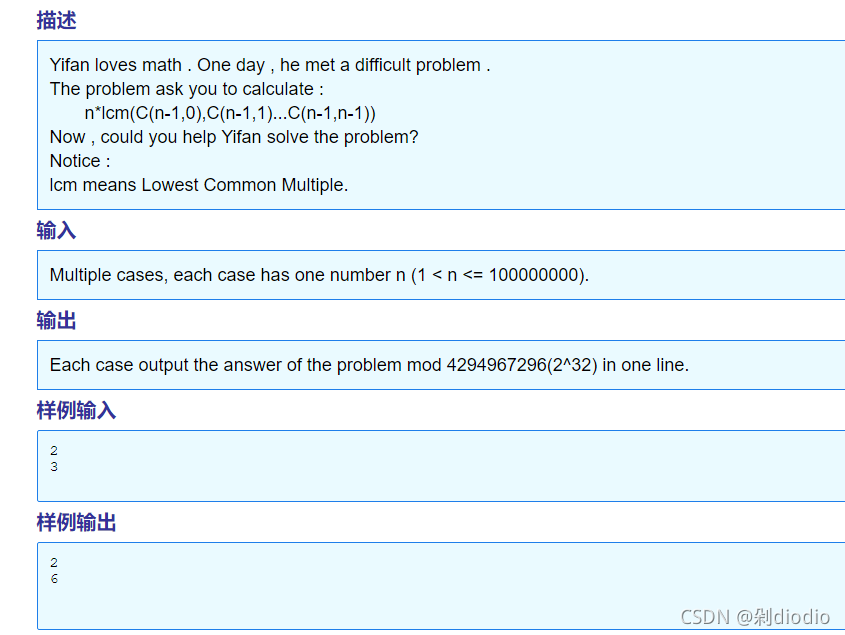
求lcm(1,2,3…n)。
题解:

以上结论其实挺好证明得到。
因为一个数不是一个质数的n次方那么将这个数分解质因数,他的素因子一定包含于前面的lcm。
代码:
因为n的数特别大。普通的欧拉筛素数没法满足,所以就需要用bitset来储存bool数组。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e8+5;
const int M=6e6;
bitset<N>factor;
int prime[M],ans;
unsigned int sum[M];
unsigned int ksm(int a,int n)
{
unsigned int ans=1;
while(n)
{
if(n&1)ans*=a;
a*=a;
n=n>>1;
}
return ans;
}
void init()
{
for(int i=2;i<N;i++)
{
if(!factor[i])
{
prime[++ans]=i;
}
for(int j=1;j<=ans&&i<N/prime[j];j++)
{
factor[i*prime[j]]=1;
if(i%prime[j]==0)
{
break;
}
}
}
sum[1]=2;
for(int i=2;i<=ans;i++)
{
sum[i]=sum[i-1]*prime[i];
}
}
void solve(int n)
{
int pos=upper_bound(prime+1,prime+ans+1,n)-prime-1;
unsigned int ans=sum[pos];
//cout<<pos<<" "<<ans<<endl;
for(int i=1;i<=ans&&prime[i]*prime[i]<=n;i++)
{
int tmp=n,res=0;
while(tmp/prime[i])
{
res++;
tmp/=prime[i];
}
res--;
ans*=ksm(prime[i],res);
}
printf("%u\n",ans);
}
int main()
{
init();
int n;
while(~scanf("%d",&n))
{
solve(n);
}
}