题目链接
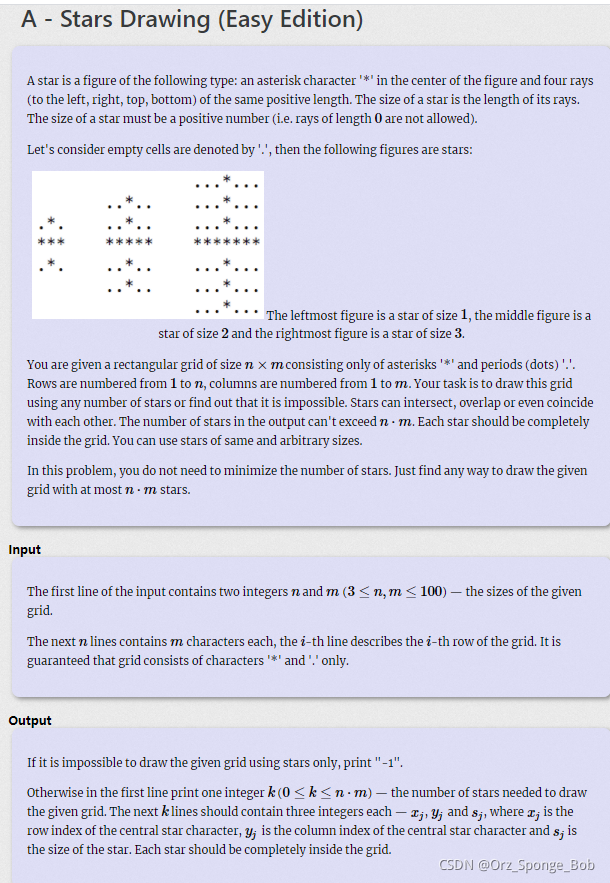
题意:询问能否以 若干个x y作为十字架中心,扩展半径为p 的*十字架 覆盖图中所有的 **
问题分析: emmm暴力
char s[110][110];
ll vis[110][110];
struct pe
{
ll x,y,op;
} a[222222];
ll cnt=0;
signed main()
{
ll n,m;
read(n);
read(m);
for(int i=1; i<=n; i++)
{
scanf("%s",s[i]+1);
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
if(s[i][j]=='*')
{
// i j 中心
ll x1=i;
ll y1=j;
ll x2=i;
ll y2=j;
ll x3=i;
ll y3=j;
ll x4=i;
ll y4=j;
ll len=0;
for(int k=1;; k++)
{
x1--;
x2++;
y3--;
y4++;
if(x1>=1&&x2<=n&&y3>=1&&y4<=m&&s[x1][y1]=='*'&&s[x2][y2]=='*'&&s[x3][y3]=='*'&&s[x4][y4]=='*')
{
len++;
vis[x1][y1]=1;
vis[x2][y2]=1;
vis[x3][y3]=1;
vis[x4][y4]=1;
}
else
{
break;
}
}
if(len==0)
continue;
else
{
vis[i][j]=1;
a[++cnt].x=i;
a[cnt].y=j;
a[cnt].op=len;
}
}
}
}
ll f=0;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
if(s[i][j]=='*'&&vis[i][j]==0)
f=1;
}
}
if(f)
{
printf("-1\n");
return 0;
}
printf("%lld\n",cnt);
for(int i=1; i<=cnt; i++)
{
printf("%lld %lld %lld\n",a[i].x,a[i].y,a[i].op);
}
}

大概意思是2*n个坐标信息,可能是x 或者y 现在我们要重新分配坐标信息,求一个面积最小的矩阵可以覆盖完这n个坐标点 。其实是CSUSTOJ的一道原题吧。
只需要先sort 因为极值是矩阵的len 没毛病了,然后需要宽,就枚举就行了
ll a[222222];
signed main()
{
ll n;
read(n);
for(int i=1; i<=n*2; i++)
{
read(a[i]);
}
sort(a+1,a+1+2*n);
if(n==1)
{
printf("0\n");
return 0;
}
ll ans=(a[n]-a[1])*(a[2*n]-a[n+1]);
ll len=a[2*n]-a[1];
for(int i = 1; i <= n; i++)
{
ans = min(ans, len*(a[i+n-1]-a[i]));
}
printf("%lld\n",ans);
}

题意:0 分的时候开灯,然后后面一次在ai 的时刻关灯,开灯 – 第M分钟全部关闭。现在我们可以至多增加一个新的ai 到该序列的任意位置,询问灯亮的最长时间。
问题分析:其实放在哪里很好考虑,然后就枚举,利用亮灯前缀和/ 关灯前缀和 搞一搞, 有点恶心
ll a[111111];
ll sum[111111];
ll suf[111111];
ll c[111111];
signed main()
{
ll n;
ll m;
read(n);
read(m);
for(int i=1; i<=n; i++)
{
read(a[i]);
}
for(int i=0; i<=n; i++)
{
if(i==0)
{
c[i]=a[1];
continue;
}
if(i==n)
{
c[i]=m-a[n];
continue;
}
c[i]=a[i+1]-a[i];
}
sum[0]=c[0];
sum[1]=c[0];
suf[0]=0;
suf[1]=c[1];
for(int i=2; i<=n; i++)
{
if(i%2==1)
{
sum[i]=sum[i-1];
suf[i]=suf[i-1]+c[i];
}
else
{
suf[i]=suf[i-1];
sum[i]=c[i]+sum[i-1];
}
}
ll ans=0;
for(int i=0; i<=n; ++i)
{
if(i==0)
{
ans=max(ans,sum[n]);
if(a[i]<=1)
continue;
ans=max(ans,suf[n]+a[i]-1);
}
else if(i==n)
{
if(m-a[i]<=1)
continue;
if(i%2==1)
{
ans=max(ans,sum[n-1]+m-a[i]-1);
}
}
if(i%2==1)
{
if(a[i+1]-a[i]<=1)
continue;
ans=max(ans,sum[i-1]+(suf[n]-suf[i])+a[i+1]-a[i]-1);
}
else
{
if(a[i+1]-a[i]<=1)
continue;
}
}
printf("%lld\n",ans );
}
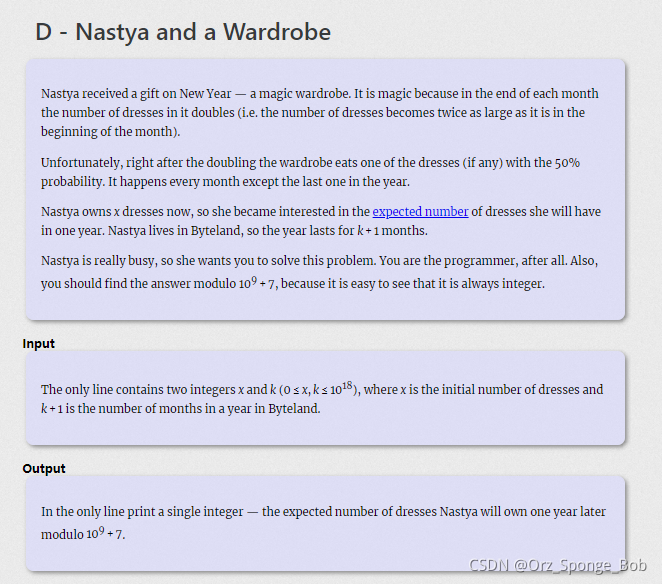
初始衣服每次翻倍,每次50%概率会减少一件,但是第k+1次不会,求最终衣服的期望数量%mod
直接考虑反面去做
signed main(){
ll n,k;
read(n);
read(k);
if(n==0){
printf("0\n");
return 0;
}
n=n%mods;
printf("%lld",(n*qp(2,k+1,mods)%mods-qp(2,k,mods)+1+mods)%mods);
}

对于A B数组 你必须对A数组操作K1次,任选一个数对它+1 或者- 1 同理K2对于B数组。
求最终Σ(ai-bi)2 的最小值
分析:其实 - - k1 k2 可以合并到一起,我们用优先队列处理两个数的绝对值差,显然操作要花在大的数上才是最优的,因此只需要用优先队列每次操作最大值即可,
ll a[222222];
ll b[222222];
priority_queue<ll >q;
signed main(){
ll n,k1,k2;
read(n);
read(k1);
read(k2);
ll op=k1+k2;
for(int i=1;i<=n;i++){
read(a[i]);
}
for(int i=1;i<=n;i++){
read(b[i]);
ll x=abs(a[i]-b[i]);
q.push(x);
}
while(op!=0){
ll now=q.top();
q.pop();
op--;
now--;
now=abs(now);
// printf("??%lld\n",now);
q.push(now);
}
ll ans=0;
while(q.size()){
ll now=q.top();
// printf("Q%lld\n",now);
q.pop();
ans+=now*now;
}
printf("%lld\n",ans);
}