题目链接:
目录
AC篇:
A. Balanced Substring
题意:
给一个由字符‘a’ 与'b'组成的字符串。
找到一段'a'与'b'数目相等的连续子串,输出左右边界。
思路:
数据量很小。o(n^3)直接判断。
题解:
#include <bits/stdc++.h>
#define bbn 200005
#define maxint 2147483647
#define maxLLint 9223372036854775807
#define mod 1000000007 //1e9+7
const double eps=1e-7;
typedef long long int LL;
using namespace std;
int t,n;
bool check(char c[],int x,int y)
{
int q1=0,q2=0;
for(int i=x; i<=y; i++)
{
if(c[i]=='a')
{
q1++;
}
else
{
q2++;
}
}
if(q1==q2)
{
return 1;
}
else
{
return 0;
}
}
int main()
{
cin>>t;
while(t--)
{
cin>>n;
char c[101]= {};
bool judge=0;
cin>>c+1;
for(int i=1; i<=n-1; i++)
{
for(int j=i+1; j<=n; j++)
{
if(check(c,i,j))
{
cout<<i<<" "<<j<<endl;
judge=1;
break;
}
}
if(judge)
{
break;
}
}
if(!judge)
{
cout<<-1<<" "<<-1<<endl;
}
}
}
B. Chess Tournament
题意:
有两种选手比赛。
1表示这个人不能输,2表示这个人赢一把就行。
思路:
1.
人编号相同用 ‘ X ’。
然后四种情况分析。
编号x->编号y :
1->1 :x,y打平局即可。
1->2 :x,y打平局即可。
2->1 :x,y打平局即可。
2->2 :如果x没赢过,让x赢;?如果x赢过,则让y赢。
2.
根据人物种类检查合理性。
横着竖着检查都行,我竖着检查了。
题解:
#include <bits/stdc++.h>
#define bbn 200005
#define maxint 2147483647
#define maxLLint 9223372036854775807
#define mod 1000000007 //1e9+7
const double eps=1e-7;
typedef long long int LL;
using namespace std;
int t,n,a[bbn];
int main()
{
cin>>t;
while(t--)
{
cin>>n;
for(int i=1; i<=n; i++)
{
scanf("%1d",&a[i]);
}
char c[101][101]= {};
bool f[bbn]= {};
for(int i=1; i<=n; i++)
{
for(int j=i; j<=n; j++)
{
if(i==j)
{
c[i][j]='X';
}
else
{
if(a[i]==1||a[j]==1)
{
c[i][j]='=';
c[j][i]='=';
}
else if(a[i]==2&&a[j]==2)
{
if(f[i]==1)
{
c[i][j]='-';
c[j][i]='+';
f[j]=1;
}
else if(!f[i])
{
c[i][j]='+';
c[j][i]='-';
f[i]=1;
}
}
}
}
}//
bool judge=1;
for(int i=1; i<=n; i++)
{
if(a[i]==1)
{
for(int j=1; j<=n; j++)
{
if(c[j][i]=='+')
{
judge=0;
break;
}
}
}
else if(a[i]==2)
{
int sum=0;
for(int j=1; j<=n; j++)
{
if(c[j][i]=='-')
{
sum++;
}
}
if(sum==0)
{
judge=0;
}
}
if(judge==0)
{
break;
}
}//判断是否合理
if(judge==0)
{
cout<<"NO"<<endl;
}
else
{
cout<<"YES"<<endl;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
cout<<c[i][j];
}
cout<<endl;
}
}//输出
}
}
补题篇:
C. Jury Meeting
题意:
n个人讲任务,每人每轮讲一个任务,可以跳过。求合理排列顺序的个数。
合理性 :人不能连续讲任务。
思路:
合理数目=总数目-不合理数目;
不合理数目推导:
n :总人数。max:最大任务数。x:max的数目。k :(max-1)的数目。
两种情况。
x>1时:不合理数目为0。因为这几个轮流来,不会不合理。
x=1时:
max的位置与(max-1)的位置构造的排列数为:
其余任务数的排列数为:
于是不合理排列数为:
题解:
#include <bits/stdc++.h>
#define bbn 200005
#define maxint 2147483647
#define maxLLint 9223372036854775807
#define mod 998244353
const double eps=1e-7;
typedef long long int LL;
using namespace std;
int main()
{
LL t;
cin>>t;
while(t--)
{
LL n,a[bbn]= {};
cin>>n;
for(LL i=1; i<=n; i++)
{
cin>>a[i];
}
LL maxn=0,cnt=0,cntt=0;
maxn=*max_element(a+1,a+n+1);
cnt=count(a+1,a+n+1,maxn);
cntt=count(a+1,a+n+1,maxn-1);
LL ans=1,sub=1;
for(LL i=1; i<=n; i++)
{
ans=ans*i%mod;
if(i!=cntt+1)
{
sub=sub*i%mod;
}
}
if(cnt==1)
{
ans=(ans-sub+mod)%mod;
}
cout<<ans<<endl;
}
}
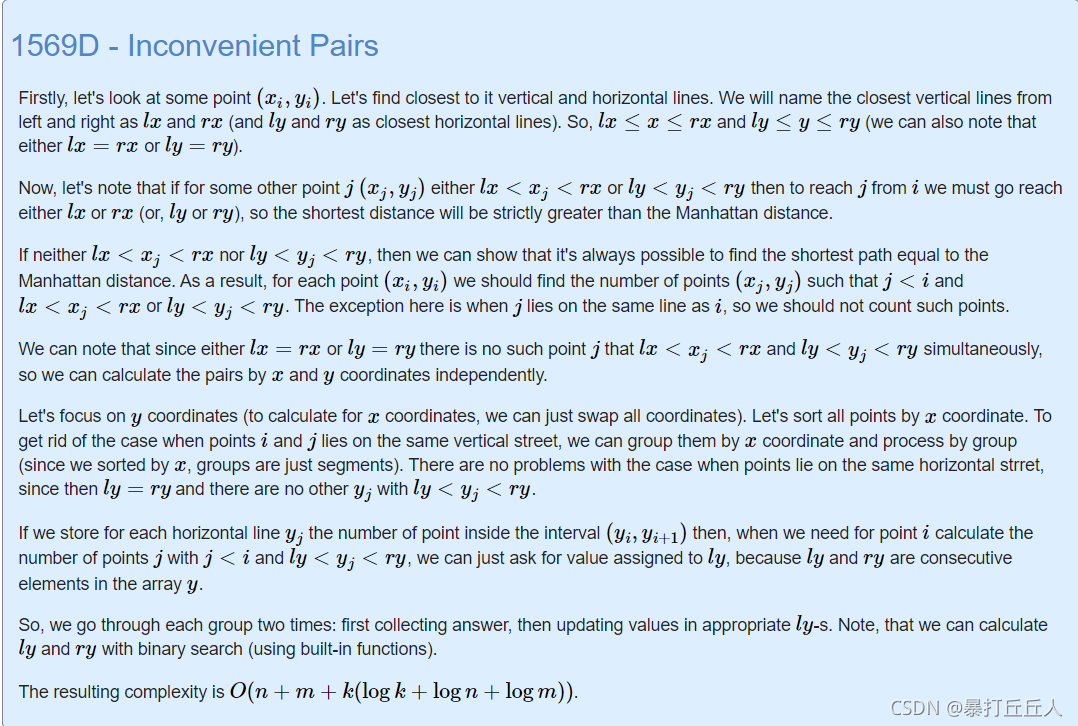
D. Inconvenient Pairs
题意:
给出一些竖线(递增),横线(递增),点(一定在线上)。
求那些 “两点的距离(在线上走的距离)严格大于两点的曼哈顿距离” 的点对数。
思路:
观察数据量,肯定不能o(n^2)
先根据竖轴排列点,对在同一个竖轴上的点分别二分横轴,找到第一个大于等于p.y的横轴,记录,累加。
翻转x,y轴,对称再来一次。
****细节有待思考,太难了。。。救救孩子。。。
英语渣伤不起。。。?
题解:
#include <bits/stdc++.h>
#define bbn 200005
#define maxint 2147483647
#define maxLLint 9223372036854775807
#define mod 1000000007 //1e9+7
const double eps=1e-7;
typedef long long int LL;
using namespace std;
typedef pair<int,int>p;
void solve(int n,int m,int k)
{
vector<int>x(n);
vector<int>y(m);
vector<p>e(k);
for(int i=0; i<n; i++)
{
cin>>x[i];
}
for(int i=0; i<m; i++)
{
cin>>y[i];
}
for(int i=0; i<k; i++)
{
cin>>e[i].first>>e[i].second;
}
LL ans=0;//*
for(int j=1; j<=2; j++)
{
vector<int>cnt(m,0);
sort(e.begin(),e.end());
vector<p>bord(k);
int u=0;
while(u<k)
{
int v=u;
while(v<k&&e[v].first==e[u].first)
{
v++;
}
for(int i=u; i<v; i++)
{
int r=lower_bound(y.begin(),y.end(),e[i].second)-y.begin();
int l=r;
if(y[l]>e[i].second)
{
l--;
}
bord[i]={l,r};
}
for(int i=u; i<v; i++)
{
if(bord[i].first<bord[i].second)
{
ans+=cnt[bord[i].first];
}
}
for(int i=u; i<v; i++)
{
if(bord[i].first<bord[i].second)
{
cnt[bord[i].first]++;
}
}
u=v;
}
for(int i=0; i<k; i++)
{
swap(e[i].first,e[i].second);
}
swap(x,y);
swap(n,m);
}
cout<<ans<<endl;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n,m,k;
cin>>n>>m>>k;
solve(n,m,k);
}
}
总结:
“教育”了。