位运算
位运算是算法题里比较特殊的一种类型,它们利用二进制位运算的特性进行一些奇妙的优化
和计算。常用的位运算符号包括:“∧”按位异或、“&”按位与、“|”按位或、“~”取反、“<<”
算术左移和“>>”算术右移。以下是一些常见的位运算特性,其中 0s 和 1s 分别表示只由 0 或 1
构成的二进制数字。
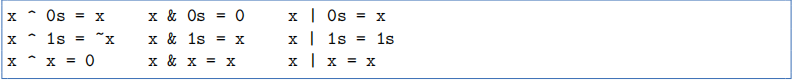
1.基础问题
给定两个十进制数字,求它们二进制表示的汉明距离(Hamming distance,即不同位的个数)。

题解:对两个数进行按位异或操作,统计有多少个1即可。
int hanmingDistance(int x,int y)
{
int diff=x ^ y,ans=0;
while(diff)
{
ans+=diff&1;
diff>>=1;
}
return ans;
}
题目一:
给定一个十进制整数,输出它在二进制下的翻转结果

题解:使用算数左移和右移,可以轻易的实现二进制的翻转
uint32_t reverseBits(unit32_t n)
{
unit32_t ans=0;
for(int i=0;i<32;++i)
{
ans <<= 1;
ans += n & 1;
n >>= 1;
}
return ans;
}
题目二:
给定一个整数数组,这个数组里只有一个数次出现了一次,其余数字出现了两次,求这个只出现一次的数字。

我们可以利用 x ∧ x = 0 和 x ∧ 0 = x 的特点,将数组内所有的数字进行按位异或。出现两次的所有数字按位异或的结果是 0,0 与出现一次的数字异或可以得到这个数字本身。
int singleNumber(vector<int>& nums)
{
int ans=0;
for(const int & num:nums)
{
ans ^= num;
}
return ans;
}
2.二进制特性
利用二进制的一些特性,我们可以把位运算使用到更多问题上。
例如,我们可以利用二进制和位运算输出一个数组的所有子集。假设我们有一个长度为 n 的
数组,我们可以生成长度为 n 的所有二进制,1 表示选取该数字,0 表示不选取。这样我们就获
得了 2n 个子集。
题目一:
给定一个整数,判断它是否是 4 的次方。

首先我们考虑一个数字是不是 2 的(整数)次方:如果一个数字 n 是 2 的整数次方,那么它的二进制一定是 0…010…0 这样的形式;考虑到 n ? 1 的二进制是 0…001…1,这两个数求按位与的结果一定是 0。因此如果 n & (n - 1) 为 0,那么这个数是 2 的次方。如果这个数也是 4 的次方,那二进制表示中 1 的位置必须为奇数位。我们可以把 n 和二进制的 10101…101(即十进制下的 1431655765)做按位与,如果结果不为 0,那么说明这个数是 4 的次方。
bool isPowerOfFour(int n)
{
return n > 0 && !(n & (n-1)) && (n & 1431655765);
}
题目二:
给定多个字母串,求其中任意两个字母串的长度乘积的最大值,且这两个字母串不能含有相同字母。

怎样快速判断两个字母串是否含有重复数字呢?可以为每个字母串建立一个长度为 26 的二进制数字,
每个位置表示是否存在该字母。如果两个字母串含有重复数字,那它们的二进制表示的按位与不为 0。同时,我们可以建立一个哈希表来存储字母串(在数组的位置)到二进制数字的映射关系,方便查找
调用。
int maxProduct(vector<string>& words)
{
unordered_map<int,int>hash;
int ans=0;
for(const string & word : words)
{
int mask=0,size=word.size();
for(const char & c : word)
{
mask |= 1 << (c - 'a');
}
hash[mask] = max(hash[mask],size);
for(const auto& [h_mask,h_len]:hash)
{
if(!(mask & h_mask))
{
ans = max(ans,size * h_len);
}
}
}
return ans;
}
题目三:
给定一个非负整数 n,求从 0 到 n 的所有数字的二进制表达中,分别有多少个 1。
输入是一个非负整数 n,输出是长度为 n + 1 的非负整数数组,每个位置 m 表示 m 的二进制里有多少个 1。

本题可以利用动态规划和位运算进行快速的求解。定义一个数组 dp,其中 dp[i] 表示数字 i的二进制含有 1 的个数。对于第 i 个数字,如果它二进制的最后一位为 1,那么它含有 1 的个数则为 dp[i-1] + 1;如果它二进制的最后一位为 0,那么它含有 1 的个数和其算术右移结果相同,即dp[i>>1]。
vector<int>countBits(int num)
{
vector<int>dp(num+1,0);
for(int i=1;i<=num;++i)
{
dp[i] = i & 1 ? dp[i-1] + 1: dp[i>>1];
//等价于dp[i] = dp[i&(i-1)] + 1;
}
return dp;
}