[C++知识库]爬楼梯(Java/C/C++)

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。
示例 1：

输入： 2 输出： 2 解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入： 3 输出： 3 解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

这个问题是典型的动态规划问题。第n个台阶只能从第n-1或者n-2个上来。到第n-1个台阶的走法 + 第n-2个台阶的走法 = 到第n个台阶的走法，已经知道了第1个和第2个台阶的走法，一路加上去。

f(x)=f(x?1)+f(x?2)

c++

class Solution {
public:
    int climbStairs(int n) {
        if(n == 1){return 1;}
        if(n == 2){return 2;}
        int a = 1, b = 2, temp;
        for(int i =3; i <= n; i++){
            temp = a;
            a = b;
            b = temp + b;
        }
        return b;
    }
};

java

此程序和上面的C++程序大致思路一样，不同的是它的循环是从第一步开始的。

class Solution {
    public int climbStairs(int n) {
        if(n < 3){
            return n;
        }
        int p = 0, q = 0 , r = 1;
        for(int i = 1; i <= n; i++){
            p = q;
            q = r;
            r = p + q;
        }
        return r;
    }
}

C语言

之前的方法我们已经讨论了 f(n)f(n) 是齐次线性递推，根据递推方程 f(n) = f(n - 1) + f(n - 2)f(n)=f(n?1)+f(n?2)，我们可以写出这样的特征方程：

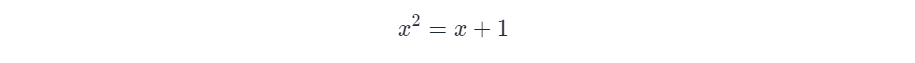
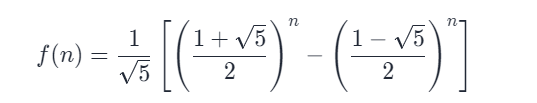
int climbStairs(int n){
     double sqrt5 = sqrt(5);
    double fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1);
    return (int) round(fibn / sqrt5);
}