比赛链接
官方题解链接
1561A Simply Strange Sort 题目链接:点击这里传送

题意:
现给出一串序列,要将其变成升序。关于一趟排序的定义是
for (int i = 1; i <= n-2; i += 2)
{
if (a[i] > a[i + 1]) swap(a[i], a[i + 1]);
}
或者
for (int i = 2; i <= n-1 ; i += 2)
{
if (a[i] > a[i + 1]) swap(a[i], a[i + 1]);
}
问最少要几趟。
思路:
题目咋说就咋做
#include<bits/stdc++.h>
using namespace std;
#define MAXN 1005
int a[MAXN];
int n, t;
bool check()
{
for (int i = 1; i <= n; i++)
{
if (a[i] != i) return 0;
}
return 1;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while (t--)
{
memset(a, 0, sizeof(a));
cin >> n;
int cnt = 0;
for (int i = 1; i <= n; i++) cin >> a[i];
while (1)
{
if (check() == 1) break;
for (int i = 1; i <= n-2; i += 2)
{
if (a[i] > a[i + 1]) swap(a[i], a[i + 1]);
}
cnt++;
if (check()==1) break;
for (int i = 2; i <= n-1 ; i += 2)
{
if (a[i] > a[i + 1]) swap(a[i], a[i + 1]);
}
cnt++;
}
cout << cnt << endl;
}
return 0;
}
1561B Charmed by the Game 题目链接:点击这里传送

题意:
给出一场乒乓球比赛的最终得分,求出所有可能的破发球情况。
思路:
第一视角解说
破发球次数=我方破发球次数+我方被破发球次数
总得分为偶数,我方发球次数=sum
÷
\div
÷ 2
总得分为奇数,我方发球次数=sum
÷
\div
÷ 2或者sum
÷
\div
÷ 2+1。
我方破发球次数=我方得分-我方成功发球次数
我方被破发球次数=我方发球次数-成功发球次数
我方得分已知,我方发球次数已知,只需枚举我方成功发球次数即可。
需要注意的是,我方得是得分少的那个,这样才能确保成功发球次数。如果用得分多的,假设他的分数超过了我方发球次数,那么就不能通过
[
0
,
我
方
得
分
]
\left[0,我方得分\right]
[0,我方得分]来枚举我方发球成功次数了。
#include<bits/stdc++.h>
using namespace std;
set <int> s;
int n, m,t;
int sum;
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while (t--)
{
s.clear();
cin >> n >> m;
sum = n + m;
if (n > m) swap(n, m);
//破发球次数=我方破发球次数+我方被破发次数
//我方破发球次数=我方分数-发球成功次数 n-i
//我方被破发次数=发球总数-成功发球次数 sum/2-i或sum/2+1-i
//发球次数 偶数 sum/2 奇数sum/2+1或sum/2 枚举发球成功次数
if (sum % 2 == 0)
{
for (int i = 0; i <= n; i++) s.insert(n - i + sum / 2 - i);
}
else
{
for (int i = 0; i <= n; i++)
{
s.insert(n - i + sum / 2 - i);
s.insert(n - i + sum / 2 + 1 - i);
}
}
cout << s.size() << endl;
for (auto x : s) cout << x << " ";
cout << endl;
}
return 0;
}
1561C Deep Down Below 题目链接:点击这里传送
题意:
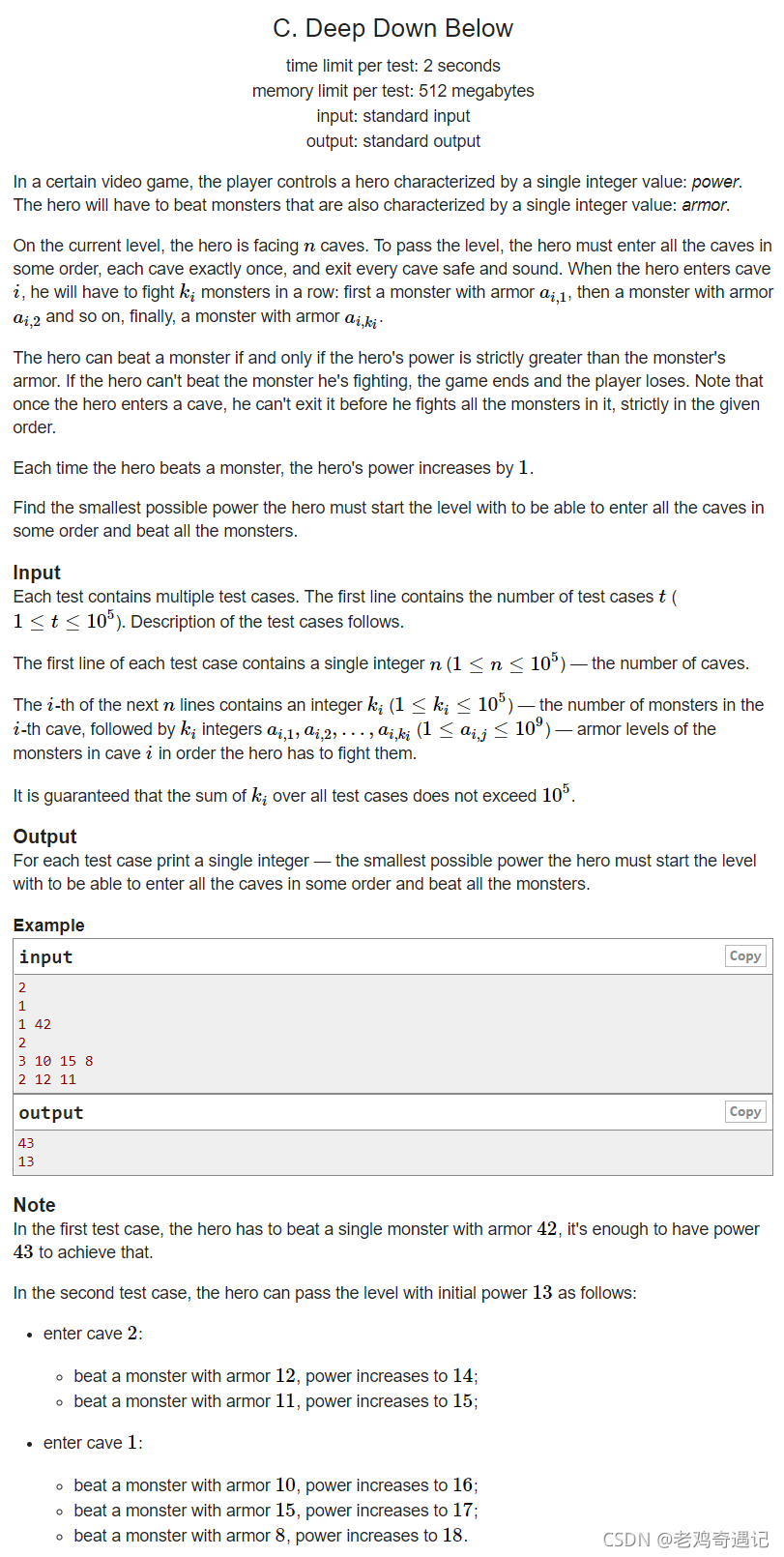
你是一名战士,你要去打怪升级。你有初始攻击力为n点,假设怪物有m点护甲值,只有当n>m时才能打得过怪并且获得+1攻击力,否则你就死了。现在你要去刷副本,一个副本内必须按照给定的怪物顺序一个一个杀过去。你可以任意挑选挑战副本的顺序。现在你有一个修改器,可以调整初始攻击力,问最少需要多少初始攻击力才能打通所有副本。
思路:
设一个副本内怪物的攻击力为
a
i
a_i
ai?,需要
a
1
+
1
a_{1}+1
a1?+1,
a
2
+
1
?
1
a_{2}+1-1
a2?+1?1,
a
3
+
1
?
2
a_3+1-2
a3?+1?2+……+
a
n
+
1
?
(
n
?
1
)
a_n+1-(n-1)
an?+1?(n?1)点攻击力。把这其中最高的攻击力拿出来就是通关这个副本需要的最小攻击力,设他为
b
i
b_i
bi?。
将b数组进行升序排序。进行模拟找出通关所有副本的最小初始攻击力。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int t, n,m;
#define MAXN 100005
ll a[MAXN];//临时处理数据用
struct node
{
ll val;//打通副本需要的最小初始攻击力
int num;
}b[MAXN];
bool cmp(node a, node b) { return a.val < b.val; }
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while (t--)
{
cin >> n;
for (int k = 1; k <= n; k++)//初始攻击力要尽可能小
{
cin >> m;
ll temp = 0;
for (int i = 1; i <= m; i++)
{
cin >> a[i];
a[i] = a[i] - (i - 1);
temp = max(temp, a[i]+1);
}
//cout << "进这个本需要" << " " << temp << endl;
b[k].val = temp;
b[k].num = m;
}
sort(b + 1, b + 1 + n,cmp);//从易到难给副本难度排序
ll ans = 0;
ll num = 0;
ll current_attack = 0;
for (int i = 1; i <= n; i++)
{
if (current_attack >= b[i].val)
{
current_attack += b[i].num;
//cout << current_attack << ">=" << b[i].val << endl;
}
else//攻击力不够,要更新ans
{
//cout << "需要" << b[i].val << "初始力量,减去" << num << endl;
ans = ans + (b[i].val - current_attack);
current_attack = b[i].val+b[i].num;
}
num += b[i].num;
}
cout << ans << endl;
}
return 0;
}
1561D1 Up the Strip (simplified version) 题目链接:点击这里传送
题意:
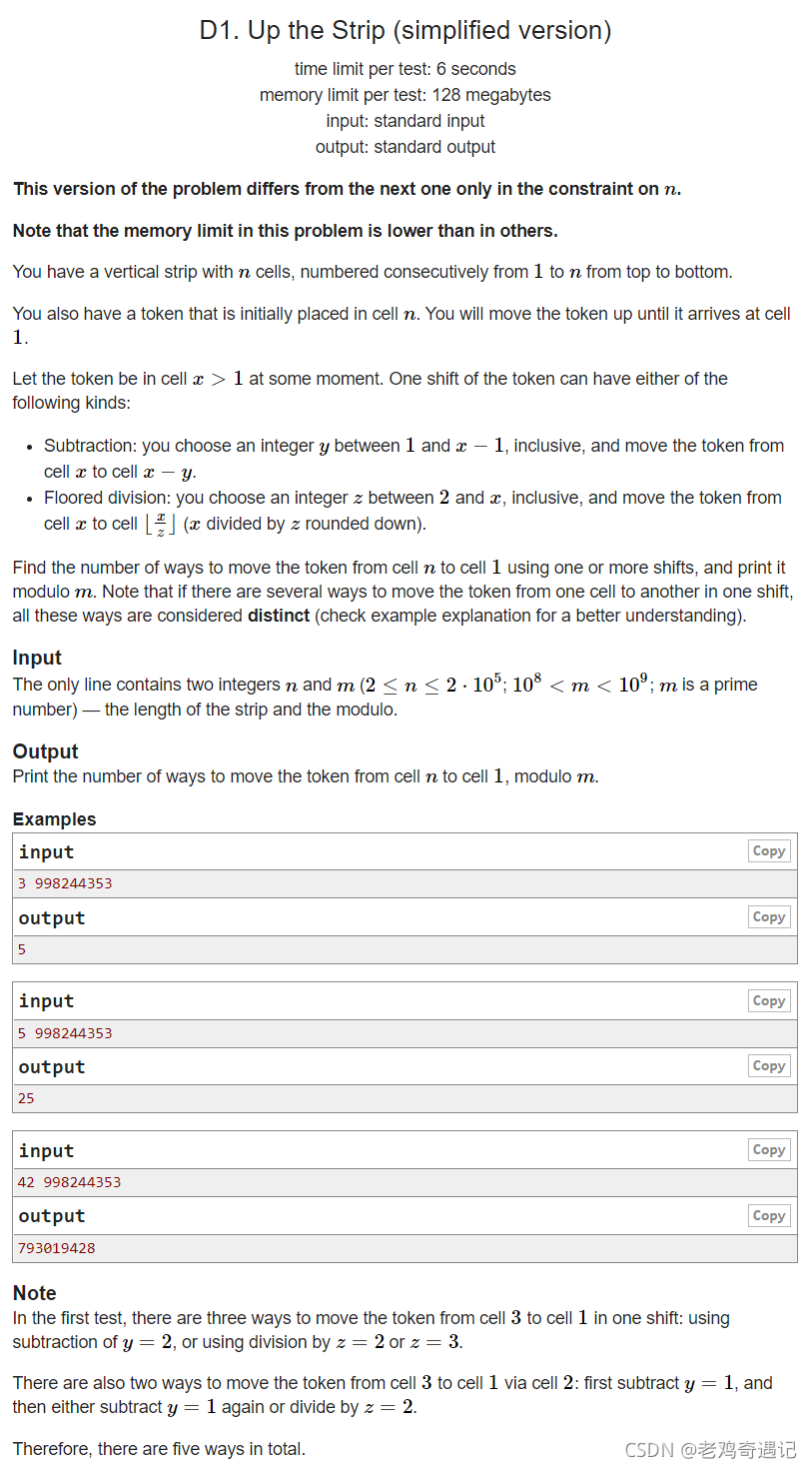
有一个数n,你要将他变成1.你可以把他变成n/2,也可以将他变成n-1,求有多少种操作的方法能将n变为1.
思路:
设dp
[
i
]
\left[i\right]
[i]表示i变为1的方法数。初始化dp
[
1
]
\left[1\right]
[1]=1.
状态转移方程:
d
p
[
i
]
=
d
p
[
i
?
x
]
+
d
p
[
i
/
x
]
dp\left[i\right]=dp\left[i-x\right]+dp\left[i/x\right]
dp[i]=dp[i?x]+dp[i/x],枚举x直接暴力,时间复杂度肯定不够
d
p
[
i
?
x
]
dp\left[i-x\right]
dp[i?x]的和这个式子可以用前缀和表示
∑
x
=
2
i
d
p
[
i
/
x
]
=
d
p
[
i
/
2
]
+
d
p
[
i
/
3
]
+
d
p
[
i
/
4
]
+
…
…
+
d
p
[
i
/
i
]
\sum_{x=2}^i{dp\left[i/x\right]}=dp\left[i/2\right]+dp\left[i/3\right]+dp\left[i/4\right]+……+dp\left[i/i\right]
∑x=2i?dp[i/x]=dp[i/2]+dp[i/3]+dp[i/4]+……+dp[i/i]
d
p
[
i
/
2
]
+
d
p
[
i
/
3
]
+
d
p
[
i
/
4
]
+
…
…
+
d
p
[
i
/
i
]
=
d
p
[
i
/
1
]
+
d
p
[
i
/
2
]
+
d
p
[
i
/
3
]
+
d
p
[
i
/
4
]
+
…
…
+
d
p
[
i
/
i
]
?
d
p
[
i
/
1
]
dp\left[i/2\right]+dp\left[i/3\right]+dp\left[i/4\right]+……+dp\left[i/i\right]=dp\left[i/1\right]+dp\left[i/2\right]+dp\left[i/3\right]+dp\left[i/4\right]+……+dp\left[i/i\right]-dp\left[i/1\right]
dp[i/2]+dp[i/3]+dp[i/4]+……+dp[i/i]=dp[i/1]+dp[i/2]+dp[i/3]+dp[i/4]+……+dp[i/i]?dp[i/1]
这个式子可以用整除分块来做。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define MAXN 200005
ll n, mod;
ll dp[MAXN];//表示i到1有几种方法
ll sum[MAXN];//dp数组的前缀和
//dp[i]=dp[i-1]+dp[i/2]
//可以减去x,可以除以x
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> n >> mod;
dp[1] = 1;
sum[1] = dp[1];
for (int i = 2; i <= n; i++)
{
dp[i] = (dp[i] + sum[i - 1]) % mod;
//dp[i/2]+dp[i/3]+...+dp[i/i]=dp[i/1]+dp[i/2]+dp[i/3]+...+dp[i/i]-dp[i/1]
ll substract = dp[i];
ll ans = 0;
for (int l = 1, r; l <= i; l = r + 1)//整除分块
{
r = i / (i / l);
ans += ((r - l + 1) * (dp[(i / l)%mod])%mod);
}
dp[i] =(dp[i]+ ans - substract)%mod;
sum[i] = (sum[i - 1] + dp[i]) % mod;
}
cout << dp[n];
return 0;
}
D2普通的整除分块也不行,得把 O ( s q r t n ) O(sqrtn) O(sqrtn)的复杂度降到 O ( l o g n ) O(logn) O(logn),不会。