[C++知识库]Educational Codeforces Round 114 (Rated for Div. 2) (A~D) 题解

写完题后胡思乱想了整个晚上，早上眼睛没合写出来的文章，可能有很多错误请谅解，写完就赶着睡觉去了

比赛链接：点击这里传送

1574A Regular Bracket Sequences 题目链接：点击这里传送

题意：
输入一个数n，输出n个不同的由n个左括号和n个右括号组成的合法括号序列
思路：
观察给的数n和下面给出的一组变换。
$最开始为((()))$
$((()))经过了swap(a_3,a_5)变成了(())()$
$(())()经过了swap(a_2,a_4)变成了()()()$
非常有戏剧性的是经过了n-1次变换，(((……)))最终变成了()()()……()()，且中间的括号序列全都合法。就完成了本题的构造。

#include<bits/stdc++.h>
using namespace std;
int t, n;
bool check(string s)
{
	int l = 0;
	int r = 0;
	for (int i = 0; i < s.length(); i++)
	{
		if (s[i] == '(') l++;
		else r++;
		if (r > l) return false;
	}
	if (l != r) return false;
	return true;
}
int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin >> t;
	while (t--)
	{
		cin >> n;
		string s = "";
		for (int i = 1; i <= n; i++) s += "(";
		for (int i = 1; i <= n; i++) s += ')';
		cout << s << endl;
		int m = 1;
		int l = n - 1;
		int r = 2 * n - 2;
		for (int i = 1; i < n; i++)
		{
			swap(s[l], s[r]);
			l--;
			r -= 2;
			cout << s << endl;
		}
	}

	return 0;
}

1574B Combinatorics Homework 题目链接：点击这里传送

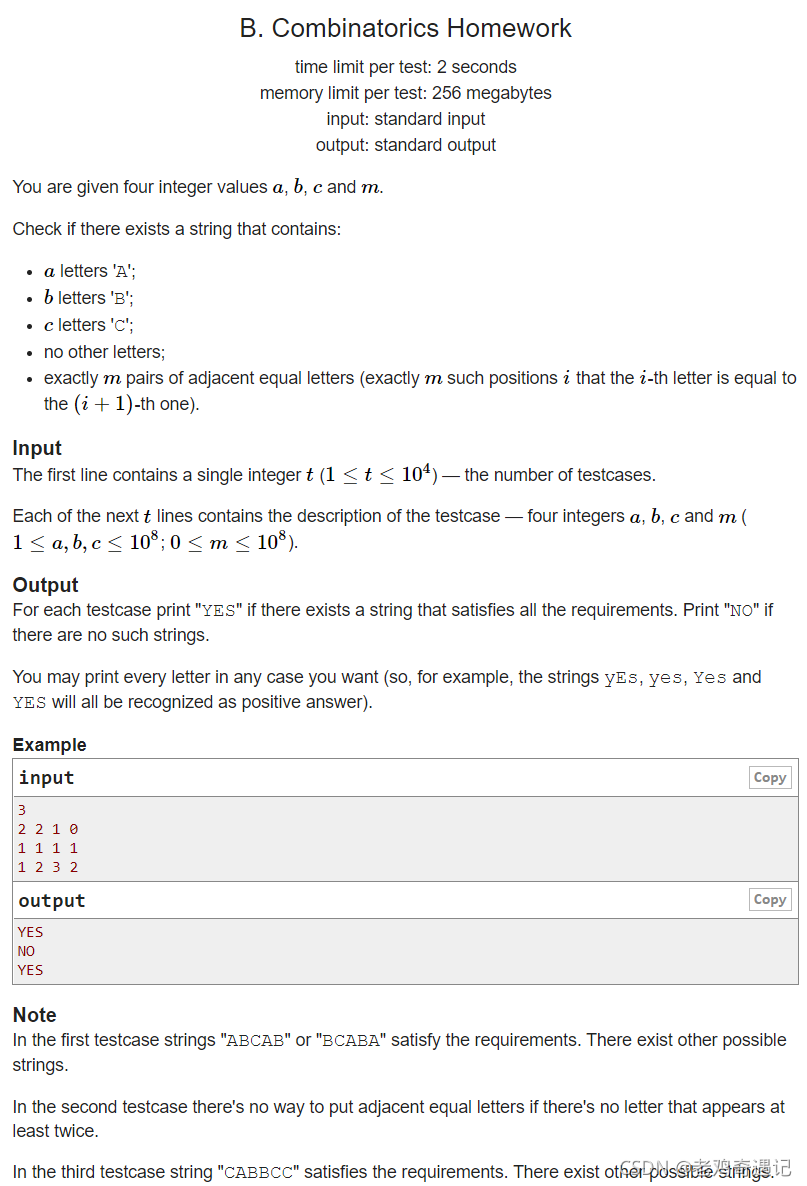
题意：
给出A字符的数量a，B字符的数量b，C字符的数量C，用这些字符组成一个序列。如果序列中存在$a_i=a_{i+1}$的情况，记为贡献+1.现要求这个贡献值为m，能否有一种排列满足这个条件。
思路：
最多能产生$a+b+c?3$个贡献，最少产生的贡献为$max?min?mid?1$，m在这个范围区间内就行。

#include<bits/stdc++.h>
using namespace std;
int t, a, b, c, m;

int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin >> t;
	while (t--)
	{
		cin >> a >> b >> c >> m;
		
		int maxm = max(a, max(b, c));
		int sum = 0;
		sum = a + b + c - maxm;
		if (m <= a + b + c - 3 && m >= maxm - sum - 1) cout << "YES" << endl;//最多产生的括号
		else cout << "NO" << endl;
	}
	return 0;
}

1574C Slay the Dragon 题目链接：点击这里传送

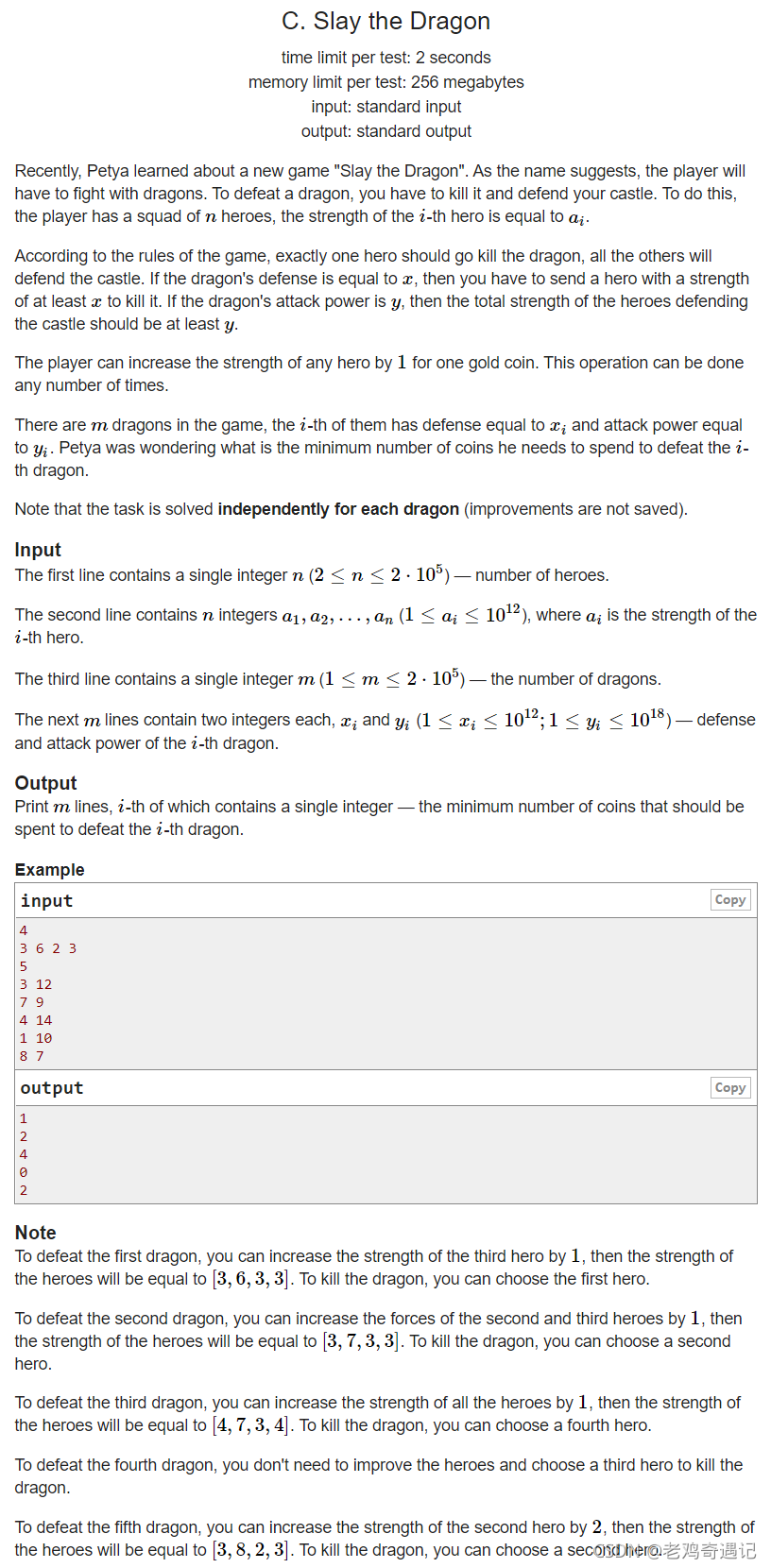
题意：
一共有n个英雄，他们要去屠龙，他们有力量值。一共有m条龙，他有攻击力和防御力，当英雄们决定去杀这条龙时，只能派一人去屠龙，剩下的要守城。屠龙者的力量值要大于等于龙的防御力，剩下守城的人的力量值之和要大于等于龙的攻击力。通过1金币可以增加任意英雄的1点力量值。现求最少需要多少金币，才能杀某条龙（每次屠龙都是独立的过程，之前加的力量值不会累加到下一次屠龙）。
思路：
运用lower_bound函数二分查找第一个力量值大于等于龙的防御力的英雄。

• 如果不存在这个人，也就是龙的甲太高了，直接派最后一个人氪金和他干，剩下的人看情况要不要氪金买甲。
• 如果这个人存在且至少存在一个人杀不动龙。那么就派他去屠龙，剩下的人去守城，但这样可能浪费很多屠龙者的力量值。因此我们再假设一种情况，让比他弱小一点点刚好杀不动龙的人去氪金屠龙，他留下来守城。比较这两种情况所需的金币数量。
• 如果所有人都能屠龙，就让最弱的人去，也不好存在可能浪费很多力量值的情况了，因为只可能浪费更多。

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200005
#define ll long long
ll t;
ll n,m;
ll a[MAXN];
ll power[MAXN];//龙的抛瓦
ll arm[MAXN];//龙的护甲
ll all;
int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
		all += a[i];
	}
	sort(a + 1, a + 1 + n);
	cin >> m;
	for (int i = 1; i <= m; i++)
	{
		cin >> arm[i] >> power[i];
	}
	for (int i = 1; i <= m; i++)//杀第i条龙，剩余m-1条龙进攻
	{
		ll x = arm[i];
		ll y = power[i];
		ll pos = lower_bound(a + 1, a + 1 + n, arm[i]) - a;
		if (arm[i]>a[n])//未能击穿敌方护甲
		{
			cout << (arm[i]-a[n])+max((ll)0,(y-all+a[n])) << endl;
		}
		else
		{
			ll temp = pos - 1;
			ll cost1 = max((ll)0, y - all + a[pos]);
			//cout << "power: " << y << " all: " << all << " a[pos]: " << a[pos] <<" pos: "<<pos <<endl;
			ll cost2;
			//cout << "cost1: " << cost1 << endl;
			if (temp <= 0) cost2 = cost1 + 1;
			else
			{
				cost2 = (arm[i] - a[temp]) + max((ll)0, y - all + a[temp]);
			}
			
			//cout << "cost2: " << cost2 << endl;
			cout << min(cost1, cost2) << endl;
		}
	}
	return 0;
}

1574D The Strongest Build 题目链接：点击这里传送

题意：
给出n个有k个元素的递增序列，有m个限制条件表示为$a_{i1,j1},a_{i2,j2},a_{i3,j3}\dots \dots a_{in,jn}$不能同时出现。现要求每行选一个元素，使得他们的和最大，求出这个最大值。
思路：
事先说明这可能是歪解。
先用哈希把每个限制条件都放到map去。然后遍历限制条件，每次使某个限制元素向左移一位，因为是递增的，所以肯定比限制条件来的小。看能否组成合法条件。如果可以，和当前的最大值进行比较。注意特判所有元素都是最大的情况。

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200005
#define rep(i,x,y) for(int i=x;i<=y;i++)
#define dec(i,x,y) for(int i=x;i>=y;i--)
#define mod 1000001351
#define ll long long
int n, k, x, m;
int maxm , sum;
vector<int>v[15], b[MAXN];//v是原数据，b用来放m的数据也就是限制条件
vector<int>ans, cur;//cur用于后面的处理,哈希函数都以cur为媒介
map<ll, int>mp;//放哈希
ll hashed()//一方面用来生成key值，一方面直接计算当前这n个数的sum值总和
{
    ll temp = 0;
    sum = 0;
    for (int i = 0; i < cur.size(); i++)
    {
        sum += v[i + 1][cur[i] - 1];//原数组中的元素，求和部分
        temp *= 2233;
        temp += cur[i];
        temp %= mod;
    }
    return temp;
}
int main()
{
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n;
    for(int i=1;i<=n;i++)
    {
        cin >> k;
        for(int j=1;j<=k;j++)
        {
            cin >> x;
            v[i].push_back(x);
        }
    }
    cin >> m;
    for(int i=1;i<=m;i++)//给每个限制条件生成哈希
    {
        cur.clear();
        for(int j=1;j<=n;j++)
        {
            cin >> x;
            b[i].push_back(x);
        }
        cur = b[i];
        mp[hashed()] = 1;
    }
    cur.clear();
    for (int i = 1; i <= n;i++)
        cur.push_back(v[i].size());//把最大的数放进去
    if (mp[hashed()]==0)//最大的数满足题意，直接输出
    {
        for (auto it : cur)cout << it << " ";
        return 0;
    }
    for(int i=1;i<=m;i++)//遍历这些限制条件
    {
        for(int j=1;j<=n;j++)
        {
            cur.clear();
            cur = b[i];//下面开始尝试每位遍历减一，因为是递增序列可以贪心 如果能更新就更不能就拉倒 总有一种情况是能更新的 最多1e5个限制条件，乘个10也就1e6，可能常数有点大，反正肯定能找到
            cur[j - 1] = max(cur[j - 1] - 1, 1);//不存在0，最小为1
            if (!mp[hashed()] && sum > maxm)//如果这个序列不是限制条件且和比maxm大
            {
                maxm = sum;
                ans = cur;//更新
            }
        }
    }
    for (auto it : ans)cout << it << " ";
    return 0;
}