[C++知识库]【C++】CINTA学前作业三：C语言程序包GMP的使用

本作业是一项实践操作。GMP是一种非常著名的多精度算术的Library，本作业包括以下内容：

1、阅读浏览GMP的主页，了解GMP的使用，https://gmplib.org/
2、安装GMP包
3、写一个C/C++程序，调用GMP包中的函数完成以下工作：

a、生成两个随机的大素数p和q，分别有512比特长。
b、把p和q相乘，赋值为n。
c、求比n小且与n互素的整数的个数，记为euler，并输出：p、q、n和euler。

4、提交代码和运行截图。

安装与使用GMP包

传送门：https://blog.csdn.net/shangsongwww/article/details/95623176

代码

最开始是逐个遍历，过了老半天觉着不对劲，查了下得用欧拉函数…
https://zhuanlan.zhihu.com/p/151756874
https://blog.csdn.net/liuzibujian/article/details/81086324
https://blog.csdn.net/qq_34446253/article/details/51839005

(先说结果，跑了一星期没运行完，跑那么久估计都是跑在求质数上了
(因为没用VS2019的调试，代码也没设置什么“进度条”之类的东西(当时想着应该不会那么久所以没去弄)，所以跑了一星期到底运行到什么程度，完全没数

#pragma warning(disable:4146)//屏蔽C4146警告

#include "gmp.h"
#pragma comment(lib,"libgmp-10.lib")
#include<time.h>

class MyTimer {//简易计时器
private:
	clock_t clock_start;
	clock_t clock_stop;
public:
	void Start() { clock_start = clock(); }
	void Stop() { clock_stop = clock(); }
	MyTimer() :clock_start(0), clock_stop(0) {}
public:
	struct Time {
		long day;
		long hour;
		long minute;
		long second;
	};
	Time GetResult(unsigned Switch=0b0111) {//second(1)，minute(2)，hour(4)，day(8)。需要哪几个数据就对应置1
	//例如传入Switch=0B0101(代表仅取”时“和”秒“的单位)，若当前计时器计时4100秒，那返回的Time的结果为：day=0,hour=1,minute=0,second=500
		Time rst;
		rst.second = (clock_stop - clock_start)/1000;
		rst.minute= rst.second / 60;
		rst.hour= rst.minute / 60;
		rst.day= rst.hour / 24;
		if (Switch & 0b1000) {//保留“天”
			rst.hour -= rst.day * 24;
			rst.minute -= rst.day * 24 * 60;
			rst.second -= rst.day * 24 * 60 * 60;
		}
		else
			rst.day = 0;
		if (Switch & 0b0100) {//保留“小时”
			rst.minute -= rst.hour*60;
			rst.second -= rst.hour*60*60;
		}
		else
			rst.hour = 0;
		if (Switch & 0b0010) {//保留“分钟”
			rst.second -= rst.minute * 60;
		}
		else
			rst.minute = 0;
		if ((Switch & 0b0001) == 0)
			rst.second = 0;
		return rst;
	}
};

#include<vector>
class Vector_mpzT {//制作极其简陋的mpz_t数组(能跑就行
private:
	std::vector<mpz_ptr>lst;
public:
	~Vector_mpzT() {
		for (auto p = lst.begin(); p != lst.end(); ++p) {
			mpz_clear(*p);
			delete (*p);
		}
	}
	size_t Size()const {
		return lst.size();
	}
	void PushBack(const mpz_ptr num) {
		lst.push_back(new MP_INT);
		mpz_init(lst.back());
		mpz_set(lst.back(), num);
	}
	mpz_ptr operator[](unsigned pst)const {
		if(pst<lst.size())
			return lst[pst];
		return nullptr;
	}
};

class PrimeNums {//质数列表(单例类)
private:
	static PrimeNums* inst;
private:
	mpz_t curr;//当前计算过的数
	mpz_t border;//使用函数ComputeTo时需要记一个边界值以减少遍历次数
	mpz_t tmp;//存储临时计算得到的值
public:
	Vector_mpzT lst;
private:
	PrimeNums(){
		mpz_init(curr);
		mpz_init(border);
		mpz_init(tmp);
		mpz_set_ui(curr, 2);
		lst.PushBack(curr);
		mpz_add_ui(curr,curr,1);
	}
	~PrimeNums() {
		mpz_clear(curr);
		mpz_clear(border);
		mpz_clear(tmp);
	}
public:
	static PrimeNums* GetInstance() {
		if (PrimeNums::inst == nullptr)
			PrimeNums::inst = new PrimeNums();
		return PrimeNums::inst;
	}
	static void ReleaseInstance() {
		if (PrimeNums::inst)
			delete PrimeNums::inst;
		PrimeNums::inst = nullptr;
	}
public:
	const mpz_ptr Curr() { return curr; }
	const mpz_ptr ComputeNext() {//计算出下一个质数并将其返回
		for (;true; mpz_add_ui(curr, curr, 1)) {
			mpz_sqrt(border, curr);
			bool pushFlag = true;
			for (auto p = 0; p < lst.Size(); ++p) {
				mpz_fdiv_r(tmp, curr, lst[p]);
				if (mpz_cmp_ui(tmp, 0) == 0) {//说明lst[p]整除curr
					pushFlag = false;
					break;
				}
			}
			if (pushFlag) {
				lst.PushBack(curr);
				return curr;
			}
		}
	}
	void ComputeTo(const mpz_t& num) {//计算1~num的质数并存放到lst中（代码重复，懒得修了，反正这函数也8会用的
		for (; mpz_cmp(curr, num) <= 0; mpz_add_ui(curr, curr, 1)) {
			mpz_sqrt(border, curr);
			bool pushFlag=true;
			for (auto p = 0; p < lst.Size(); ++p) {
				mpz_fdiv_r(tmp, curr, lst[p]);
				if (mpz_cmp_ui(tmp, 0) == 0) {//说明lst[p]整除curr
					pushFlag = false;
					break;
				}
			}
			if (pushFlag) 
				lst.PushBack(curr);
		}
	}
};
PrimeNums* PrimeNums::inst = nullptr;


int main() {
	MyTimer MT;
	MT.Start();

	gmp_randstate_t grt;//随机数种子
	gmp_randinit_default(grt);
	gmp_randseed_ui(grt, clock());

	mpz_t p, q, n; //整数类型
	mpz_init(p);//变量初始化
	mpz_init(q);
	mpz_init(n);

	mpz_urandomb(p, grt, 512);//p、q随机取值
	mpz_urandomb(q, grt, 512);

	mpz_mul(n, p, q);//n=p*q

	auto primeNums = PrimeNums::GetInstance();
	struct Pairs {
		Vector_mpzT base;
		std::vector<unsigned>index;
		unsigned size=0;
	};
	auto GetFactor = [&primeNums](mpz_t& num)->Pairs*{//返回的是指针，用完要delete掉
		Pairs* rst=new Pairs;
		mpz_t tmp;
		mpz_t targ;
		mpz_t border;
		mpz_init(tmp);
		mpz_init(targ);
		mpz_init(border);
		mpz_set(targ, num);
		mpz_sqrt(border, targ);
		auto& lst = primeNums->lst;
		bool hasExisted = false;//判断当前值lst[p]是否已经加入到rst中
		for (auto p = 0;mpz_cmp(lst[p],border)<=0;) {
			mpz_fdiv_r(tmp, targ, lst[p]);
			if (mpz_cmp_ui(tmp, 0) == 0) {//说明lst[p]能整除targ
				if (hasExisted)
					++rst->index.back();
				else {
					rst->base.PushBack(lst[p]);
					rst->index.push_back(1);
					++rst->size;
					hasExisted = true;
				}
				mpz_fdiv_q(targ, targ, lst[p]);
			}
			else {
				if(hasExisted)//说明targ更新
					mpz_sqrt(border, targ);//也更新border
				hasExisted = false;
				++p;
				if (p == lst.Size())
					primeNums->ComputeNext();
			}
		}
		if (mpz_cmp_ui(targ, 1) != 0) {
			rst->base.PushBack(targ);
			rst->index.push_back(1);
			++rst->size;
		}
		mpz_clear(tmp);
		mpz_clear(targ);
		mpz_clear(border);
		return rst;
	};
	auto factor_P = GetFactor(p);
	auto factor_Q =GetFactor(q);

	//使用欧拉函数
	mpz_t euler;
	mpz_t tmp;
	mpz_init(euler);
	mpz_init(tmp);
	mpz_set_ui(euler, 1);
	unsigned pst_p = 0;
	unsigned pst_q = 0;
	for(;pst_p<factor_P->size&&pst_q<factor_Q->size;){
		int cmp = mpz_cmp(factor_P->base[pst_p], factor_Q->base[pst_q]);
		if (cmp < 0) {
			gmp_printf("%Zd^%d\n", factor_P->base[pst_p], factor_P->index[pst_p]);
			mpz_pow_ui(tmp, factor_P->base[pst_p], factor_P->index[pst_p]-1);
			mpz_mul(euler, euler, tmp);
			mpz_sub_ui(tmp, factor_P->base[pst_p], 1);
			mpz_mul(euler, euler, tmp);
			++pst_p;
		}
		if (cmp == 0) {
			gmp_printf("%Zd^%d\n", factor_P->base[pst_p], factor_P->index[pst_p]+factor_Q->index[pst_q]);
			mpz_pow_ui(tmp, factor_P->base[pst_p], factor_P->index[pst_p] + factor_Q->index[pst_q] - 1);
			mpz_mul(euler, euler, tmp);
			mpz_sub_ui(tmp, factor_P->base[pst_p], 1);
			mpz_mul(euler, euler, tmp);
			++pst_p;
			++pst_q;
		}
		if (cmp > 0) {
			gmp_printf("%Zd^%d\n", factor_Q->base[pst_q], factor_Q->index[pst_q]);
			mpz_pow_ui(tmp, factor_Q->base[pst_q], factor_Q->index[pst_q] - 1);
			mpz_mul(euler, euler, tmp);
			mpz_sub_ui(tmp, factor_Q->base[pst_q], 1);
			mpz_mul(euler, euler, tmp);
			++pst_q;
		}
	}
	Pairs* factor_rest = pst_p!=factor_P->size?factor_P:pst_q!=factor_Q->size?factor_Q:nullptr;
	unsigned pst_rest = pst_p != factor_P->size ? pst_p : pst_q;
	if (factor_rest) {
		while (pst_rest < factor_rest->size) {
			gmp_printf("%Zd^%d\n", factor_rest->base[pst_rest], factor_rest->index[pst_rest]);
			mpz_pow_ui(tmp, factor_rest->base[pst_rest], factor_rest->index[pst_rest] - 1);
			mpz_mul(euler, euler, tmp);
			mpz_sub_ui(tmp, factor_rest->base[pst_rest], 1);
			mpz_mul(euler, euler, tmp);
			++pst_rest;
		}
	}

	MT.Stop();
	auto time=MT.GetResult();
	printf("\n\n【用时(时分秒)：%d:%d:%d】\n\n",time.hour,time.minute,time.second);
	gmp_printf("【P】0x%ZX\n\n", p);
	gmp_printf("【q】0x%ZX\n\n", q);
	gmp_printf("【n】0x%ZX\n\n", n);
	gmp_printf("【euler】%Zd\n\n", euler);
	system("pause");

	mpz_clear(p);
	mpz_clear(q);
	mpz_clear(n);
	mpz_clear(euler);
	mpz_clear(tmp);
	delete factor_P;
	delete factor_Q;
	PrimeNums::ReleaseInstance();

	return 0;
}

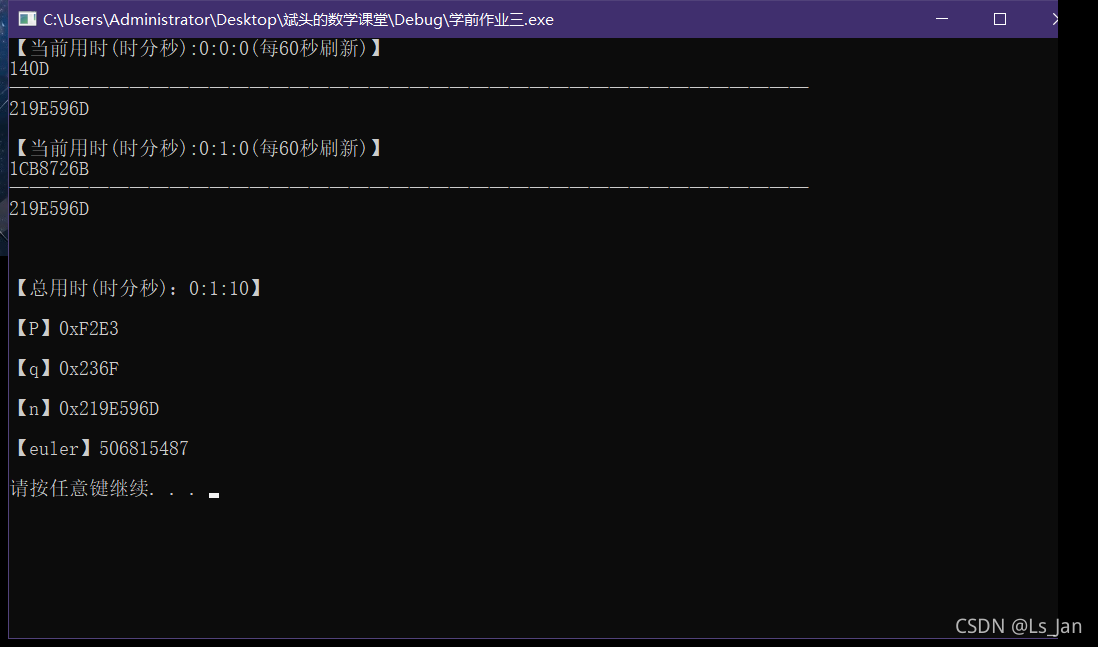
运行结果

下面这个是遍历的，核对上面的运行结果。
求得结果少了1个是因为我这里没把’1’算进里面。