开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> C++知识库 -> 第三章——队列 -> 正文阅读

[C++知识库]第三章——队列

队列的定义

队列简称队，也是一种操作受限的线性表，其限制为仅允许在表的一端进行插入，在表的另一端进行删除操作，把进行插入的一端称为队尾(rear)，向队列插入新元素称为进队或入队(enqueue)，新元素进队之后成为新的队尾元素；从队列删除元素称为出队或离队(dequeue)，元素出队后，其直接后继元素就成为新的队首元素。

由于队列元素进出的规则，队列又称为先进先出(FIFO)表。

需要注意的是，以上的规则仅对普通队列成立，双端队列两端都可以进行插入和删除。

队列的抽象数据类型描述

了解基本运算：

InitQueue(&q):初始化队列,构造一个空队列q
DestroyQueue(&q):销毁队列,释放队列q占用的存储空间
QueueEmpty(q):判断队列是否为空,若队列为空,则返回真,否则返回假 
enQueue(&q,e):进队列,将元素e进队作为队尾元素
deQueue(&q,&e):出队列,从队列q中出队一个元素,并将其值赋给e

和栈一样，事实上还有很多的操作，不过里面比较基本的就是这几个操作。

队列的顺序存储结构

同样对于队列有两种模板，采用顺序存储结构的队列称为顺序队。

struct SqQueue{ElemType data[MaxSize]; int front,rear;};//front和rear分别表示队头和队尾指针

基本运算的实现

顺序存储结构的都不难写。但在编写之前，希望大家每次搞不清front和rear到底指向什么时，就来看看下面的这张图：

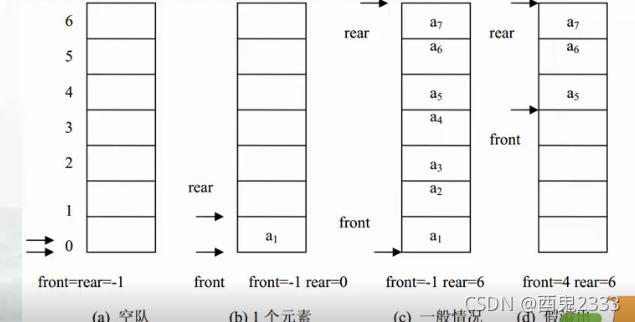
在这里插入图片描述

front指向队首元素的前一个元素，rear指向队尾元素。

初始化队列

和栈一样，将两个指针设置为-1即可。

//初始化队列,将队头和队尾指针全部设置为-1即可 
void InitQueue(SqQueue *&q){q=(SqQueue *)malloc(sizeof(SqQueue)); q->front=q->rear=-1;}

销毁队列

顺序存储结构释放容器占用的空间都是一样的。

//销毁队列 
void DestroyQueue(SqQueue *&q){free(q);}

判断队列是否为空

队列为空时，队首的指针和队尾的指针的指向相同：

//判断队列是否为空
bool QueueEmpty(SqQueue *q){return(q->front==q->rear);}

进队列

在队列不满时，先将队尾指针rear++，然后将元素e插入到该位置：

//进队列 
bool enQueue(SqQueue *&q,ElemType e){if (q->rear==MaxSize-1) return false;//队列q(伪)放满					
	q->rear++;	q->data[q->rear]=e;	return true;						
}

为什么在这里添加一个伪字呢？因为q->rear==MaxSize-1时，队列中往往还存在很多空位置，这种因为队满条件设置不合理导致队满条件成立而队列中仍有空间的情况称为假溢出。后面会介绍另外一种大家熟悉地方式来解决这个问题。

出队列

需要判断一下队列是否为空。

//出队列,队列为空时队列中没有元素,出队失败 
bool deQueue(SqQueue *&q,ElemType &e){if (q->front==q->rear) return false;
	q->front++; e=q->data[q->front]; return true;
}

基本运算合集如下：

struct SqQueue{ElemType data[MaxSize]; int front,rear;};//front和rear分别表示队头和队尾指针
//初始化队列,将队头和队尾指针全部设置为-1即可 
void InitQueue(SqQueue *&q){q=(SqQueue *)malloc(sizeof(SqQueue)); q->front=q->rear=-1;}
//销毁队列 
void DestroyQueue(SqQueue *&q){free(q);}
//判断队列是否为空
bool QueueEmpty(SqQueue *q){return(q->front==q->rear);}
//进队列 
bool enQueue(SqQueue *&q,ElemType e){if (q->rear==MaxSize-1) return false;//队列q(伪)放满					
	q->rear++;	q->data[q->rear]=e;	return true;						
}//出队列,队列为空时队列中没有元素,出队失败 
bool deQueue(SqQueue *&q,ElemType &e){if (q->front==q->rear) return false;
	q->front++; e=q->data[q->front]; return true;
}

环形队列

接下来处理上面提出的假溢出的问题。

其实解决方案也很简单，还记得链表中的循环链表么，我们在队列中使用类似的结构，将队尾的假溢出的元素放入队首之前没有使用的空间即可。

这种数据结构我们称为环形队列，基本运算与队列一致，只是在front和rear++时需要添加一个%MaxSize保证环形结构。

struct SqQueue{ElemType data[MaxSize]; int front,rear;};//front和rear分别表示队头和队尾指针
//初始化队列,将队头和队尾指针全部设置为-1即可 
void InitQueue(SqQueue *&q){q=(SqQueue *)malloc(sizeof(SqQueue)); q->front=q->rear=0;}
//销毁队列 
void DestroyQueue(SqQueue *&q){free(q);}
//判断队列是否为空
bool QueueEmpty(SqQueue *q){return(q->front==q->rear);}
//进队列,环形队列放满的情况即在于队尾元素放置的位置与队首元素放置的位置相邻 
bool enQueue(SqQueue *&q,ElemType e){if ((q->rear+1)%MaxSize==q->front) return false;					
	q->rear=(q->rear+1)%MaxSize; q->data[q->rear]=e; return true;						
}//出队列,队列为空时队列中没有元素,出队失败 
bool deQueue(SqQueue *&q,ElemType &e){if (q->front==q->rear) return false;
	q->front=(q->front+1)%MaxSize; e=q->data[q->front]; return true;
}

例题3.7难度和意义不大，不多作讨论(就是用长度len代替rear和front的差，用len和front描述一个环形队列)。

队列的链式存储结构

采用链式存储结构的队列称为链队，同样用单链表来实现链队。

和链栈不同的是，链栈用头插法的方法建立栈，于是只需要结点的结构体。链队则同时需要两个结构体。

struct DataNode{ElemType data; DataNode *next;};//链队单个结点的结构体类型 
struct LinkQuNode{DataNode *front; DataNode *rear;};//链队

基本运算的实现

首先还是先了解一下链队直观上是如何存在的：

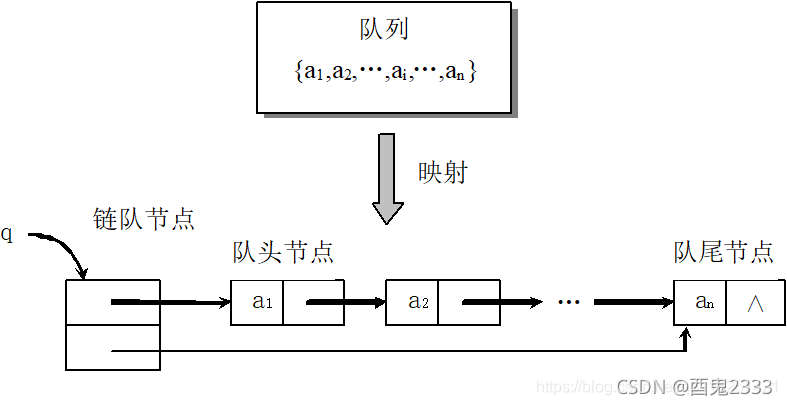
在这里插入图片描述

初始化队列

和顺队列一样，让front和rear指向一个无意义的值即可：

//初始化队列
void InitQueue(LinkQuNode *&q){q=(LinkQuNode *)malloc(sizeof(LinkQuNode)); q->front=q->rear=NULL;}

销毁队列

和链栈一样，一个元素遍历链式结构，另一个元素存储后继结点：

//销毁队列
void DestroyQueue(LinkQuNode *&q){DataNode *p=q->front,*r;//p为当前删除的结点 
	if (p!=NULL){r=p->next;//r存储next域 
		while (r!=NULL) {free(p); p=r; r=p->next;} free(p);//释放最后一个结点 
	}free(q);//释放链队				
}

判断队列是否为空

//判断队列是否为空,尾结点指向的元素没有data域,直接为NULL即为空表 
bool QueueEmpty(LinkQuNode *q){return(q->rear==NULL);}

进队

和链栈不一样，链栈是头插法，而队列中我们知道尾结点的位置，那么直接插入到尾结点之后即可。不过需要判断一下是否为空表，如果为空表，front和rear的指向是相同的：

//进队 
void enQueue(LinkQuNode *&q,ElemType e){DataNode *p; p=(DataNode *)malloc(sizeof(DataNode));
	p->data=e; p->next=NULL;//创建尾结点,进队的元素为新的尾结点 
	if (q->rear==NULL) q->front=q->rear=p;//若链队为空,则新结点是队首结点又是队尾结点
	else {q->rear->next=p; q->rear=p;}//将新节点插入到队尾 
}

出队

这个和链栈区别不大：

//出队 
bool deQueue(LinkQuNode *&q,ElemType &e){DataNode *t;
	if (q->rear==NULL) return false;//如果链队为空,出队失败 
	t=q->front;	e=t->data;			
	if (q->front==q->rear) q->front=q->rear=NULL;//队列中只有一个结点时,出队同时改变front和rear域 
	else q->front=q->front->next;//删除front结点 
	free(t); return true;//释放删除结点的空间 
}

基本操作合集如下：

struct DataNode{ElemType data; DataNode *next;};//链队单个结点的结构体类型 
struct LinkQuNode{DataNode *front; DataNode *rear;};//链队
//初始化队列
void InitQueue(LinkQuNode *&q){q=(LinkQuNode *)malloc(sizeof(LinkQuNode)); q->front=q->rear=NULL;}
//销毁队列
void DestroyQueue(LinkQuNode *&q){DataNode *p=q->front,*r;//p为当前删除的结点 
	if (p!=NULL){r=p->next;//r存储next域 
		while (r!=NULL) {free(p); p=r; r=p->next;} free(p);//释放最后一个结点 
	}free(q);//释放链队				
}//判断队列是否为空,尾结点指向的元素没有data域,直接为NULL即为空表 
bool QueueEmpty(LinkQuNode *q){return(q->rear==NULL);}
//进队 
void enQueue(LinkQuNode *&q,ElemType e){DataNode *p; p=(DataNode *)malloc(sizeof(DataNode));
	p->data=e; p->next=NULL;//创建尾结点,进队的元素为新的尾结点 
	if (q->rear==NULL) q->front=q->rear=p;//若链队为空,则新结点是队首结点又是队尾结点
	else {q->rear->next=p; q->rear=p;}//将新节点插入到队尾 
}//出队 
bool deQueue(LinkQuNode *&q,ElemType &e){DataNode *t;
	if (q->rear==NULL) return false;//如果链队为空,出队失败 
	t=q->front;	e=t->data;			
	if (q->front==q->rear) q->front=q->rear=NULL;//队列中只有一个结点时,出队同时改变front和rear域 
	else q->front=q->front->next;//删除front结点 
	free(t); return true;//释放删除结点的空间 
}

例3.8就是让我们用循环单链表为模板存储队列，由于循环单链表尾结点指向头节点，于是只需一个尾结点即可(为什么不是头结点，因为尾结点可以指向头结点，头结点不能指向尾结点)，于是和链栈一样只需要一个结点的结构体即可：

struct LinkNode{ElemType data; node *next;};
//初始化队列 
void initQueue(LinkNode *&rear){rear=NULL;}
//判断队列是否为空 
bool queueEmpty(LinkNode *rear){return(rear==NULL);}
//进队 
void enQueue(LinkNode *&rear,ElemType e){LinkNode *p; 
	p=(LinkNode *)malloc(sizeof(LinkNode));	p->data=e;
	if (rear==NULL){p->next=p; rear=p;}//如果链队为空,rear设为新节点,rear自己指向自己 
	else{p->next=rear->next; rear->next=p; rear=p;//将新节点插入到p之后,rear修改为p								
	}
}//出队 
bool deQueue(LinkNode *&rear,ElemType &e){LinkNode *q; if (rear==NULL) return false;//空队出队失败
 	//如果链队只有一个元素,即rear指向的元素,直接free(rear)即可
	//因为剩下的链队为空,不需要维持循环的特性 
	else if (rear->next==rear){e=rear->data; free(rear); rear=NULL;}
	//否则需要保存rear的next域即隐去的front,让rear指向原本front的next(不用修改front) 
	else {q=rear->next; e=q->data; rear->next=q->next; free(q);}
	return true;
}

和循环链表与链表的区别是非常类似的，但是循环链表与链表，循环双链表与双链表，特殊节点(头结点和尾结点)的个数是相同的，这里实现的链队比起原本的链队不需要front域。

队列的应用

求解报数问题

设有n个人站成一排，从左到右的编号分别为1-n，现在从左往右报数“1,2,1,2·····”，报1的人出队，数到2的人立刻站到队伍的最右侧。报数反复进行，直到n个人全部出列为止，要求给出他们的出列顺序。

分析：很简单的一个问题啊，队列之所以叫队列，就是因为它和排队的队列非常类似，直接模拟即可：

void number(int n){int e;
	SqQueue *q;	InitQueue(q); for (int i=1;i<=n;i++) enQueue(q,i);//构建初始队列 
	while (!QueueEmpty(q)){deQueue(q,e); printf("%d ",e);//报号为1的人出队 
		if (!QueueEmpty(q))	{deQueue(q,e); enQueue(q,e);}//报号为2的人出队后,进队尾 
	}DestroyQueue(q); //销毁队列q
}

求解迷宫问题

就是栈那里的迷宫问题，这里用队列来解决。

分析：这里就是我上一章节提到的简化后的BFS，对BFS不太了解的可以去看一下我最近刚刚整理的博客：BFS(DFS的整理很快就来，很快！这个礼拜！)

直接看代码吧：

struct Box{int i,j,pre;};//(i,j)表示坐标,pre表示路径中上一方块在队列中的下标
//(xi,yi)表示起点坐标,(xe,ye)表示终点坐标,e和e_即为我们常写的start和next 
bool mgpath1(int xi,int yi,int xe,int ye){Box e,e_; e.i=xi; e.j=yi; e.pre=-1;
	QuType *qu;	InitQueue(qu); enQueue(qu,e); mg[xi][yi]=-1;//mg用于判重,防止一个结点被重复遍历					
	while (!QueueEmpty(qu)){deQueue(qu,e);//BFS的标准格式,出队一个元素判断是否为目标结点			
		if (e.i==xe && e.j==ye){print(qu,qu->front); DestroyQueue(qu); return true;}
		for (int i=0;i<4;i++){//这个switch相当于扫描了当前结点可扩展的四个方位
			switch(di){//不过为了代码简单,一般用方向数组写比较好 
				case 0:e_.i=e.i-1; e_.j=e.j;   break;
				case 1:e_.i=e.i;   e_.j=e.j+1; break;
				case 2:e_.i=e.i+1; e_.j=e.j;   break;
				case 3:e_.i=e.i;   e_.j=e.j-1; break;
			}//判断扩展结点是否可到达(这里缺少了一个判断是否越界) 
			if (mg[e_.i][e_.j]==0){e_.pre=qu->front;//将扩展出来的新节点添加到队列中	
				enQueue(qu,e); mg[i1][j1]=-1;//扩展出来的新节点需要进行标记		
			}
		}
    } DestroyQueue(qu); return false;				
}

就是标准的BFS格式，不过有些细节，比如方向数组判重那里还是不一样，需要注意的是扩展新节点这里光光判重不够还需要判断是否越界。

至于打印路径的方法，我发现是一个用时间换空间的方法，我个人觉得BFS的状态结点(比如状态图问题)会很多，这样子处理的效率往往很低，但还是看一下这个处理方法：

void print(QuType *qu,int front){int p1=front,p2;//用p1向前遍历整个遍历,将整个路径的pre值全部修改为-1 
	do{	p2=p1; p1=qu->data[p1].pre;//p2存储原本p1的值 
		qu->data[p2].pre=-1;//在p1向前遍历之后修改pre的值为-1 
	} while (p1!=0);//这个为什么不是!=-1,我表示疑惑
	//直接从data数组找pre为-1的结点直接打印 
	for (int i=0;i<MaxSize;i++) if (qu->data[k].pre==-1) 
	printf("(%d,%d)\t",qu->data[k].i,qu->data[k].j);
}

整个这个算法的想法·······，只能说建立在手写queue的基础上。因为如果你不是自己手写的queue(这里的queue是非环形队列，为了防止队尾元素加入到队首之前，最后在打印路径时从小到大的遍历出现问题)，用的stl的queue，你是无法访问到出队的元素(我这里看了一下源码出队函数的编写，发现果然没有释放空间，就是直接front++的)。

于是出队之前不用保存上一个结点的信息，同时最后打印路径时，可以直接通过data数组的pre值找到路径。

还是值得细细品味的做法。

双端队列

前面提了一下就是两端，都可以进行进队和出队操作的队列。

其他操作一致，就是多了从队尾删除和从队首插入的基本运算，模板是环形队列。

从队尾删除

其实区别也不大，就是front和rear互换一下。

//从队尾删除
bool deQueue1(SqQueue *&q,ElemType &e){if (q->front==q->rear) return false;//队空删除失败 
	e=q->data[q->rear];	q->rear=(q->rear-1+MaxSize)%MaxSize;//修改队尾指针 
	return true;
}

从队头插入

//从队头插入
bool enQueue1(SqQueue *&q,ElemType e){if ((q->rear+1)%MaxSize==q->front) return false;//满队时插入失败 
	q->data[q->front]=e; q->front=(q->front-1+MaxSize)%MaxSize;//修改队头指针	
	return true;
}