首先,让我们来看一段代码:
C++中
printf("%.2f\n", 9.825f);
printf("%.2f\n", 9.835f);
printf("%.2f\n", 9.845f);
或者Python中
print("%.2f" % 9.825)
print("%.2f" % 9.835)
print("%.2f" % 9.845)
上述这段代码的结果是什么呢?(C++和Python中进位方式处理是一致的,看其中一中就可以了。)
结果是
9.82
9.84
9.85
这是因为采用的是一中叫“四舍六入五成双”的规则。那什么是“四舍六入五成双”呢?其含义如下:
所谓“四舍六入五成双”,即“4舍6入5凑偶”,这里“四”是指≤4 时舍去,"六"是指≥6时进上,"五"指的是根据5后面的数字来定,当5后有数时,舍5入1;当5后无有效数字时,需要分两种情况来讲:
(1)5前为奇数,舍5入1;
(2)5前为偶数,舍5不进(0是偶数)。
例如:
9.8249=9.82, 9.82671=9.83
9.8350=9.84, 9.83501=9.84
9.8250=9.82, 9.82501=9.83
按照这个规则,上面的9.825取舍后就是9.82,9.835取舍后就是9.84,9.845取舍后就是0.84。但是,9.845的结果跟上面不一样,这又是为什么呢?这里需要注意的是,虽然我们看到的是9.825,9.835,9.845这样的数,但是它们在计算机中实际存储时并不是这样的。下面我们来介绍下浮点数在计算机中的存储方式。
浮点数有主要两种类型,分别是float和double(long double这里不讨论)。float表示单精度浮点数,在计算机中用4个字节存储;double表示双精度浮点数,在计算机中用8个字节存储。在实际存储时,这些字节又分成三个部分,分别用于存储特定的数据。
float:
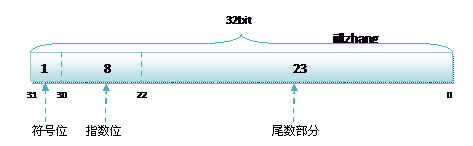
float一共有32个bit。第一个bit存储的数据用于表示符号位。正数为0,负数为1。后面8位是指数位,最后23位为尾数。这里的指数和尾数又分别是什么呢?我们来看一个浮点数9.825。将其转换成二进制:
先看整数9,它转换成二进制是1001。小数部分0.825转换为小数是110100110011001…后面1001无限下去。
0.825 * 2 = 1.65 取1
0.65 * 2 = 1.3 取1
0.3 * 2 = 0.6 取0
0.6* 2 = 1.2 取1
0.2 * 2 = 0.4 取0
0.4* 2 = 0.8 取0
0.8 * 2 = 1.6 取1
0.6* 2 = 1.2 取1
0.2 * 2 = 0.4 取0
0.4* 2 = 0.8 取0
0.8 * 2 = 1.6 取1
…这里会无限循环下去
所以,9.825转换为小数就是1001.11010011001100110011…,把其用科学计数法表示(这里的底为2)为1.00111010011001100110011 * (2^3)。这里【00111010011001100110011】这部分就是9.825这个浮点数在计算机中存储时的尾数部分,如果尾数不足23位,则在后面补0。(注意,由于整数部分总是为1,所以省去不存储)。指数部分是3,其也称为浮点数的阶码。阶码是用移码-1来得出的。移码与补码相似,只是其符号位用1表示正数,用0表示负数。移码的定义式为([x]为x的移码):
[x]=2^(n-1) + x (-2^(n-1) ≤x<2^(n-1))其中n表示阶码的存储位数。对于float而言,n等于8。
[3] = 10000011,用公式计算的话就是2^7 + 3 = 131。再减去1,得10000010(十进制就是130)。
所以9.825在计算机中存储为:0 10000010 00111010011001100110011。计算机在需要进位时,实际是以这个32位的二进制串为基础,根据“四舍六入五成双”的规则来计算的。根据这个32位的二进制串计算得到的实际小数部分(11010011001100110011)的十进制为0.82499980926513671875,根据<=4舍入的规则,最后结果的小数部分为0.82。而9.845的存储二进制为0 10000010 00111011000010100011111,其实际小数部分(11011000010100011111)的十进制是0.84500026702880859375,根据5后面有有效数字则进1的规则,最后结果的小数部分为0.85。
double类型的存储方式与float类型的相似,只是double类型一共有64bit,其中1bit表示符号位,11bit表示指数部分,剩余52bit表示尾数。
附:
十进制整数转换位二进制:(除2取余法)
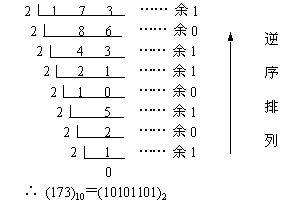
这里需要注意的是,余数是逆序排列的。上图中的结果就是10101101,而不是10110101。
十进制小数转换为二进制的方法如下:(乘2取整)
