目录
前言
????????函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数?main()?。函数声明告诉编译器函数的名称、返回类型和参数。函数定义提供了函数的实际主体。
? ? ? ? 函数的参数:分为形参和实参。具体的用法在程序中体现。不过可以这样理解,形参实例化之后其实相当于实参的一份临时拷贝。
? ? ? ? 函数的声明和定义:函数声明会告诉编译器函数名称及如何调用函数。函数的实际主体可以单独定义。. 函数的声明一般出现在函数的使用之前。要满足先声明后使用。函数的声明一般要放在头文件中的。
? ? ? ? 函数递归:程序调用自身的编程技巧称为递归,通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。递归的两个必要条件。具体用法在编程中体现。
1.存在限制条件,当满足这个限制条件的时候,递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件。
一、函数的基本用法
1.写一个函数,作用是交换输入的两个整数。
#include <stdio.h>
void change1(int x,int y){
int tem=0;
tem=x;
x=y;
y=tem;
}
void change2(int* x,int* y){ //此处的*为解引用操作,表示根据指针地址找到对应内存空间
int tem=0;
tem=*x;
*x=*y;
*y=tem;
}
int main()
{
int a=10;
int b=20;
change2(&a,&b);
printf("%d,%d\n",a,b);
return 0;
}
/*
实参a,b和形参x,y没有任何关系(唯一的联系就是形参x,y创建的时候通过实参a,b初始化)
所以调用函数change的时候交换的是x,y。需要交换的a,b并没有交换。
解决问题的办法就是让函数内部就能访问到a,b
*/
2.写一个函数实现冒泡排序
#include <stdio.h>
void bubbleSort(int arr[],int size){
int tmp=0;
for(int count=0;count<size;count++){
for(int i=0;i<size-1-count;i++){
if(arr[i]>arr[i+1]){
tmp=arr[i];
arr[i]=arr[i+1];
arr[i+1]=tmp;
}
}
}
}
int main()
{
int arr[]={2,5,9,4,3,7,23,4,11,45,76,2,1};
bubbleSort(arr,sizeof (arr)/sizeof (arr[0]));
for(int i=0;i<sizeof (arr)/sizeof (arr[0]);i++){
printf("%d\n",arr[i]);
}
return 0;
}
二、递归
1.递归求一个整数的阶乘
#include <stdio.h>
int fac(int n){
if(n==1||n==0){
return 1;
}else{
return n*fac(n-1);
}
}
int main(){
int a=5;
printf("%d\n",fac(a));
return 0;
}2.递归和非递归实现斐波那契数列
#include <stdio.h>
int fib1(int n){
if(n==1||n==2){
return 1;
}
else{
return fib1(n-1)+fib1(n-2);
}
}
int fib2(int n){
if(n==1||n==2){
return 1;
}
int last1=1;
int last2=1;
int cur=0;
for(int i=3;i<=n;i++){
cur=last1+last2;
last2=last1;
last1=cur;
}
return cur;
}
int main()
{
printf("%d\n",fib1(10));
printf("%d\n",fib2(10));
return 0;
}注:递归实现斐波那契数列比较容易想到,但是我们可以发现递归实现斐波那契数列会存在大量的重复的计算,于是我们使用循环实现斐波那契数列,这样重复的计算会少很多。程序的运行速度一般来说和是否递归和循环没有太大关系,主要是看重复运行的次数。我们们需要灵活合理的使用递归以及循环。
3.顺序打印一个数的每一位
#include <stdio.h>
void printNum(int num){
if(num>=10){
printNum(num/10);
}
printf("%d\n",num%10);
}
int main()
{
int a=2131345;
printNum(a);
return 0;
}
4.计算一个数的每一位之和(例:输入2131345输出19)
#include <stdio.h>
int digitSum(int n){
if(n<10){
return n%10;
}else{
return n%10+digitSum(n/10);
}
}
int main()
{
printf("%d\n",digitSum(1792));
return 0;
}5.递归和非递归实现求字符串的长度
#include <stdio.h>
int myStrLen(char* str){
int len=0;
while(str[len]!='\0'){
len++;
}
return len;
}
int myStrLen2(char* str){
if(str[0]=='\0'){
return 0;
}else{
return myStrLen2(str+1)+1;
}
}
int main(){
printf("%d\n",myStrLen("qwerty"));
printf("%d\n",myStrLen2("qwerty"));
return 0;
}6.编写一个函数,递归实现将字符串中的字符反向排列(不是逆序打印)
思路:假如第一次传入abcdef,交换首尾得到fbcdea,传入bcde,再交换首尾.....直到字符串长度小于2。我们会发现,正确的把参数传入下次函数调用变得很复杂。于是我们换一种思路。
? ? ? ? 同样第一次传入abcdef,将首字符的值用中间变量保存,然后将首字符改为f,尾字符改为'\0'。将str+1传入到下次调用的时候。(此时字符串长度-1,因为'\0'提前了)这样每次中间变量都会将当前首字符的值保存,直到传入的字符串的长度小于2的时候,我们结束递归,当前为{'d','\0'}我们将中间变量保存的值c赋给'd'后面的字符'\0',然后回归到上次调用,继续将中间变量的值赋给后面的'\0'......这样我们就得到了反转之后的字符串。
#include <stdio.h>
#include <string.h>
void reverse_string(char* str){
//保存字符串的首字符
char begin=*str;
//首字符变为尾字符,尾字符变为'\0'
*str=*(str+strlen(str)-1);
*(str+strlen(str)-1)='\0';
//判断递归
if(strlen(str+1)>=2){
reverse_string(str+1);
}
//'\0'变为首字符(此时的strlen比之前小1)
*(str+strlen(str))=begin;
}
int main()
{
char str[] = "abcdef";
printf("%s\n",str);
reverse_string(str);
printf("%s\n",str);
return 0;
}
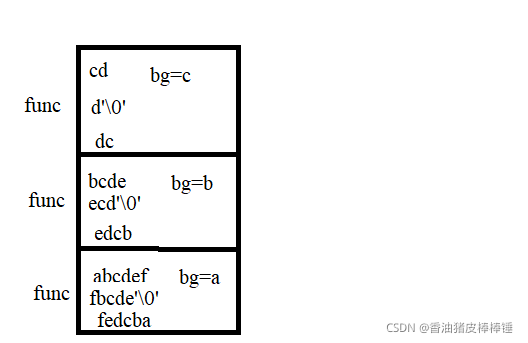
?建议通过画图的方式方便自己进一步来理解。
递归,我们不能将‘递’和‘归’割裂开,更应当思考‘递’和‘归’过程中我们应当怎么操作来达到目标。往往我们会将‘归’的过程给忽视,但是只有两部分一起思考才能达到最好的效果。