一、参考文章

C++文件类（文件流类）及用法详解

C++下string类型转double类型

最小二乘法求解直线方程系数

最小二乘法拟合直线-C++实现

二、文件流操作

3个文件流类，分别为：
ifstream：专用于从文件中读取数据；
ofstream：专用于向文件中写入数据；
fstream：既可用于从文件中读取数据，又可用于向文件中写入数据。
这 3 个文件流类都位于 fstream 头文件中。

继承关系
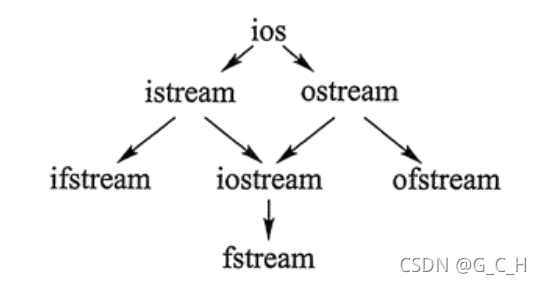
由上图可以看出，ifstream 类和 fstream 类是从 istream 类派生而来的。

打开文件可以通过以下两种方式：

调用流对象的 open 成员函数打开文件。

在流对象上执行 open 成员函数，给出文件路径和打开模式，就可以打开文件。

	ifstream infile;
    infile.open("c:\\tmp\\test.txt", ios::in);

定义文件流对象时，通过构造函数打开文件。

在构造函数中给出文件路径和打开模式也可以打开文件。

ifstream infile("c:\\tmp\\test.txt", ios::in);

判断文件打开是否成功，有两种方式：

可以看 “对象名” 这个表达式的值是否为 true，如果为 true，则表示文件打开成功。

if (infile)

也可以使用成员函数 fstream::is_open()，同样是返回一个bool值。

if (inflie.isopen())

当不再对打开的文件进行任何操作时，应及时调用 close() 成员方法关闭文件。

调用 open() 方法打开文件，是文件流对象和文件之间建立关联的过程。
调用 close() 方法关闭已打开的文件，是切断文件流对象和文件之间的关联。

附上代码：

	...

	string str;
	ifstream infile("data.txt", ios::in);	//写入文件 ros::out
	if (!infile) {
		cout << "文件读取失败!" << endl;
		return -1;
	}
	int num_point = 0;
	vector<double> xi, yi, xi2, xiyi;
	
	// istream& getline(?istream& is,?string& str,?char delim?)
	while (getline(infile, str)) {	// 读取一行的数据，并放入字符串 str 中	
		stringstream data_flow(str);	// 将整行字符串 str 读入到字符串流 data_flow 中
		string str_tmp;

		getline(data_flow, str_tmp, ',');
		xi.push_back(stod(str_tmp));	// stod 用于string 转 double
		xi2.push_back(pow(xi.back(), 2));

		getline(data_flow, str_tmp, '\0');
		yi.push_back(stod(str_tmp));
		xiyi.push_back(xi.back() * yi.back());

		num_point++;
	}
	infile.close();

	...

三、最小二乘法拟合

核心思想是使得估计出的模型与实际数据之间误差的平方和最小（趋于0）,以“残差平方和最小”确定直线位置。
在误差方程的一阶导数等于0处，误差函数取得极值。具体公式可参考第三篇引用文章。

附上代码：

main.cpp

	...
	
	double tmp_xi = 0, tmp_yi = 0, tmp_xi2 = 0, tmp_xiyi = 0;
	for (int i = 0; i < xi.size(); i++) {
		tmp_xi += xi.at(i);
		tmp_yi += yi.at(i);
		tmp_xi2 += xi2.at(i);
		tmp_xiyi += xiyi.at(i);
	}
	
	Least_Squares LS(num_point, tmp_xi2, tmp_xi, tmp_xiyi, tmp_yi);

	double k, b;
	k = LS.compute_k();
	b = LS.compute_b();
	if (k == 0 && b == 0) {
		cout << "分母存在为0的情况" << endl;
	}

	cout << "k = " << k << "," << "b = " << b << endl;
	
	...

fitting.h

#ifndef _FITTING_H
#define _FITTING_H

#include <iostream>
#include <fstream>
#include <string>
#include <vector>
#include <cmath>
#include <sstream>

using namespace std;

class Least_Squares {
public:
	Least_Squares(int num, double sum_xi2, double sum_xi, double sum_xiyi, double sum_yi);
	~Least_Squares() {};

	double compute_k();
	double compute_b();

private:
	int m_num;
	double m_sum_xi2;
	double m_sum_xi;
	double m_sum_xiyi;
	double m_sum_yi;
};

#endif // !_FITTING_H

fitting.cpp

#include "fitting.h"

Least_Squares::Least_Squares(int num, double sum_xi2, double sum_xi, double sum_xiyi, double sum_yi)
							:m_num(num), 
							m_sum_xi2(sum_xi2), 
							m_sum_xi(sum_xi),
							m_sum_xiyi(sum_xiyi), 
							m_sum_yi(sum_yi){

}

double Least_Squares::compute_k() {
	if ((m_sum_xi2 * m_num - m_sum_xi * m_sum_xi) != 0)
		return (m_sum_xiyi * m_num - m_sum_xi * m_sum_yi) / (m_sum_xi2 * m_num - m_sum_xi * m_sum_xi);
	else
		return 0;
}

double Least_Squares::compute_b() {
	if ((m_sum_xi2 * m_num - m_sum_xi * m_sum_xi) != 0)
		return (m_sum_xi2 * m_sum_yi - m_sum_xiyi * m_sum_xi) / (m_sum_xi2 * m_num - m_sum_xi * m_sum_xi);
	else
		return 0;
}