[C++知识库]欧拉方法与改进欧拉方法(C++实现)

综述：

????????在一阶常微分方程的数值解法中 ，常采用的欧拉方法，欧拉方法局部截断误差为O(2)，所以欧拉方法是一阶方法，改进后的欧拉方法截断误差为O(3),所以改进后的欧拉方法是二阶方法，精度更高。本文将以具体一微分方程为例，使用C++分别采用欧拉方法和改进后的欧拉方法对其求解。

目录

综述：

题目：

求解：

一、欧拉方法

二、改进欧拉方法

代码实现：

运行结果：

计算结果比较：

题目：

求初值问题：

求解：

一、欧拉方法

step1:

利用差商代替?得

step2:

用表示的近似值，用表示的近似值，变为：

二、改进欧拉方法

step1:

先用显式欧拉公式作预测，算出

step2:

再将代入隐式梯形公式的右边做校正得到

?为了方便编程计算，我们还可以将改进的欧拉公式写成：

代码实现：

公式比较简单，代码实现起来也很简单

#include <iostream>
#include <iomanip>
using namespace std;

class Euler
{
public:
	/*Euler()
	{

	}*/
	Euler(double x0,double y0,double h,int n)
	{
		this->h = h;
		this->x = x0;
		this->y = y0;
		this->m_n = n;
	}
	double fun(double x, double y)
	{
		return (y - (x * 2.0) / y);
	}
	void Eulerfun()
	{
		double yn_next = 0.0;
		int n = this->m_n;
		while (n)
		{
			yn_next = this->y + this->h * fun(this->x, this->y);
			
			cout <<"n = "<<this->m_n-n+1 << "时：\t" << "yn = " << setprecision(7) << yn_next << endl;
			this->x += this->h;
			this->y = yn_next;
			n--;
		}
	}
	double x;
	double y;
	double h;
	int m_n;
};

class EulerPro :public Euler
{
public:
	/*EulerPro():Euler(0, 1, 0.1, 10)
	{
	
	}*/
	EulerPro(double x0, double y0, double h, int n):Euler(0,0,0,0)
	{
		this->h = h;
		this->x = x0;
		this->y = y0;
		this->m_n = n;
	}
	void EulerProfun()
	{
		double yn_next, yp, yc;
		yn_next = yp = yc = 0.0;

		int n = this->m_n;
		while (n)
		{
			yp = this->y + this->h * fun(this->x, this->y);
			yc = this->y + this->h * fun(this->x + h, yp);
			yn_next = (yp + yc) / 2;
			
			cout << "n = " << this->m_n - n + 1 << "时：\t" << "yn = "<<yn_next << endl;
			this->x += this->h;
			this->y = yn_next;
			n--;
		}
	}
};
int main()
{
	cout << "--------------欧拉方法--------------" << endl;
	cout << endl;
	Euler e(0, 1, 0.1, 10);
	e.Eulerfun();
	cout << endl;
	cout << "--------------改进欧拉--------------" << endl;
	cout << endl;
	EulerPro ep(0, 1, 0.1, 10);
	ep.EulerProfun();
	return 0;
}

运行结果：

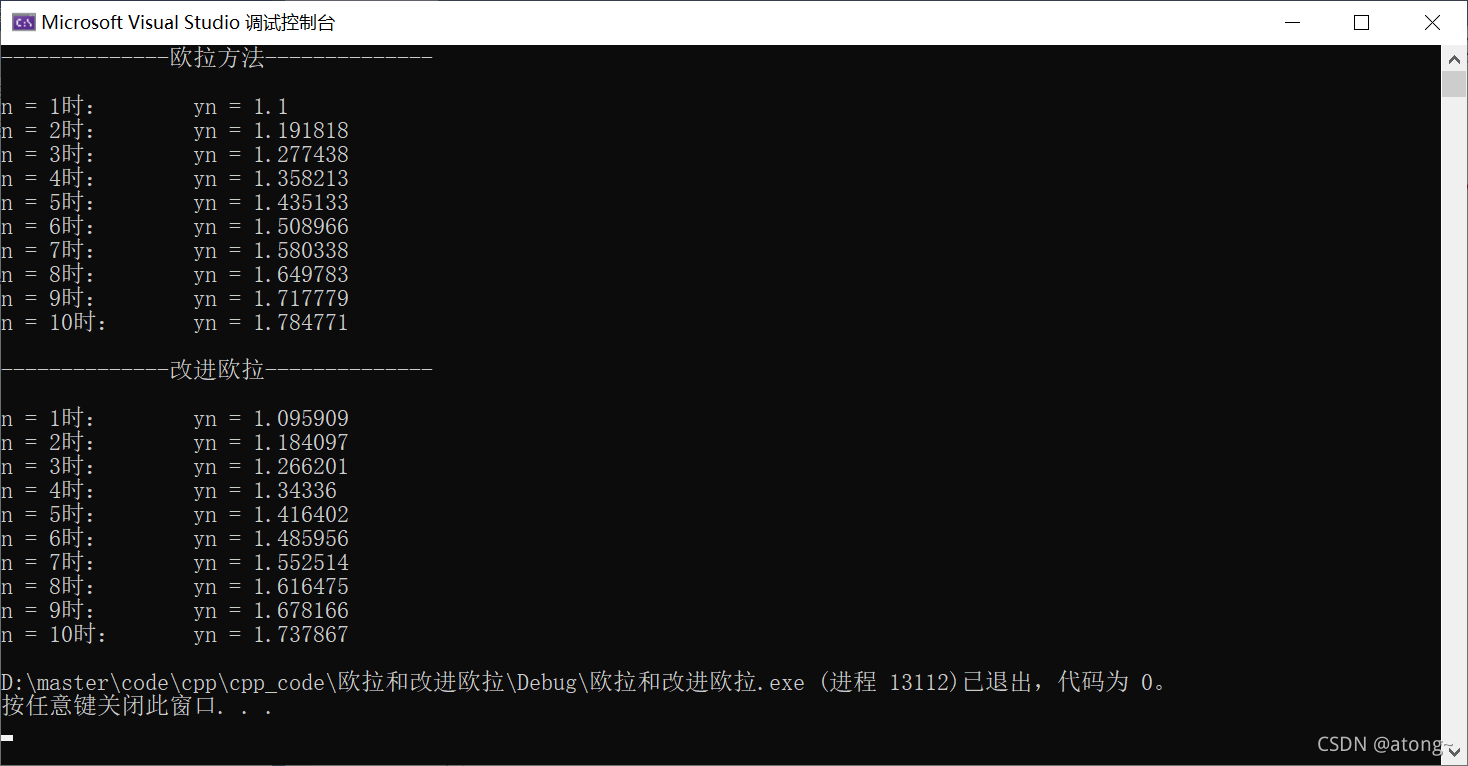
计算结果比较：

n		欧拉方法	改进的欧拉方法	精确解
0	0	1	1	1
1	0.1	1.1	1.095909	1.095445
2	0.2	1.191818	?1.184097	1.183216
3	0.3	1.277438	1.266201	1.264991
4	0.4	?1.358213	1.34336	1.341641
5	0.5	1.435133	1.416402	1.414214
6	0.6	?1.508966	1.485956	1.483240
7	0.7	1.580338	?1.552514	1.549193
8	0.8	?1.649783	1.616475	1.612452
9	0.9	1.717779	?1.678166	1.673320
0	1	1.784771	1.737867	1.763051

明显看出，改进的欧拉方法算出的结果更接近真实结果，并且，改进的欧拉方法比欧拉方法的精度提升了一位。