[C++知识库]c++实现哈夫曼树以及哈夫曼编码

介绍

哈夫曼树-----即最优二叉树，带权路径长度（WPL）最小的二叉树，经常应用于数据压缩。
对于普通需要将字符串编码传输时，普通的编码需要将每个字符编程定长的二进制格式，但是每个字符在数据中通常出现的概率不同的，所以，需要使用不定长的二进制表示是编码的表示更短。

前缀编码：对于每个字符设计长度不等的编码，必须使任一字符的编码都不是另一个字符的前缀。这样才能让编码不出现二义性。
Huffman编码：是前缀编码，也是最短编码—>压缩率最高。且是无损压缩！！！

连续存储方式建立Huffman树

//树结点结构
struct  Node
{
    double weight; //权重
    int parent,lson,rson;   //父结点、左孩子、右孩子下标
};

//初始化
void init(vector<double>& nums,Node* huff)
{
    int n=nums.size();
    //从下标1开始
    for(int i=1;i<=n;i++){
        huff[i].parent=0;
        huff[i].lson=0;
        huff[i].rson=0;
        huff[i].weight=nums[i-1];
    }
}
//从当前所有父结点为0的节点中选择权重最小的两个结点A，B
vector<int> select(Node* huff,int len)
{
    int pA=0,pB=0;
    double MinA=INT32_MAX,MinB=INT32_MAX;

    for(int i=1;i<len;i++){
        if(!huff[i].parent && huff[i].weight){
            if(MinA>huff[i].weight){
                pB=pA;pA=i;
                MinB=MinA;MinA=huff[i].weight;
            }
            else if(MinB>huff[i].weight){
                pB=i;MinB=huff[i].weight;
            }
        }
    }
    return {pA,pB}; //返回对应结点的下标
}

//哈夫曼树共有2*n-1个结点
//前面n个结点是叶子结点，后面n-1个节点是构造出来的父节点
Node* build(vector<double>& nums)
{
    int n=nums.size();
    Node* huffTr=new Node[2*n];

    init(nums,huffTr);  //初始化---1、构造森林全是根

    for(int i=n+1;i<=2*n-1;i++){

        //从当前所有父结点为0的节点中选择权重最小的两个结点A，B---2、选择两小造新树
        vector<int> ans=select(huffTr,2*n);
        int j=ans[0],k=ans[1];

        //生成新的结点，并把该节点的左右子树设置A，B---3、删除两小添新人
        huffTr[i].weight=huffTr[j].weight+huffTr[k].weight;
        huffTr[i].parent=0;
        huffTr[i].lson=j;
        huffTr[i].rson=k;

        //设置A，B的父结点
        huffTr[j].parent=i;
        huffTr[k].parent=i;
        //---4、重复2、3剩单根
    }
    return huffTr;
}

建树与编码的测试代码

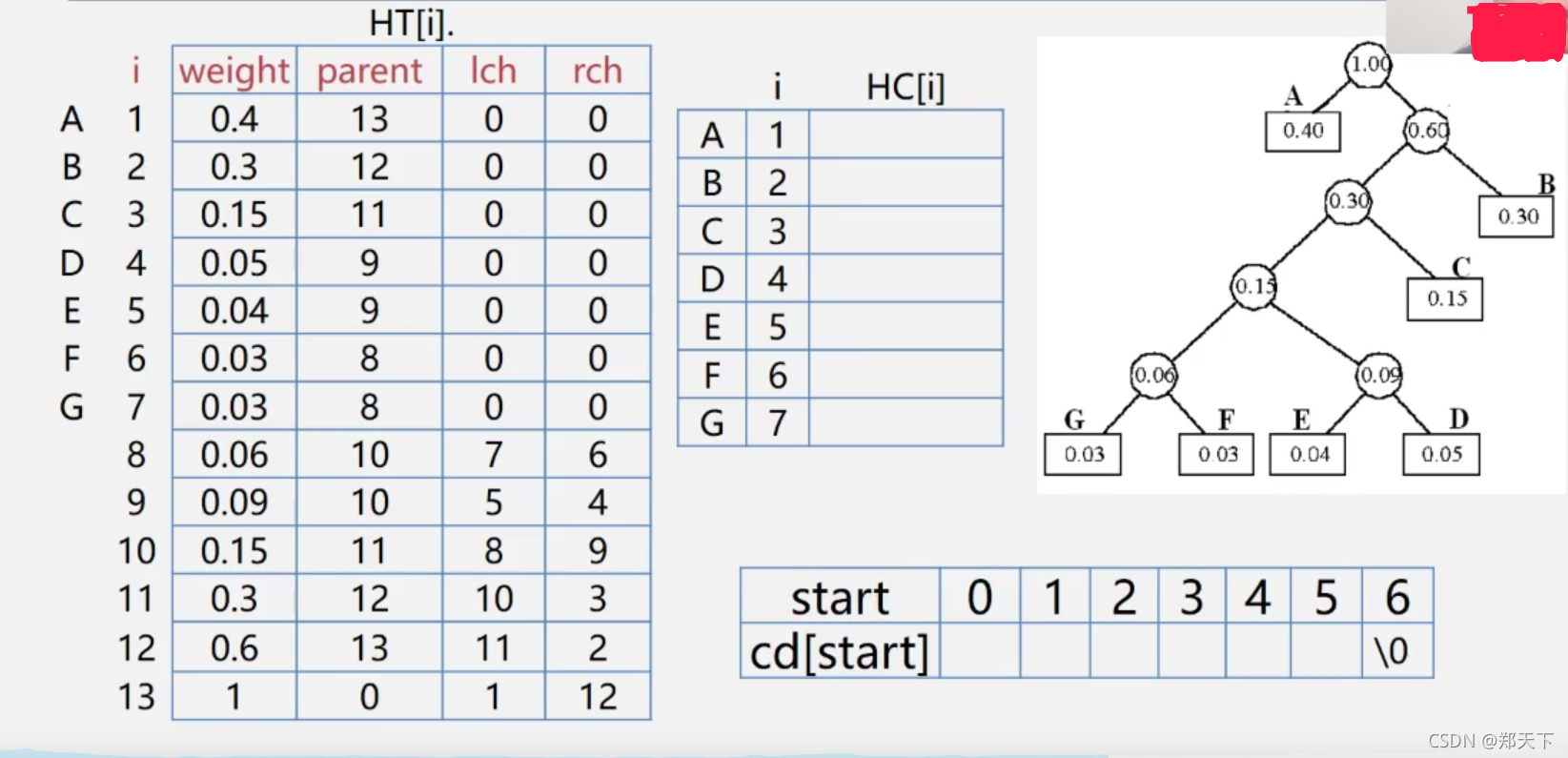
int main()
{
    //测试用例1：
    //A、B、C、D、E、F、G字符对应的概率（即权重）用数组nums表示
    vector<double> nums={0.4,0.3,0.15,0.05,0.04,0.03,0.03};
                        //A,B,C,D,E,F,G
    int n=nums.size();

    auto huff=build(nums);  //构建Huffman树
    //遍历
    for(int i=1;i<=2*n-1;i++){
        cout<<huff[i].weight<<" "<<huff[i].parent<<" "<<huff[i].lson<<" "<<huff[i].rson<<endl;
    }
    cout<<endl;

    //测试用例2：
    //将ABCDEFG字符串进行Huffman编码，从底向上遍历
    vector<string> res;
    for(int i=1;i<=7;i++){
        string a;
        int cur=i;
        //遍历到根节点时退出循环（根节点的parent为0），说明该字符的编码已完成
        while(huff[cur].parent!=0){
            int par=huff[cur].parent;
            //当前结点是其父结点的左孩子，则标0;是右孩子则标1
            if(huff[par].lson==cur){
                a='0'+a;
            }else{
                a='1'+a;
            }
            cur=par;
        }
        res.emplace_back(a);
    }
    //打印每个字符的编码
    for(int i=1;i<=7;i++){
        char c=i-1+'a';
        cout<<c<<" :"<<res[i-1]<<endl;
    }

    return 0;
}