一. 知识讲解
1.1 迭代
??迭代是一个反复反馈的过程,每次计算都是基于前一次的计算机果进行的,其目的通常是为了不断接近某个结果。
例如计算前n项和:
#include <stdio.h>
int main(){
int n;
while(~scanf("%d", &n)){
int Sn = 0;
for(int i = 1; i <= n; i++){
Sn += i;
}
printf("%d\n", Sn);
}
return 0;
}
1.2 递归
??递归其实就是重复调用某个函数,通常是将一个大问题转化为一个个子问题通过重复相同的几个操作解决问题
例如求n!
#include <stdio.h>
int Factorial(int n){
if(n == 1){
return 1;
}
return Factorial(n - 1);
}
int main(){
int n;
while(~scanf("%d", &n)){
printf("%d\n", Factorial(n));
}
return 0;
}
二. 课后习题
2.1 阶乘尾数
面试题 16.05. 阶乘尾数
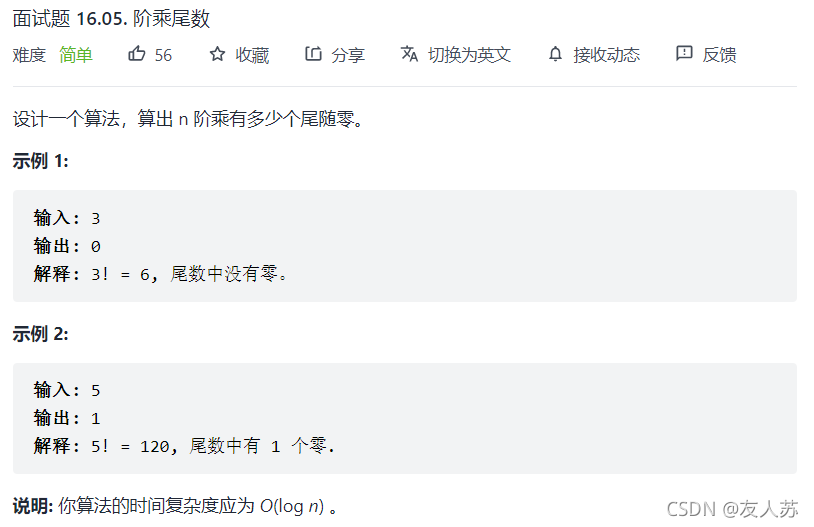
统计有多少个0,实际上只需要统计有多少对2和5,因为只有2*5等于10,但又因为2的数量一定比5大,所以我们只需统计5的数量即可,将所有5的倍数拆分为5,并统计。
代码如下:
int trailingZeroes(int n){
if(n < 5){
return 0;
}
long cnt = 0;
for(long i = 5; n / i > 0; i *= 5){
cnt += n / i;
}
return cnt;
}

2.2 斐波那契数
509. 斐波那契数
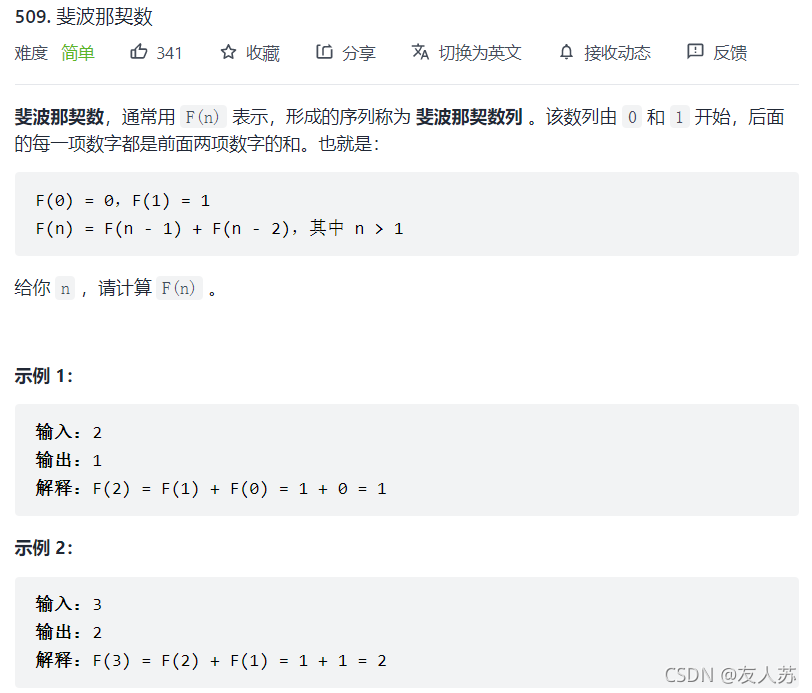

通过分析我们可以得知,对于每个F(n)的状态都是前面两个数的和,所以可以得到其状态方程为:F(n) = F(n - 1) + F(n - 2)
而初始条件为:F(1) = F(2) = 1;
代码如下:
int fib(int n){
if(n == 0){
return 0;
}
if(n == 1 || n == 2){
return 1;
}
return fib(n - 1) + fib(n - 2);
}
