问题描述:
在n×n的方格棋盘上,放置n个皇后,要求n个皇后两两不在一行,不在一列,不在同一对角线上
?PS:
行不用检测,因为皇后本身就是一行一行往下放的,并且一行只能放一个,所以当放好一个皇后后,只需检测列及对角线的位置有无皇后??,如下图这些位置
?
思路 【回溯法】
1.? ?从棋盘的第一行开始,依次遍历所有位置,依次判断当前位置是否能够放置皇后,判断的依据为:同该行之前的所有行中皇后的所在位置进行比较,是否在同一列,或者在同一条斜线上(斜线有两条,为正方形的两个对角线)。
2.? ?如果该行所有位置都不符合要求,则回溯到上一行,改变皇后的位置,继续试探。直到在当前行找到下一个合法位置。
3.? ?如果试探到最后一行,所有皇后摆放完毕,且找到了放置皇后的合法位置,那么解的个数加一,并再次回溯。最后一定要记得将棋盘恢复原样,避免影响下一次摆放。?
画一个更大的图方便我们找规律(以8皇后为例):
假设我在蓝色圆圈的这一行放皇后,那么就要检测这一列以及它的斜上斜下对角线,写出每个方格坐标我们可以发现,左上对角线坐标和相等,左下对角线差相等?
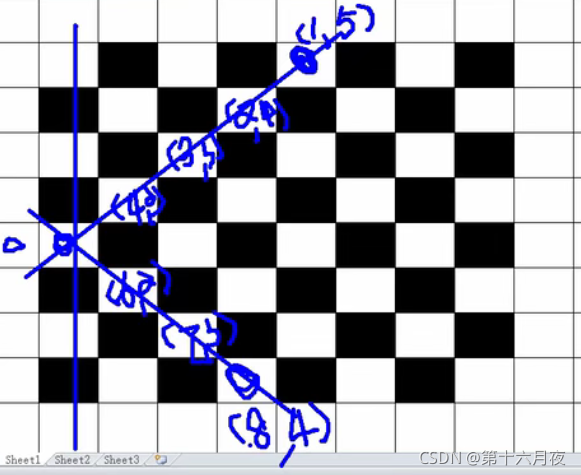
?假设我将皇后放在蓝色位置,那么我只需要查看蓝色这一行之前的所有行有没有放过(因为是一行一行放的,蓝色之后的行肯定没有)

对于n*n的棋盘,从第一行第一列开始放置皇后,然后在第二行,从左至右,找到第一个可以放置皇后的位置并放置一个皇后。那么什么时候会遇到一点问题呢?一种情况是,我在某一行找不到放置皇后的合法位置了;另一种情况是,每一行都放置了一个皇后,此时已经构成了一个解,需要寻找下一个解。对于第一种情况,我们需要把当前行的上一行的皇后移除,在代码上的表现,就是把a[i]的位置设置为上一行的皇后位置并从这个位置继续向右,找到第一个可以放置皇后的位置,并放置之;对于第二种情况,其实前半部分处理与第一种情况相同,但是不要忘记在返回的count加上一(因为此时已经有了一个解)
?
补充?
回溯法,又被称为“试探法”。解决问题时,每进行一步,都是抱着试试看的态度,如果发现当前选择并不是最好的,那么就回退一步重新选择。这种走不通就回退再走的方法就是回溯法。?
回溯和递归其实并不是一回事,它们之间唯一的联系就是,回溯法可以用递归思想实现。
代码?
#include <stdio.h>
const int N=10; //最多的皇后个数
int a[N];//a[i]表示第i行上的皇后放于a[i]列上,如a[3]=7表示第3行的皇后放在第7列上
int count,n; //存放解的个数
//测试在(x,y)位置能不能放皇后
bool check(int x,int y){
for(int i=1;i<=x;i++){
if(a[i]==y) return false; //判断是否同列(false,第i列已经放过)
if(i+a[i]==x+y) return false; //斜上对角线(右对角线)已经放过
if(i-a[i]==x-y) return false; //斜下对角线(左对角线)已经放过
}
return true; //以上三种情况都没有,说明该位置可以放皇后
}
//输出解的情况
Print(int n){
count++; //先记得个数+1
printf("第%d种解",count);
for(int i=1;i<=n;i++){
printf("(%d,%d)",i,a[i]);
}
printf("\n");
}
//从放第row行开始求解n皇后的解
void dfs(int row){
if(row>n) { //row>n 也可以写成row==n+1
Print(n); // 表示超过了n行到达了边界,说明产生了一组解 ,直接输出
return ;
}
for(int i=1;i<=n;i++){
if (check(row,i)){ //检查是否冲突
a[row]=i; //不冲突,将皇后放在i列上
dfs(row+1); //进入下一行(递归调用后面的皇后)
a[row]=0; //递归完毕后,还原第row行避免重复,所以进入下一行时吧刚才的row变为0,因为有多组解【回溯】
}
}
}
int main(){
printf("输入n*n的棋盘数:");
scanf("%d",&n);
dfs(1); //因为从第一行开始
printf("一共有%d种解",count);
return 0;
} 