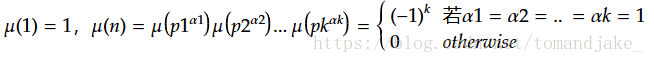写在开头:
待补
打完这四场比赛就补。
算法
markdown 语法网址:https://www.zybuluo.com/codeep/note/163962#cmd-markdown-%E5%85%AC%E5%BC%8F%E6%8C%87%E5%AF%BC%E6%89%8B%E5%86%8C
报错
bool operator <(struct node &b)const
{
return r-l<b.r-b.l;//等号可能会错
}
比赛模板
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define il (i<<1)
#define ir (i<<1)+1
#define pb push_back
const int maxn=1e5+5;
inline char nc() {static char buf[1000000],*p1=buf,*p2=buf;return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;}
inline void read(int &sum) {char ch=nc();sum=0;while(ch<'0') ch=nc();while(ch>='0') sum=(sum<<3)+(sum<<1)+(ch^48),ch=nc();}
ll qsm(ll a,ll b)
{
ll base=a,ans=1;
while(b>0)
{
if(b%2==1)ans=ans*base;
base=base*base;
b>>=1;
}
return ans;
}
ll gcd(ll a,ll b)
{
return b==0?a:gcd(b,a%b);
}
void solve()
{
}
int main()
{
ios::sync_with_stdio(false);
int t;
cin>>t;
while(t--)sovle();
return 0;
}
STL
unordered_mapPostgraduate entrance examinatio
ceil()向上取整
floor()向下取整
__builtin_popcount()
用于一个数字的二进制中有多少个1.
bitset
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const LL mod = 1000000007;
const int MX = 1e3+1;
bitset<100*100*100+1>ans,t;
int main(){
int n;scanf("%d",&n);
ans[0]=1;
while(n--){
t.reset();
int l,r;scanf("%d%d",&l,&r);
while(l<=r){
t|=ans<<(l*l);l++;
}
ans=t;
}
printf("%d",ans.count());
return 0;
}
字符串操作
getline(cin,s);
to_string();
stoi/stol/stoll;
优先队列
priority_queue <int> q;
q.size();//返回q里元素个数
q.empty();//返回q是否为空,空则返回1,否则返回0
q.push(k);//在q的末尾插入k
q.pop();//删掉q的第一个元素
q.top();//返回q的第一个元素
q.back();//返回q的末尾元素
priority_queue<int> da; //大根堆
priority_queue<int,vector<int>,greater<int> > xiao; //小根堆
pair
震惊,map竟然是用pair 实现的。
#include <iostream>
#include <string>
#include <utility>
#include <map>
using namespace std;
int main() {
pair<string, string> p1("sc0301","小杨"); // 方式一,创建一个pair名为p1
pair<string, string> p2 = make_pair("sc0302", "小马"); // 方式二,make_pair函数返回一个用"sc0302"和 "小马"初始化的pair
pair<string, string> p3("sc0303", "小王");
pair<string, string> p4("sc0304", "小何");
map<string, string> m1; // 创建一个空map
map<string, string> m2{ p1,p2,p3,p4 }; // 创建一个包含pair p1、p2、p3、p4的map
map<string, string> m3{ {"sc0301","小杨"},{"sc0302", "小马"},{"sc0303", "小王"},{"sc0304", "小何"} }; // 效果同上一句
map<string, string>::iterator it1 = m2.begin(); // 得到指向m2首元素的迭代器
map<string, string>::iterator it2 = m2.end(); // 得到指向m2尾元素的下一个位置的迭代器
pair<string, string> p11 = *it1; // 得到m2的首元素{"sc0301","小杨"},这是一个pair
string p1_ID = it1->first; // 得到m2的首元素{"sc0301","小杨"}的fisrt成员,学号
string p1_name = it1->second; // 得到m2的首元素{"sc0301","小杨"}的second成员,姓名
for (auto p : m2) {
cout << "学号:" << p.first << "; 姓名:" << p.second << endl;
}
m1.insert(p1); // 在map中插入已有的pair
m1.insert({ "sc0302", "小马" }); // 插入键值对{ "sc0302", "小马" }
m1.insert(pair<string, string> ("sc0303", "小王")); // 创建一个无名pair对象,并插入到map中
m1.emplace(p1); // 要插入的关键字已在容器中,emplace/insert什么都不做
m1.emplace(pair<string, string>("sc0303", "小王")); // 要插入的关键字已在容器中,emplace/insert什么都不做
map<string, string>::iterator it = m2.find("sc0301"); // 查找关键字为"sc0301"的元素,返回一个迭代器
if (it == m2.end()) { // 若"sc0301"不在容器中,则it等于尾后迭代器
cout << "未找到!" << endl;
}
else {
pair<string, string> result1 = *it; // 找到了
}
int result2 = m2.count("sc0305"); // 查找关键字为"sc0301"的元素,返回关键字等于"sc0301"的元素数量
if (result2==0) {
cout << "未找到!" << endl;
}
else {
cout << "找到了!" << endl;
}
}
sort排序
struct cmp
{
bool operator()(int a,int b)
{
return dist[a]>dist[b];
}
};
friend <返回类型> <函数名> (<参数列表>);
friend bool operator<(const node &a,const node &b)
{
return a.x<b.x;
}
bool operator<(node &a)const
{
return y<b.y;//y表示当前结构体的值
}
//**优先队列相反**
vector
vector<type> name;
a.clear(); //清空a中的元素
a.back(); //返回a的最后一个元素
a.front(); //返回a的第一个元素
vect.size();返回容器中元素的个数
vect.empty();判断容器是否为空
a.insert(a.begin()+1,5); //在a的第1个元素(从第0个算起)的位置插入数值5,
如a为1,2,3,4,插入元素后为1,5,2,3,4
vect.resize(num);重新指定容器的长度为num,若容器变长,则以默认值填充新位置。
如果容器变短,则末尾超出容器长度的元素被删除。
vect.resize(num,elem);重新指定容器的长度为num,若容器变长,则以elem值填充新位置。
如果容器变短,则末尾超出容器长度的元素被删除。
vect.push_back(1);//在vector最后添加元素1
a.swap(b); //b为向量,将a中的元素和b中的元素进行整体性交换
vect.pop_back()//删除最后一个元素
vector<int> vect(a,a+10);//将数组a整体插入;
sort(vect.begin(),vect.end());
for(int i=0;i<=b.size()-1;i++)
set
begin() //返回set容器的第一个迭代器
end() //返回set容器的最后一个迭代器
clear() //删除set容器中的所有的元素
empty() //判断set容器是否为空
max_size() //返回set容器可能包含的元素最大个数
size() //返回当前set容器中的元素个数
rbegin //返回的值和end()相同
rend() //返回的值和rbegin()相同
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int a[maxn];
int main() {
int n, q;
cin >> n >> q;
set<int>s;
while (q--)
{
int op, id;
cin >> op >> id;
s.insert(0); s.insert(n);
if (op == 1)s.insert(id);
else
{
set<int>::iterator it;
it = s.lower_bound(id);
int len = *it - *(--it);
cout << len << endl;
}
}
return 0;
}
二分查找
upper_bound:
//在一个已排序的序列中[first, last),返回第一个大于val的元素所在的地址。如果未找到结果,则返回last;
lower_bound:
//在一个已排序的序列[first, last), 返回第一个大于等于val元素的地址,如未找到,则返回last;
binary_search:
//在一个已排序的序列[first, last)中, 判断val是否存在;
unique
3 3 2 5 2 3 -》 3 2 5 2 3 3
python黑科技
eval()函数
可以直接求字符串表达式的值注意:“^”转“**”;
s = input()
s1=""
for i in range(len(s)):
if s[i]=="^" :
s1=s1+"**"
else :
s1=s1+s[i]
print(eval(s1))
常用函数
最 da公约数
ll gcd(ll a,ll b){
return b==0?a:gcd(b,a%b);
}
== __gcd()
快速幂
ll qsm(ll a,ll b)
{
ll base=a,ans=1;
while(b>0)
{
if(b%2==1)ans=ans*base;
base=base*base;
b>>=1;
}
return ans;
}
动态规划
数位dp
技巧 1:如果是从1->n,那么可以将区间问题转化为f(n)-f(m-1);
技巧2:利用数形结构来分析问题,注意last转移时的条件
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#define ll long long
using namespace std;
const int maxn=20;
ll f[maxn][maxn];
ll K;
void init()
{
for(int i=1; i<=9; i++) f[1][i]=1;
for(int i=2; i<maxn; i++){
for(int j=0;j<=9;j++)f[i][0]+=f[i-1][j];
for(int j=1; j<=9; j++)
{
f[i][j]+=f[i-1][j];
for(int k=j+K; k<=9; k++)
{
f[i][j]+=f[i-1][k];
}
}
}
}
ll dp(ll n)
{
if(!n) return 0;
vector<int>nums;
while(n) nums.push_back(n%10),n/=10;
ll res=0;//方案数
int last=0;
for(int i=nums.size()-1; i>=0; i--)
{
int x=nums[i];//x为当前这位数
// cout<<i<<" "<<x<<" "<<last<<" "<<res<<endl;
if(i==nums.size()-1)
{
for(int j=0; j<x; j++) //要保障比下一位>=上一位,所以从last开始枚举,最多枚举到x,last为上一位,也即最高位,对下一位的枚举是有限制的
res+=f[i+1][j];
last=x;
continue; //左端的节点有i+1个位数(因为第一位的下标是0)
}
if(x>last)
{
res+=f[i+1][last];
for(int j=last+K; j<x; j++)res+=f[i+1][j];
if(x>last&&x<last+K)break;
last=x;
} //如果当前这位数比上一位小,那么后面的都不成立了,直接break退出
else if(x==last)x=last;
else break;//如果能顺利到最后一个数说明树的最右边这一段的每一个数都是小于等于前一位数的,因而++
}
return res;
}
int main(void)
{
ll l,r,L,R;
cin>>l>>r>>K;
init();
cout<<dp(r)-dp(l-1)<<endl;
//cout<<f[4][1]<<endl;
return 0;
}
背包问题
背包问题一定是dp?
no!暴力搜索也能过背包问题,dp类似于记忆化搜索,如何有效利用已经被记录的信息是问题关键,如何保持信息的后续有效性也是关键。
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e4;
const int maxm=26;
int v[maxn],w[maxn],n,m,res=0,dp[maxm][maxn];
int dfs(int i,int j)
{
if(dp[i][j]!=-1)return dp[i][j];
if(i==m)
{
return 0;
}
else if(j<v[i])res=dfs(i+1,j);
else
{
res=max(dfs(i+1,j),dfs(i+1,j-v[i])+v[i]*w[i]);
dp[i][j]=res;
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=0;i<m;i++)cin>>v[i]>>w[i];
memset(dp,-1,sizeof(dp));
dfs(0,n);
cout<<res<<endl;
return 0;
}
01背包问题
一维数组需要逆序
二维需要对不操作的传递
bag[j]=maxv(bag[j],bag[j-w[i]]+v[i]);
完全背包问题
一维数组需要正序
maxValue[j] = max(maxValue[j], maxValue[j-w[i]] + v[i]);
多重背包问题
本质与01背包没有什么不同
分组背包问题
增加一维表示组别,保证只在这一组中选一个或者不选
数论
同余问题
定义:同余给定整数m,若用m去除两个整数a和b所得的余数相同,称a和b对模m同余,记作 a ≡ ? b ( m o d ? m ) a\equiv \ b(mod\ m) a≡?b(mod?m)?。
定理1 a ≡ b ( m o d ? m ) a\equiv b(mod\ m) a≡b(mod?m)当且仅当 m ∣ ( a ? b ) m|(a-b) m∣(a?b)
定理2 a ≡ b ( m o d ? m ) a\equiv b(mod\ m) a≡b(mod?m)当且仅当存在k满足 a = b + k m a=b+km a=b+km
定理3 同余关系是等价关系
定理4 若a, b, c是整数,m是整数,且
a
≡
b
(
m
o
d
?
m
)
a\equiv b(mod\ m)
a≡b(mod?m),则:
a
+
c
≡
a
+
c
(
m
o
d
?
m
)
a
?
c
≡
a
?
c
(
m
o
d
?
m
)
a
c
≡
b
c
(
m
o
d
?
m
)
a+c\equiv a+c(mod\ m)\\ a-c\equiv a-c(mod\ m)\\ ac\equiv bc (mod \ m)
a+c≡a+c(mod?m)a?c≡a?c(mod?m)ac≡bc(mod?m)
定理5 设a,b,c,d,为整数,m为正整数,若
a
≡
b
(
m
o
d
?
m
)
a\equiv b (mod\ m)
a≡b(mod?m),
c
≡
d
(
m
o
d
?
m
)
c\equiv d(mod\ m)
c≡d(mod?m),则
a
x
+
c
y
≡
b
x
+
d
y
(
m
o
d
?
m
)
(
即
可
加
性
)
a
c
≡
b
d
(
m
o
d
?
m
)
(
可
乘
性
)
a
n
≡
b
n
(
m
o
d
?
m
)
(
可
幂
性
)
f
(
a
)
≡
f
(
b
)
(
m
o
d
?
m
)
(
f
(
x
)
为
任
意
整
数
多
项
式
)
ax+cy\equiv bx+dy(mod\ m)(即可加性)\\ ac\equiv bd(mod\ m)(可乘性)\\ a^n\equiv b^n(mod\ m)(可幂性)\\ f(a)\equiv f(b)(mod\ m)(f(x)为任意整数多项式)
ax+cy≡bx+dy(mod?m)(即可加性)ac≡bd(mod?m)(可乘性)an≡bn(mod?m)(可幂性)f(a)≡f(b)(mod?m)(f(x)为任意整数多项式)
(ps:同余的性质十分稳定,具有线性。
定理6 设a,b,c,d为整数,m为正整数,则
- 若 a ≡ b ( m o d ? m ) a\equiv b(mod\ m) a≡b(mod?m),且d|m,则 a ≡ b ( m o d ? d ) a\equiv b (mod\ d) a≡b(mod?d)。(ps:当两数对m同余,对于m的因子也同余)
- 若 a ≡ b ( m o d ? m ) a\equiv b(mod\ m) a≡b(mod?m),则 g c d ( a , m ) = g c d ( b , m ) gcd(a,m)=gcd(b,m) gcd(a,m)=gcd(b,m)?
- a ≡ b ( m o d ? m i ) , i = 1 , 2 , … , n a\equiv b (mod\ m_i),i=1,2,\dots,n a≡b(mod?mi?),i=1,2,…,n成立,当且仅当 a ≡ b ( m o d [ m 1 , m 2 , … , m n ] ) a\equiv b (mod[m_1,m_2,\dots,m_n]) a≡b(mod[m1?,m2?,…,mn?]).
定理7 若 a c ≡ b c ( m o d ? m ) , d = g c d ( c , m ) ac\equiv bc(mod \ m),d=gcd(c,m) ac≡bc(mod?m),d=gcd(c,m),则 a ≡ b ( m o d ? m / d ) a\equiv b (mod \ m/d) a≡b(mod?m/d)
扩展欧几里得
贝祖定理:如果a\b是整数,那么一定存在整数x,y使得 a x + b y = g c d ( a , b ) ax+by=gcd(a,b) ax+by=gcd(a,b)?有解
推论:如果 a x + b y = 1 ax+by=1 ax+by=1有解,那么 g c d ( a , b ) = 1 gcd(a,b)=1 gcd(a,b)=1
int exgcd(int a, int b, int &x0, int &y0)
{
if(!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a%b, y0, x0);
y -= a/b*x;
return d;
}
int main()
{
int a, b;
cin >> a >> b;
int x0, y0;
cout<<exgcd(a, b, x0, y0 )<<endl;
cout<<(x%b+b)%b<<endl;
return 0;
}
该函数的返回值为a和b的最大公因数d,其中x,y为其中一组解。
一次同余方程ax + by = c 有解的充要条件为 g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c
当 g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c是同余方程有 g c d ( a , n ) gcd(a,n) gcd(a,n)个解
x = x 0 + k ? b d x = x_0 +k*\frac{b}{d} x=x0?+k?db?
y = y 0 ? k ? a d y = y_0 -k*\frac{a}{d} y=y0??k?da?
欧拉函数
欧拉函数的定义
$\phi (n) $ 表示在1到n中,与n形成互质关系的数的个数。
欧拉函数的性质
-
当n为质数时, ? ( n ) = n ? 1 \phi(n)=n-1 ?(n)=n?1
-
欧拉函数是积性函数,但不是完全积性函数
只有当 n = p 1 ? p 2 n=p_1*p_2 n=p1??p2? 时, ? ( n ) = ? ( p 1 ) ? ? ( p 2 ) \phi(n)=\phi(p_1)*\phi(p_2) ?(n)=?(p1?)??(p2?)
? ( p q ) = ? ( q ) ? ? ( p ) = ( p ? 1 ) ( q ? 1 ) \phi(pq)=\phi(q)*\phi(p)=(p-1)(q-1) ?(pq)=?(q)??(p)=(p?1)(q?1)(RSA算法应用)
-
当n>2时, ? ( n ) \phi(n) ?(n)为偶数
当n为质数的k次幂时, ? ( n ) = p k ? p k ? 1 = ( p ? 1 ) p k ? 1 \phi(n)=p^k-p^{k-1}=(p-1)p^{k-1} ?(n)=pk?pk?1=(p?1)pk?1
证明,只用当数x为p的倍数时,两者才不互质,易得这类数的数量为 p k ? 1 p^{k-1} pk?1。
通过以上的理论可以得到以下公式,
?
(
N
)
=
N
?
∏
i
=
1
n
(
1
?
1
p
i
)
\phi(N) = N*\prod_{i=1}^{n}(1-\frac{1}{p_i})
?(N)=N?i=1∏n?(1?pi?1?)
其中pi为质因子,即每个质因子只算一次。
o(n)的筛法筛出质数的同时求得其函数值
需要用到如下性质:
设p为质数
如果p为x的因数
那么 ? ( p ? x ) = p ? x ? ( 1 ? 1 p 1 ) ? ( 1 ? 1 p 2 ) ? . . . ( 1 ? 1 p n ) ) = ? ( x ) ? p \phi(p*x)=p*x*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...(1-\frac{1}{p_n}))=\phi(x)*p ?(p?x)=p?x?(1?p1?1?)?(1?p2?1?)?...(1?pn?1?))=?(x)?p
如果p不是x的因数,即px互质
那么 ? ( p ? x ) = ? ( p ) ? ? ( x ) = ? ( x ) ? ( p ? 1 ) \phi(p*x)=\phi(p)*\phi(x)=\phi(x)*(p-1) ?(p?x)=?(p)??(x)=?(x)?(p?1)
phi[1]=1;
for(int i=2;i<=maxn;i++)
{
if(!isprime[i])
{
prime[++cnt]=i;
phi[i]=i-1;//质数直接能求出
}
for(int j=1;j<=cnt&&prime[j]*i<=maxn;j++)
{
isprime[i*prime[j]]=1;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];//px不互质
break;
}
else phi[i*prime[j]]=phi[i]*(prime[j]-1);//px互质
}
}
样例:
6 2
20 8
30 8
100 40
欧拉定理
a ? ( n ) ≡ 1 ( m o d ? n ) s . t . ? g c d ( a , n ) = 1 a^{\phi(n)}\equiv1(mod\ n)\\ s.t.\ gcd(a,n)=1 a?(n)≡1(mod?n)s.t.?gcd(a,n)=1
费马小定理
a
p
?
1
≡
1
(
m
o
d
?
p
)
a^{p-1}\equiv1(mod\ p)
ap?1≡1(mod?p)
由欧拉函数可知费马小定理为欧拉定理的特殊情况。
约数个数及约数和
当处理因子时,应当反向思考处理倍数。
d(n)为正整数n的因子个数。
s
u
m
(
n
)
sum(n)
sum(n)为约数之和
d
(
n
)
=
(
α
1
+
1
)
?
(
α
2
+
1
)
?
.
.
.
?
(
α
k
+
1
)
∑
i
=
1
i
=
质
数
个
数
∑
j
=
0
j
=
p
i
的
最
大
次
幂
p
i
j
d(n) = (\alpha_1+1)*(\alpha_2+1)*...*(\alpha_k+1) \\ \sum_{i=1}^{i=质数个数}\sum_{j=0}^{j=p_i的最大次幂} p_i^{j}
d(n)=(α1?+1)?(α2?+1)?...?(αk?+1)i=1∑i=质数个数?j=0∑j=pi?的最大次幂?pij?
N 在 2e9中,因子数最多1600个
中国剩余定理
中国剩余定理是对符合特定条件的线性同余方程组进行求解
中国剩余的解为构造解,非推理解
若
m
1
,
m
2
,
m
3
,
.
.
.
,
m
r
m_1,m_2,m_3,...,m_r
m1?,m2?,m3?,...,mr?是两两互素的正整数,则同余方程
x
≡
a
1
(
m
o
d
?
m
1
)
x
≡
a
2
(
m
o
d
?
m
2
)
x
≡
a
3
(
m
o
d
?
m
3
)
…
…
x
≡
a
r
(
m
o
d
?
m
r
)
x\equiv a_1(mod \ m_1)\\ x\equiv a_2(mod\ m_2)\\ x\equiv a_3(mod\ m_3)\\ \dots\\ \dots\\ x\equiv a_r(mod\ m_r)
x≡a1?(mod?m1?)x≡a2?(mod?m2?)x≡a3?(mod?m3?)……x≡ar?(mod?mr?)
有模
M
=
m
1
m
2
m
3
?
?
?
m
r
M=m_1m_2m_3*\dots*m_r
M=m1?m2?m3????mr????的唯一解,即为中国剩余定理。
求解思路:
- 令 M i = M / m i M_i=M/m_i Mi?=M/mi?由于 m i , m j m_i,m_j mi?,mj?互质,因此 g c d ( M i , m i ) = 1 gcd(M_i,m_i)=1 gcd(Mi?,mi?)=1,即 M i P i ≡ 1 ( m o d ? m i ) M_iP_i\equiv 1 (mod\ m_i) Mi?Pi?≡1(mod?mi?),满足扩展欧几里得的求解。
- r e s = a 1 M 1 P 1 + a 2 M 2 P 2 + ? + a r M r P r res=a_1M_1P_1+a_2M_2P_2+\dots+a_rM_rP_r res=a1?M1?P1?+a2?M2?P2?+?+ar?Mr?Pr????? ,res即为最小解
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll exgcd(ll a, ll b, ll &x, ll &y)
{
if(b==0)
{
x = 1, y = 0;
return a;
}
ll d = exgcd(b, a%b, y, x);
y -= a/b*x;
return d;
}
int main()
{
int n;
cin>>n;
vector<ll>A(n+1),B(n+1);
ll M=1ll,res=0;
for(int i=1;i<=n;i++)cin>>A[i]>>B[i],M*=A[i];
for(int i=1;i<=n;i++)
{
ll x, y;
exgcd(M/A[i], A[i], x, y);//求逆元
res = (res + B[i]*M/A[i]*x)%M;
}
cout<<(res+M)%M<<endl;
}
康托展开
康托展开问题:
给定一个长度为n的排列,问该排列在全排列中的位置,例如:
123 1
132 2
213 3
231 4
312 5
312 6
这是将全排列与整数相映射,形成双射函数。
核心思想:数位dp分叉思想,当前未在之前出现比当前位小的数不论之后如何排列,都要比该数小。
具体求解步骤:
- 预处理处阶乘数组
- 开始分叉处理,因为要知道有几个数未曾出现并且比当且数小,所以可以利用树状数组优化。
- 总时间复杂度 o ( n l o g n ) o(nlog_n) o(nlogn?)?
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=998244353;
const int maxn=1e6+5;
ll jc[maxn],c[maxn];
inline int lowbit(int x)//树状数组吧
{
return x&(-x);
}
inline void updata(int x,int y,int n)
{
for(int i=x;i<=n;i+=lowbit(i))c[i]+=y;
}
inline ll getsum(int x)
{
ll ans=0;for(int i=x;i>0;i-=lowbit(i))ans+=c[i];
return ans;
}
void pre_jc()//预处理阶乘
{
ll num=1;jc[0]=1;
for(ll i=1;i<maxn;i++)
{
num=(num*i)%mod;
jc[i]=num;
}
}
int main()
{
ios::sync_with_stdio(false);
pre_jc();
int n;
cin>>n;
for(int i=1;i<=n;i++)updata(i,1,n);
ll res=0;
for(int i=1;i<=n;i++)
{
int num;cin>>num;
getsum(num-1);
res=(res+getsum(num-1)*jc[n-i]%mod)%mod;//核心代码
updata(num,-1,n);
}
cout<<(res+1)%mod<<endl;//res是有多少比自己小,所以要加1
return 0;
}
Burnside 定理与Polya定理
给定一个n格的环,m涂色,有多少种本质不同的方案
一般可以证明:当只有旋转的时候(顺时针或逆时针),对于一个有n个字符的环,可顺时针或逆时针旋转几个位置,由于至少有n个置换,但是假设我顺时针旋转k个位置,他就等同于逆时针转动n-k个位置,假设一个置换为:G={π0,π1,π2,π3,π4,…,πn-1},这个时候可以证明逆时针旋转k个位置时πk的循环节的个数为Gcd(n,k),且每个循环的长度为L=n/gcd(n,i)。
Polya 定理得
a
n
s
w
e
r
=
∑
i
=
1
n
m
g
c
d
(
i
,
n
)
n
answer = \frac{\sum_{i=1}^{n}m^{gcd(i,n)}}{n}
answer=n∑i=1n?mgcd(i,n)?
组合数
当数据范围小于等于3000 30003000左右时,可直接根据组合数的一个性质:C ( n , m ) = C ( n ? 1 , m ) + C ( n ? 1 , m ? 1 ) 直接递推计算,时间复杂度为 O(n^2).
高精取模
int b[N],n; //高精度数,表示n
int ksm(int a,int m) {
int ans=1;
for(int i=0;i<n;++i) {
for(int j=0;j<b[i];++j) ans=1ll*ans*a%m;
int tmp=1;
for(int j=0;j<10;++j) tmp=1ll*tmp*a%m;
a=tmp;//乘十次
}
return ans;
}
筛法
1e6中有80000个素数
1.普通素数筛
时间复杂度n2
2.埃斯筛
时间复杂度(nloglog n)
3.欧拉筛
时间复杂度o(n)
int a[maxn],b[maxn],c[maxn],ans=0;
for(int i=2;i<maxn;i++)
{
if(a[i]==0)b[++ans]=i;
for(int j=1;i*b[j]<maxn&&j<=ans;j++)
{
a[i*b[j]]=1;c[i*b[j]]=c[i]+1;
if(i%b[j]==0)break;
}
}
4.min25筛
空间n^0.5 时间为(n^0.75/ln n +n/poly(ln n))一秒1e10;
//问题描述定义:
//定义sigma(n)为n的正因数的数量,求f(n,k)=sum_{i=1}^n (sigma(i^k))
#include<stdio.h>
#include<math.h>
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=200005;
int T,S,pr[N],pc;
ll n,num[N],m,K;
ull g[N];
bool fl[N];
// 给定一个数字X求出其为第几个可以得到有效的g的数字
inline int ID(ll x){return x<=S?x:m-n/x+1;}
ull f(ll n,int i){
if(n<1||pr[i]>n)return 0;
ull ret=g[ID(n)]-(i-1)*(K+1);
while((ll)pr[i]*pr[i]<=n){
int p=pr[i];
ull e=K+1,t=n/p;
while(t>=p)ret+=f(t,i+1)*e+e+K,t/=p,e+=K;
// ret= sum{sigma(p^es)([n>1]+f(n/p^es,p)+g[n]-g[num[i-1]]}
// 因为对于函数g(n,m)当n<=m^2,g(n,m)为0
// 且根据sigma函数的性质,对于质数p,有sigma(p^es)=es*k+1
// 所以 ret+=(es*k+1)*f(n/p^es,p)+((es+1)k+1)(1<=es&& n/p^es>p)即当前项的sigma(p^e)*f(n/p^e,p)加上下一项的sigma(p^e)
// 这样的做法避免了e<1也就不必进行特判
i++;
}
return ret;
}
//g[i]即小于i的所有质数的sigma函数求和
//根绝前面的推导,只有当i可以通过[n/m]得到时,其才有用
ull solve(ll n){
int i,p,x;ull y;
S=sqrt(n);
while((ll)S*S<=n)S++;
while((ll)S*S>n)S--;
while(m)num[m--]=0;
for(i=1;i<=S;i++)num[++m]=i;
for(i=S;i>=1;i--)if(n/i>S)num[++m]=n/i;
for(i=1;i<=m;i++)g[i]=num[i]-1;
//此处g[i]为小于等于第i个满足可以通过[n/m]得到的数的素因子的数量
//故先减去“1”因为1一定不为素因子且无法被后续操作筛去
x=1;y=0;
for(p=2;p<=S;p++)if(g[p]!=g[p-1]){
while(num[x]<(ll)p*p)x++;
//令g'(i,j)为埃氏筛法筛出前j个素数后,1到j之间剩余数的数量
//则有g'(i,j)=g'(0,j)-sum_{k=0,k<i}(g'(k,[j/p[k+1]])-g'(k,p[k]))
//其中p[0]=1,p[i](i>0)为第i个质数
//则g(j)即为g'(i,j)使得有p[i]<j&&p[i+1]>j
//其中g'(k,p[k])即为k+1
//由于以上的递推式仅仅作用到num[x]>=p^2为止,故仅仅将更新到x
//由于每次都要减去尚未去除当前素数的g以充当g'因此从大往小更新
for(i=m;i>=x;i--)g[i]-=g[ID(num[i]/p)]-y;
y++;
}
for(i=1;i<=m;i++)g[i]*=K+1;
return f(n,1)+1;
}
int main(){
int i,j;
//素数筛
for(i=2;i<N;i++)if(!fl[i]){
pr[++pc]=i;
for(j=i+i;j<N;j+=i)fl[j]=1;
}
for(scanf("%d",&T);T--;){
scanf("%lld%lld",&n,&K);
printf("%llu\n",solve(n));
}
return 0;
}
三分查找
#include<bits/stdc++.h>
using namespace std;
const int maxn=16;
const double eps=1e-7;
double a[maxn];
int n;
double f(double x)
{
double res=0,xx=1;
for(int i=0;i<=n;i++)
{
res+=a[i]*xx;xx*=x;
}
return res;
}
int main()
{
double l,r;
cin>>n>>l>>r;
for(int i=0;i<=n;i++)
{
cin>>a[n-i];
}
//for(int i=0;i<=n;i++)cout<<a[i]<<" ";cout<<endl;
while((r-l)>eps)
{
double midl=(r-l)/3+l,midr=r-(r-l)/3;
double ansl=f(midl),ansr=f(midr);
if(ansr>ansl)l=midl;
else if(ansl>ansr)r=midr;
else l=midl,r=midr;
}
//cout<<f(-4.1)<<" "<<f(-4.9)<<endl;
cout<<l<<endl;
return 0;
}
约瑟夫问题
首先,对于经典的约瑟夫环问题,我们记f(n,m)表示初始有n 个人,第m 个出队的人是谁(从0号开始报数)。则有递推式f(n,m)=(f(n?1,m?1)+k) % n 其中k表示每报数k次一个人出队,注意编号从0开始。
莫比乌斯反演
莫比乌斯反演实际上是一两个公式定理的运用,自认为想要掌握它的话,其中的证明还是有必要了解的。看过网上一些博客,感觉都只证明了一半,没看到有人将这个定理完全证明出来。然而我最近在正好在学习初等数论,发现完全证明这个定理实际上并不需要很多知识,特此填坑。
实际上,这个定理的证明用到了一点数论函数相关知识。前置技能在此
https://blog.csdn.net/tomandjake_/article/details/81083051
内容并不多,自认为把这一页笔记内容学会,自己就可以把莫比乌斯反演的证明当练习题一样独立完成。接下来我还是会解释,当然,如果觉得我的解释不好,完全可以自己看这个笔记学习,我甚至都推荐自己看笔记,因为如果熟悉这样的数学语言,其实看的很快而且会有自己的认识。而且其中给出了欧拉函数的推导,没有学过欧拉函数的话,看这个也可以更加高效地学完这一块内容。(注意笔记中(m,n)=gcd(m,n) )
好,进入正题。首先引入三个定义
Definition 1 可乘函数:算术函数f,满足 只要gcd(m,n) =1,就有f(mn)=f(m)f(n)。
没错, 比其他可乘函数宽泛一点,只要在gcd(m,n)=1条件下满足可乘就行。然后我们知道由唯一分解定理,任何正整数n可分解为若干素数的幂方积,所以若为可乘函数,有
Definition 2 : 代表对n的所有正因子求和,如
?
Definition 3 莫比乌斯函数:
?
定义有点奇怪,关于这个函数,之后我们可以看到它的作用, 必须提到的是,可以证明,莫比乌斯函数是可乘函数。
然后是我们的目标----莫比乌斯反演定理:
Theorem 1 莫比乌斯反演定理: F(n)和f(n)为算术函数,若他们满足
?
则有
?
证明如下:
首先给出一个定理,
已知为可乘函数。
之后可以得到下一个定理
定理3证明:
可以看到,莫比乌斯反演提供了一个F(n)与f(n)的连接,而他们之间的桥梁就是莫比乌斯函数。之后我们会看到具体的例子。这里先给出线性筛莫比乌斯函数的代码:
int mu[maxn], vis[maxn];
int primes[maxn], cnt;
void get_mu() {
memset(vis, 0, sizeof(vis));
memset(mu, 0, sizeof(mu));
cnt = 0; mu[1] = 1;
for (int i = 2; i <= maxn; ++i) {
if (!vis[i]) { primes[cnt++] = i; mu[i] = -1; }
for (int j = 0; j<cnt&&primes[j] * i <= maxn; ++j) {
vis[primes[j] * i] = 1;
if (i%primes[j] == 0)break;
mu[i*primes[j]] = -mu[i];
}
}
}
应用举例:POJ 3904
题目给出n和n个正整数,问能找出多少个不同的四元组(a,b,c,d)使得该四元组的最大公因数为1.
分析:
首先要提的是,我们做题目往往用的是莫比乌斯反演的另外一种形式:
既然要用到莫比乌斯反演,我们首先就要找到合适的F和f。实际上,F和f的关系在于整除。我们可以假设
F(n)为有多少个四元组满足gcd(a,b,c,d)=n的整数倍
f(n)为有多少个四元组满足gcd(a,b,c,d)=n
所以我们的目标就是求f(1), 而实际上可以看出F与f构成了一组莫比乌斯变换对。有了反演公式,我们可以通过求F来求f,而这里面F很好求,要求F(n)我们只要在原数组中数出到能被n整除的数的个数m, 则C(m,4)就是F(n)
而由公式,由此我们可以发现
直接计算即可。
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<vector>
#include<stack>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<sstream>
#include<cmath>
#include<iterator>
#include<bitset>
#include<stdio.h>
using namespace std;
#define _for(i,a,b) for(int i=(a);i<(b);++i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
typedef long long LL;
const int INF = 1 << 30;
const int MOD = 1e9 + 7;
const int maxn = 10005;
int n, a[maxn], tot[maxn];
int mu[maxn], vis[maxn];
int primes[maxn], cnt;
void get_mu() {
memset(vis, 0, sizeof(vis));
memset(mu, 0, sizeof(mu));
cnt = 0; mu[1] = 1;
for (int i = 2; i <= maxn; ++i) {
if (!vis[i]) { primes[cnt++] = i; mu[i] = -1; }
for (int j = 0; j<cnt&&primes[j] * i <= maxn; ++j) {
vis[primes[j] * i] = 1;
if (i%primes[j] == 0)break;
mu[i*primes[j]] = -mu[i];
}
}
}
void get_tot() {
memset(tot, 0, sizeof(tot));
for (int i = 0; i<n; ++i) {
int x = a[i];
int m = sqrt(x);
for (int j = 1; j <= m; ++j) {
if (x%j == 0)tot[j]++, tot[x / j]++;
}
if (m*m == x)tot[m]--;
}
}
LL Cn4(int m) {
if (m == 0)return 0;
return 1ll * m*(m - 1)*(m - 2)*(m - 3) / 24;
}
int main()
{
//freopen("C:\\Users\\admin\\Desktop\\in.txt", "r", stdin);
//freopen("C:\\Users\\admin\\Desktop\\out.txt", "w", stdout);
get_mu();
while (~scanf("%d", &n)) {
for (int i = 0; i<n; ++i) scanf("%d", &a[i]);
get_tot();
LL ans = 0;
for (int i = 1; i<maxn; ++i) {
ans += 1ll * mu[i] * Cn4(tot[i]);
}
printf("%I64d\n", ans);
}
return 0;
}
扩展欧几里德(求逆元)
//扩展欧几里德
int exgcd(int a,int b,long long &x,long long &y)
{
if(b==0)return x=1,y=0,a;
int d=exgcd(b,a%b,y,x);//d的值实际上就是gcd(a,b),如果不需要的话可以不求
return y-=a/b*x,d;
}
//利用扩展欧几德求逆元
long long inv(long long a,long long m)
{
long long x,y;
long long d=exgcd(a,m,x,y);
return d==1?(x+m)%m:-1;//不互质就没有逆元
}
博弈问题
0x00 公平组合游戏ICG
若一个游戏满足:
由两名玩家交替行动
在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关
游戏中的同一个状态不可能多次抵达(有向无环),游戏以玩家无法行动为结束,且游戏一定会在有限步后以非平局结束
则称该游戏为一个公平组合游戏。
例如 Nim 博弈属于公平组合游戏,而普通的棋类游戏,比如围棋,就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子,胜负判定也比较复杂,不满足条件2和条件3。
0x01 有向图游戏(博弈图)
给定一个有向无环图,图中有一个唯一的起点,在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是,把每个局面看成图中的一个节点,并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。 转化为有向图游戏,也称绘制了它的博弈状态图(简称博弈图或游戏图)。
这样,对于组合游戏中的每一次对弈(每一局游戏),我们都可以将其抽象成游戏图中的一条从某一顶点到出度为 0 的点的路径。
组合游戏向图的转化,并不单单只是为了寻找一种对应关系,它可以帮助我们淡化游戏的实际背景**,强化游戏的数学模型,更加突出游戏 的数学本质。**
0x02 先手必胜和先手必败
先手必胜状态 : 先手行动以后,可以让剩余的状态变成必败状态 留给对手(下一步是对手(后手)的局面)。
先手必败状态 : 不管怎么操作,都达不到必败状态,换句话说,如果无论怎么行动都只能达到一个先手必胜状态留给对手,那么对手(后手)必胜,先手必败。
简化一下就是:
先手必胜状态:可以走到某一个必败状态
先手必败状态:走不到任何一个必败状态
因为我们当前走到的状态是送给对手的状态h
通常先手是 Alice ,后手是Bob 。
定理:
定理 2.1: 没有后继状态的状态是必败状态。
定理 2.2: 一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。
定理 2.3: 一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。
如果博弈图是一个有向无环图,则通过这三个定理,我们可以在绘出博弈图的情况下用 O(N+M) 的时间(其中 N 为状态种数,M 为边数)得出每个状态是必胜状态还是必败状态。
0x03 必胜点和必败点
必败点(P点) 前一个(previous player)选手将取胜的点称为必败点
必胜点(N点) 下一个(next player)选手将取胜的点称为必胜点
(1) 所有终结点是必败点(P点)
(2) 从任何必胜点(N点)操作,至少有一种方法可以进入必败点(P点)
(3)无论如何操作, 从必败点(P点)都只能进入必胜点(N点)
0x04 有向图的核
给定一张DAG图<V,E>,如果 V 的一个点集 S 满足:
S 是独立集(集合内的点互不相通)
集合V?S 中的点都可以通过一步到达集合 S 中的点( V?S 指 S 在 V 中的补集)
则称 S 是图 V的一个核。
结论: 核内节点对应 SG 组合游戏的必败态
因为 Alice 当前的棋子在 S 中,由于 S 是独立集,也就意味着 Alice 只能将棋子从 S 移动到 V?S
而 Bob又可以通过一步移动将棋子从 V?S 移动到了 S,这样 Alice 就好像是被支配了一样,被迫把棋子移动到了没有出度的必败节点,Alice 必败,Bob必胜!
1.巴氏博弈:后手控制和先手的数量之和
2.威佐夫博弈:有两堆小石子,两个人轮流从某一堆里取石子或从两堆中取相同的石子,每次取石子的个数>=1.
int temp = (1.0 + sqrt(5) )/ 2 * (m - n);当差为奇艺局势时,先手必败;
3.尼姆博弈:有m堆小石子,两个人轮流从某堆里取石子,每次取石子的个数>=1.最后取光者得胜;
把每堆物品数全部异或起来,如果得到的值为0,那么先手必败,否则先手必胜。
4.斐波那契博弈:有一堆物品,两人轮流取物品,先手最少取一个,至多无上限,但不能把物品取完,
之后每次取的物品数不能超过上一次取的物品数的二倍且至少为一件,取走最后一件物品的人获胜。
结论是:先手胜当且仅当n不是斐波那契数(n为物品总数)
FFT 快速变换傅里叶
卷积 (Convolution)(Convolution) ,准确来说是一种通过两个函数 f 和g 生成第三个函数的一种数学算子.
从广义上定义:
? h(x)=∫∞?∞g(τ)?f(x?τ)dτ
在多项式域,那么就把其定义划进多项式,得到:
? [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E7C3PGsH-1636816370798)(file:///C:\Users\二月\AppData\Roaming\Tencent\Users\2211979172\QQ\WinTemp\RichOle\N[VN25XX49A19W$S_AI]L8F.png)]
其中 A(x)和 B(x)均为 n?1次多项式
比较显然的是,在我们合并同类项的情况下,最终卷出来的结果应该有 2n+1 项。
我们知道,原本的多项式是系数表示法,现在我们将其转化为点值表示法 (dot method)。即我们可以把多项式 F(x)转化为多项式函数 f(x) ,那么这个 n 阶函数就可以由 n+1 个点唯一确定。即给定
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cEIKs1Sc-1636816370806)(file:///C:\Users\二月\AppData\Roaming\Tencent\Users\2211979172\QQ\WinTemp\RichOle\P}X1}EMQG2ZQ6KA$}_9`K[J.png)]
对于一个多项式乘法问题,当给出系数表示法的时候, O(n^2)的复杂度有时候并不足够优越,而FFT就是一个能使多项式乘法做到O(nlogn)的一个算法,具体的原理其实非常清晰:
两个多项式的系数表示法求值,O(nlogn)
两个多项式的点值表示法点值乘法,O(n)
两个多项式乘积的点值表示法插值,O(nlogn)
两个多项式乘积的系数表示法
暴力算法(O(n^3))
要先做题,必先暴力
首先是求值,加入你现在随便找了n个互不相同的x,带入其中,是什么复杂度呢**O(n^2)**的然后是插值, 有一个非常妙的方法,假设所有的a都是未知数,那么这个问题就变成了经典的高斯消元问题,复杂度O(n^3)
不好意思,这两个操作的复杂度都光荣的在 O(n2)以上,使得当前这个算法的总复杂度为O(n3),比文章开始的那个O(n^2)都要差,不要灰心,既然复杂度不优,那就循序渐进的优化
离散傅里叶变换
点值表示法有一个很好的特性,就是那个代入的x可以自己选择
离散傅里叶变换的思路是将n个x的值取n个单位根(模长为一的复数)
复数(这是一个知识拓展框)
这个数,在实数范围内是不存在的,所以拓展出复数这一概念,设i = ? 1
,复数就是能够被表示为z = x + y ? i z=x+y*iz=x+y?i的数。所以对一个复数,可以用有序数对(x,y)表示,在坐标轴上有对应的点,而这个复数就是从(0,0)到(x,y)的一条有向线段(只会向量的同学可以把它看成向量),而这个复数的模长就等于(0,0)到(x,y)的距离
由于复数是数,所以也有各种运算
加法:(a+bi)+(c+di)=(a+c)+(b+d)i
减法:(a+bi)-(c+di)=(a-c)+(b-d)i
乘法:(a+bi)*(c+di)=(ac-bd)+(ad+bc)i
当然,C++有专门的complex变量可以声明,但是
不推荐使用!!!
为什么呢?因为FFT本身就有一定的常数,如果再用系统complex常数会更大,所以推荐自己手写struct
二进制常数优化后的FFT
#include<cstdio>
#include<cctype>
#include<cmath>
namespace fast_IO
{
const int IN_LEN=10000000,OUT_LEN=10000000;
char ibuf[IN_LEN],obuf[OUT_LEN],*ih=ibuf+IN_LEN,*oh=obuf,*lastin=ibuf+IN_LEN,*lastout=obuf+OUT_LEN-1;
inline char getchar_(){return (ih==lastin)&&(lastin=(ih=ibuf)+fread(ibuf,1,IN_LEN,stdin),ih==lastin)?EOF:*ih++;}
inline void putchar_(const char x){if(oh==lastout)fwrite(obuf,1,oh-obuf,stdout),oh=obuf;*oh++=x;}
inline void flush(){fwrite(obuf,1,oh-obuf,stdout);}
}
using namespace fast_IO;
#define getchar() getchar_()
#define putchar(x) putchar_((x))
typedef long long LL;
#define rg register
#define complex Complex //防止和库函数冲突
template <typename T> inline void swap(T&a,T&b){T c=a;a=b;b=c;}
template <typename T> inline void read(T&x)
{
char cu=getchar();x=0;bool fla=0;
while(!isdigit(cu)){if(cu=='-')fla=1;cu=getchar();}
while(isdigit(cu))x=x*10+cu-'0',cu=getchar();
if(fla)x=-x;
}
template <typename T> void printe(const T x)
{
if(x>=10)printe(x/10);
putchar(x%10+'0');
}
template <typename T> inline void print(const T x)
{
if(x<0)putchar('-'),printe(-x);
else printe(x);
}
const int maxn=2097153;const double PI=acos(-1.0);
int n,m;
struct complex
{
double x,y;
inline complex operator +(const complex b)const{return (complex){x+b.x,y+b.y};}
inline complex operator -(const complex b)const{return (complex){x-b.x,y-b.y};}
inline complex operator *(const complex b)const{return (complex){x*b.x-y*b.y,x*b.y+y*b.x};}
}a[maxn],b[maxn];
int lenth=1,Reverse[maxn];
inline void init(const int x)
{
rg int tim=0;
while(lenth<=x)lenth<<=1,tim++;
for(rg int i=0;i<lenth;i++)Reverse[i]=(Reverse[i>>1]>>1)|((i&1)<<(tim-1));
}
inline void FFT(complex*A,const int fla)
{
for(rg int i=0;i<lenth;i++)if(i<Reverse[i])swap(A[i],A[Reverse[i]]);
for(rg int i=1;i<lenth;i<<=1)
{
const complex w=(complex){cos(PI/i),fla*sin(PI/i)};
for(rg int j=0;j<lenth;j+=(i<<1))
{
complex kk=(complex){1,0};
for(rg int k=0;k<i;k++,kk=kk*w)
{
const complex x=A[j+k],y=A[j+k+i]*kk;
A[j+k]=x+y;
A[j+k+i]=x-y;
}
}
}
}
int main()
{
read(n),read(m);
init(n+m);
for(rg int i=0;i<=n;i++)read(a[i].x);//读入多项式A(n+1)项
for(rg int i=0;i<=m;i++)read(b[i].x);//读入多项式B(m+1)项
FFT(a,1),FFT(b,1);//对多项式求点值
for(rg int i=0;i<lenth;i++)a[i]=a[i]*b[i];//点值相乘
FFT(a,-1);//对多项式求插值
for(rg int i=0;i<=n+m;i++)print((int)(a[i].x/lenth+0.5)),putchar(' ');//lenth看上面,就分治之类的
return flush(),0;
}
/*
1 2
1 2
1 2 1
1 4 5 2
*/
高斯消元法
高斯消元解线性方程组
步骤:
- 增广矩阵行初等行变换为行最简形;
- 还原线性方程组;
- 求解第一个变量;
- 补充自由未知量;
- 列表示方程组通解。
const int N = 507, mod = 1e9 + 7;
const double eps = 1e-6;
int n, m;
double a[N][N];
int guass()
{
int c;//当前最左边的一列
int r;//当前最上面的一行
for(c = 1, r = 1; c <= n; ++ c){
int t = r;
for(int i = r + 1; i <= n; ++ i){
if(fabs(a[i][c]) > fabs(a[t][c]))
t = i;
}
if(fabs(a[t][c]) < eps)//等于0就下一个
continue;
//换到第一行(最上面的一行)
for(int i = c; i <= n + 1; ++ i)
swap(a[t][i], a[r][i]);
//把该行第一个数变成 1(该行每一列都/=第c列的值)
for(int i = n + 1; i >= c; -- i)
a[r][i] /= a[r][c];
//中间所有列(所有项)全部消掉
for(int i = r + 1; i <= n; ++ i)
if(fabs(a[i][c]) > eps)
for(int j = n + 1; j >= c; -- j)
a[i][j] -= a[r][j] * a[i][c];
r ++ ;
}
if(r <= n){
for(int i = r; i <= n; ++ i)
if(fabs(a[i][n + 1]) > eps)//非零,无解
return 2;
return 1;//无穷多组解
}//回代
//行最简形矩阵
for(int i = n; i >= 1; -- i)
for(int j = i + 1; j <= n + 1; ++ j)
a[i][n + 1] -= a[j][n + 1] * a[i][j];
/* 只要保留第i行第i列的系数即可,所以从第i+1行开始一直消到第n行,
因为只要结果,所以可以只消第i行第n+1列的数(b);就是上面消掉所有列的简化版,少了一个for循环*/
return 0;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; ++ i)
for(int j = 1; j <= n + 1; ++ j)
cin >> a[i][j];
int t = guass();
if(t == 0){
for(int i = 1; i <= n; ++ i)
printf("%.2f\n", a[i][n + 1]);
}
else if(t == 1)puts("Infinite group solutions");//无穷组解
else puts("No solution");//无解
return 0;
}
高斯-约旦消元法
约旦消元法的精度更好、代码更简单,没有回带的过程。
约旦消元法大致思路如下:
- 1.选择一个尚未被选过的未知数作为主元,选择一个包含这个主元的方程。
- 2.将这个方程主元的系数化为1。
- 3.通过加减消元,消掉其它所有方程中的这个未知数。
- 4.重复以上步骤,直到把每一行都变成只有一项有系数。
我们用矩阵表示每一项系数以及结果.
有被出题人卡的风险。
const int N = 5007;
const double eps = 1e-6;//
int n, m;
double a[N][N];
int guass() {
for(int i = 1; i <= n; ++ i) {//枚举列
int maxx = i;
//1.找
for(int j = i + 1; j <= n; ++ j)
//第i列以前的未知量除了第i一行的所有行都已经都已经消成0了,不能再动了
if(fabs(a[j][i]) > fabs(a[maxx][i]))
maxx = j;
//2.换
for(int j = 1; j <= n + 1; ++ j)//找到的最大一行跟第i行换
swap(a[i][j], a[maxx][j]);
if(fabs(a[i][i]) < eps) return -1;
//3.减
for(int j = 1; j <= n; ++ j)
//把该未知量除第i行以外全部减成0(普通的高斯是第i行以下减为0,但是需要回代)
if(j != i) {
double tmp = a[j][i] / a[i][i];
for(int k = i + 1; k <= n +1; ++ k) //只需要减第i列右边就行了,因为左边全为0
a[j][k] -= a[i][k] * tmp;
} //高斯 - 约旦 消元法
} //最后会得到这样的矩阵
for(int i = 1; i <= n; ++ i) // k1*a=e1
a[i][n + 1] /= a[i][i]; // k2*b=e2
//所以最后要除以该项的系数 <-- // k3*c=e3
return 1; // k4*d=e4
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; ++ i)
for(int j = 1; j <= n + 1; ++ j)
scanf("%lf", &a[i][j]);
int ans = guass();
if(ans == -1) puts("No Solution");
else for(int i = 1; i <= n; ++ i)
printf("%.2f\n", a[i][n + 1]);
return 0;
}
高斯消元解亦或线性方程组
输入一个包含n个方程n个未知数的异或线性方程组。
方程组中的系数和常数为0或1,每个未知数的取值也为0或1。
求解这个方程组。
异或线性方程组示例如下:
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
const int N = 107, M = 500007, INF = 0x3f3f3f3f;
int n, m;
bitset<120> a[N];
int guass(int n, int m)//n row n 行 m col m 列
{
int row = 0, col = 0, maxx;
for(; col < m; ++ col) {
for(maxx = row; maxx < n; ++ maxx)
if(a[maxx][col])
break;
if(maxx == n) continue;
if(a[maxx][col] == 0) continue;
swap(a[maxx], a[row]);
for(int i = row + 1; i < n; ++ i)
if(a[i][col]) //如果这一列有数的话那一行全部消掉
a[i] = a[i] ^ a[row];
//for(int j = n; j >= col; -- j)//col前面都是0,无所谓
//a[i][j] = a[i][j] ^ a[row][j];
row ++ ;
}
if(row < n) {
for(int i = row; i < n; ++ i)
if(a[i][m])//矛盾,出现非零的常数项等于0,说明无解
return 2;
return 1;//有无穷多组解
}
//行最简形矩阵,第i行第i列的表示的未知量x_i的一个解
for(int i = n - 1; i >= 0; -- i) {//第i行,第i行第i列
for(int j = i + 1; j < m; ++ j)//第j列,右边所有列都要消
a[i][m] = a[i][m] ^ (a[j][m] * a[i][j]);
}
return 0;
}
int x;
itn main()
{
scanf("%d", &n);
m = n;
for(int i = 0; i < n; ++ i)
for(int j = 0; j < m + 1; ++ j) //+1是因为多了一个常数矩阵(也即是答案)
scanf("%d", &x), a[i][j] = x;
int res = guass(n, m);
if(res == 0) {
for(int i = 0; i < n; ++ i)
x = a[i][m], printf("%d\n", x);
}
else if(res == 2) puts("No solution");
else puts("Multiple sets of solutions");
return 0;
}
拉格朗日插值法
图论
树的性质
树的直径
树上最远两点(叶子结点)的距离。
求法:从任意一点dfs(bfs)找到最长的点new,从new出发再dfs(bfs)再找最远的点last,new到last即为树的直径。
延伸:树上任意点能到的最远点,一定是树的直径的某个端点。
y总的有趣解法:自下而上看到达该点的最长路和次长路,两者相加即为最长路,缺点不好找这条路的左右端点。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
#define ll long long
vector<pair<int,ll> >a[maxn];
ll dis=-1e9;
ll dfs(int s, int fa)
{
ll d1=0,d2=0,d=0;
for(int i=0;i<a[s].size();i++)
{
int to=a[s][i].first;ll w=a[s][i].second;
if(to==fa)continue;
ll d=dfs(to,s);
if(d+w>=d1)d2=d1,d1=d+w;
else if(d+w>=d2)d2=d+w;
}
dis=max(d1+d2,dis);
return d1;
}
int main()
{
ios::sync_with_stdio(false);
int n;
cin>>n;
for(int i=1;i<n;i++)
{
int u,v;ll w;
cin>>u>>v>>w;
a[u].push_back({v,w});
a[v].push_back({u,w});
}
dfs(1,0);
cout<<dis<<endl;
return 0;
}
树的中心
找到树上的一个点满足:该点到其他点的最远距离最小。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
#define ll long long
vector<pair<int, ll>> e[maxn];
ll d1[maxn], d2[maxn], up[maxn], prm1[maxn], prm2[maxn];
ll dfs(int s, int fa)
{
for (int i = 0; i < e[s].size(); i++)
{
int to = e[s][i].first;
ll w = e[s][i].second;
if (to == fa)
continue;
ll d = dfs(to, s);
if (d + w >= d1[s])
d2[s] = d1[s], d1[s] = d + w, prm2[s] = prm1[s], prm1[s] = to;
else if (d + w >= d2[s])
d2[s] = d + w, prm2[s] = to;
}
return d1[s];
}
void dfs2(int s, int fa)
{
for (int i = 0; i < e[s].size(); i++)
{
int to = e[s][i].first;
ll w = e[s][i].second;
if (to == fa)
continue;
if (prm1[s] != to)
up[to] = max(up[s], d1[s])+w;//如果s中的最長路包含to,那麼為d2+w,否則答案為d1+w;
else
up[to] = max(up[s], d2[s])+w;
dfs2(to, s);
}
}
int main()
{
ios::sync_with_stdio(false);
//freopen("1.txt","r",stdin);
int n;
cin >> n;
for (int i = 1; i < n; i++)
{
int u, v;
ll w;
cin >> u >> v >> w;
e[u].push_back({v, w});
e[v].push_back({u, w});
}
dfs(1, -1);
//for(int i=1;i<=n;i++)cout<<d1[i]<<endl;
dfs2(1, -1);
ll res = 1e9 + 1;
for (int i = 1; i <= n; i++)
res = min(res, max(up[i], d1[i]));
cout << res << endl;
return 0;
}
/*
5
2 1 1
3 2 1
4 3 1
5 1 1
2
*/
dfs序
记录dfs时出栈和进栈的时间,通过记录下dfs序可以将其转换为dfs序,再利用各种数据结构来进行区间操作。
dfs获得dfs序
int r[maxn],c[maxn];
void dfs(int s,int fa)
{
r[s]=++dfn;
for(aotu it: v)
{
if()
}
c[s]=dfn;
}
性质:
判断两点是否在同一个根->叶上,即两点的区间是否有交集。
- 任意子树都是连续的。例如假设有个子树BEFKBEFK,在序列中对应的部分是:BEEFKKFBBEEFKKFB;子树CGHICGHI,在序列中对应的部分是:CGGHHIICCGGHHIIC。
- 任意点对(a,b)(a,b)之间的路径,可分为两种情况,首先是令lcalca是a、ba、b的最近公共祖先:
1.若lcalca是a、ba、b之一,则a、ba、b之间的inin时刻的区间或者outout时刻区间就是其路径。例如AKAK之间的路径就对应区间ABEEFKABEEFK或者KFBCGGHHIICAKFBCGGHHIICA。
2.若lcalca另有其人,则a、ba、b之间的路径为In[a]、Out[b]In[a]、Out[b]之间的区间或者In[b]、Out[a]In[b]、Out[a]之间的区间。另外,还需额外加上lcalca!!!考虑EKEK路径,对应为EFKEFK再加上BB。考虑EHEH之间的路径,对应为EFKKFBCGGHEFKKFBCGGH再加上AA。
LCA
最小生成树
1.prim法
时间o(n2);?
/*
*邮箱:unique_powerhouse@qq.com
*blog:https://me.csdn.net/hzf0701
*注:文章若有任何问题请私信我或评论区留言,谢谢支持。
*
*/
#include<bits/stdc++.h> //POJ不支持
#define rep(i,a,n) for (int i=a;i<=n;i++)//i为循环变量,a为初始值,n为界限值,递增
#define per(i,a,n) for (int i=a;i>=n;i--)//i为循环变量, a为初始值,n为界限值,递减。
#define pb push_back
#define IOS ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
#define fi first
#define se second
#define mp make_pair
using namespace std;
const int inf = 0x3f3f3f3f;//无穷大
const int maxn = 1e3;//最大值。
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> pll;
typedef pair<int, int> pii;
//*******************************分割线,以上为自定义代码模板***************************************//
int n,m;//图的大小和边数。
int graph[maxn][maxn];//图
int lowcost[maxn],closest[maxn];//lowcost[i]表示i到距离集合最近的距离,closest[i]表示i与之相连边的顶点序号。
int sum;//计算最小生成树的权值总和。
void Prim(int s){
//初始化操作,获取基本信息。
for(int i=1;i<=n;i++){
if(i==s)
lowcost[i]=0;
else
lowcost[i]=graph[s][i];
closest[i]=s;
}
int minn,pos;//距离集合最近的边,pos代表该点的终边下标。
sum=0;
for(int i=1;i<=n;i++){
minn=inf;
for(int j=1;j<=n;j++){
//找出距离点集合最近的边。
if(lowcost[j]!=0&&lowcost[j]<minn){
minn=lowcost[j];
pos=j;
}
}
if(minn==inf)break;//说明没有找到。
sum+=minn;//计算最小生成树的权值之和。
lowcost[pos]=0;//加入点集合。
for(int j=1;j<=n;j++){
//由于点集合中加入了新的点,我们要去更新。
if(lowcost[j]!=0&&graph[pos][j]<lowcost[j]){
lowcost[j]=graph[pos][j];
closest[j]=pos;//改变与顶点j相连的顶点序号。
}
}
}
cout<<sum<<endl;//closest数组就是我们要的最小生成树。它代表的就是边。
}
void print(int s){
//打印最小生成树。
int temp;
for(int i=1;i<=n;i++){
//等于s自然不算,故除去这个为n-1条边。
if(i!=s){
temp=closest[i];
cout<<temp<<"->"<<i<<"边权值为:"<<graph[temp][i]<<endl;
}
}
}
int main(){
//freopen("in.txt", "r", stdin);//提交的时候要注释掉
IOS;
while(cin>>n>>m){
memset(graph,inf,sizeof(graph));//初始化。
int u,v,w;//临时变量。
for(int i=1;i<=m;i++){
cin>>u>>v>>w;
//视情况而论,我这里以无向图为例。
graph[u][v]=graph[v][u]=w;
}
//任取根结点,我这里默认取1.
Prim(1);
print(1);//打印最小生成树。
}
return 0;
}
最短路
Dijkstra、Bellman_Ford、SPFA、Floyd
Dijkstra:适用于权值为非负的图的(单源最短路径),用斐波那契堆的复杂度O(E+VlgV),其实就是spfa加优先队列,保证每次出队的一定是全局最优解;
BellmanFord:适用于权值有负值的图的单源最短路径,并且能够检测负圈,复杂度O(VE)
SPFA:适用于权值有负值,且没有负圈的图的单源最短路径,论文中的复杂度O(kE),k为每个节点进入Queue的次数,
且k一般<=2,但此处的复杂度证明是有问题的,其实SPFA的最坏情况应该是O(VE).
Floyd:每对节点之间的最短路径
正权图使用dijkstra算法,负权图使用SPFA算法
SPFA算法:
时间复杂度
核心思想:利用队列,判断dp[当前点]和dp[上一个结点]+w的大小,如果更新了,就让其入队,visit[]看其是否在队列中,在就不用入队了。
判断有无负环:如果某个点进入队列的次数超过V次则存在负环(SPFA无法处理带负环的图)。
在没有负环、单纯求最短路径,不建议使用SPFA算法,而是用Dijkstra算法。
dijkstra算法:利用优先队列来保证每次更新最优,即出队之后便不用在出队
Bellman-ford算法:适用于单源最短路径,时间复杂度是O(VE)
dist[]:从original到其他顶点的最短路径长初始为无穷大,自然地,从original到original的距离为0。代表从original到各个顶点的最短路径长度。
pre[]:代表该点在最短路径中的上一个顶点。
1.初始化:除了起点的距离为0外(dist[original] = 0),其他均设为无穷大。
2.迭代求解:循环对边集合E的每条边进行松弛操作,使得顶点集合V中的每个顶点v的距离长逐步逼近最终等于其最短距离长;
3.验证是否负权环:再对每条边进行松弛操作。如果还能有一条边能进行松弛,那么就返回False,否则算法返回True
通过对每一条边松弛,迭代n次,时间复杂度O(VE),看起来有很大的优化空间,可以利用队列优化,优化之后就是赤裸裸的spafa;
floyd算法:
0x7fffffff:int 的最大值
spfa:
#include<iostream>
#include<string.h>
#include<stdio.h>
#include<queue>
#include<cmath>
#define ll long long
#define scf(x) scanf("%lld",&x)
using namespace std;
const int maxn=1e4+4;
const int maxm=5e5+5;
ll head[maxn],dp[maxn];
bool ex[maxn],dd[maxn];//前者是是否在对列中,后者是是否达到过
struct dt
{
ll v;
ll w;
ll next;
}p[maxm];
void zt(ll i,ll u,ll v,ll w){
p[i].w=w;
p[i].v=v;
p[i].next=head[u];
head[u]=i;
}
void spfa(ll s)
{
queue<ll>q;
q.push(s);
ex[s]=true;
dd[s]=true;
while(q.empty()==0)
{
ll n;
dp[s]=0;
n=q.front();
q.pop();
ex[n]=false;
for(ll i=head[n];i;i=p[i].next)
{
if(dp[p[i].v]>dp[n]+p[i].w)
{
dp[p[i].v]=dp[n]+p[i].w;
if(ex[p[i].v]==false)ex[p[i].v]=true,q.push(p[i].v);
}
dd[p[i].v]
=true;
}
}
}
int main()
{
memset(head,0,sizeof(head));
memset(ex,false,sizeof(ex));
memset(dp,0x3f,sizeof(dp));
memset(dd,false,sizeof(dd));
ll n,m,k,u,v,w,s;
cin>>n>>m>>s;
for(ll i=1;i<=m;i++)
{
scf(u);scf(v);scf(w);
zt(i,u,v,w);
}
spfa(s);
for(int i=1;i<=n;i++)
{
if(dd[i])printf("%lld ",dp[i]);
else printf("2147483647 ");
}
/* int sum=1;
for(int i=1;i<=31;i++)sum*=2;
sum-=1;
printf("%d",sum);*/
return 0;
}
dikjstra
朴素版:
朴素版的djstra的时间复杂度是个稳定的(n^2);
#include<bits/stdc++.h>
#define ll long long
using namespace std;
#define ll long long
const int maxn=1e3+3;
const int maxm=1e5+5;
const ll inf=0x7f7f7f;
ll dis[maxn],n,vis[maxn],S;
ll t[maxn][maxn];//利用邻接矩阵存图
void dijkstra()
{
memset(vis,0,sizeof(vis));//初始化标记数组
for(int i=1;i<=n;i++)
{
dis[i]=t[S][i];//更新从起点能到达的点的距离信息
}
dis[S]=0;//起点到起点距离为0;
vis[S]=1;int to;
for(int i=1;i<=n;i++)//找到最小的点作为新的起点
{
ll minn=inf+1;
for(int j=1;j<=n;j++)
{
if(minn>dis[j]&&!vis[j])
{
minn=dis[j];to=j;
}
}
// cout<<"find: "<<to<<" "<<dis[to]<<endl;
vis[to]=1;//将起点加入到已经更新的数组中
for(int j=1;j<=n;j++)
{
if(!vis[j])dis[j]=min(dis[j],dis[to]+t[to][j]);//更新dis数组
}
}
}
int main()
{
ios::sync_with_stdio(false);
int m;
cin>>n>>m>>S;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)t[i][j]=inf;//初始化图
for(int i=1;i<=m;i++)
{
int u,v;ll w;
cin>>u>>v>>w;
t[u][v]=w;
}
dijkstra();
for(int i=1;i<=n;i++)cout<<dis[i]<<" ";
return 0;
}
djkjstra+堆优化
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+5;
const int maxm=2e5+5;
struct edge
{
int to,next;
ll w;
}e[maxm*2];
int head[maxn],cnt=0,S;
ll vis[maxn],dis[maxn];int n;
void add(int s,int to,ll w)
{
e[++cnt].w=w;
e[cnt].to=to;
e[cnt].next=head[s];
head[s]=cnt;
}
struct node
{
int pos;ll dis;
bool operator <(const struct node &b)const
{
return dis>b.dis;
}
};
priority_queue<node>q;
void djk()
{
for(int i=1;i<=n;i++)dis[i]=1e17;//dis的初始化
dis[S]=0;
q.push({S,0});
while(!q.empty())
{
int s=q.top().pos;q.pop();//经过堆优化的也要像spfa一样。
if(vis[s]==1)continue;vis[s]=1;
for(int i=head[s];i;i=e[i].next)
{
int to=e[i].to;
if(dis[to]>e[i].w+dis[s])
{
dis[to]=e[i].w+dis[s];
if(vis[to]==0)q.push({to,dis[to]});
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
int m;
cin>>n>>m>>S;
for(int i=1;i<=m;i++)
{
int u,v;ll w;
cin>>u>>v>>w;
add(u,v,w);
}
djk();
for(int i=1;i<=n;i++)cout<<dis[i]<<" ";cout<<endl;
return 0;
}
dijkstra+势能优化
差分约数
-
求不等式组的可行解
源点需要满足的条件:从原点出发,一定可以遍历到所有的边。
步骤:
-
先将每个不等式 x i < = x j + c k x_i<=x_j+c_k xi?<=xj?+ck?,转化为一条从 x j x_j xj?走到 x i x_i xi?,长度为 c k c_k ck?的一条边
-
找到一个超级源点,使得该源点一定可以遍历到所有边
-
从源点求一遍单源最短路
结果1:如果存在负环,则原不等式组一定无解
结果2:如果没有负环,则 d i s t [ i ] dist[i] dist[i],就是原不等式组的一个可行解
-
-
如何求最大值或最小值
结论:如果求的是最小值,则应该求最长路;如果求的是最大值,则应该求最短路。
问题:如何转化 x i < = c x_i<=c xi?<=c,其中c是一个常数,这类的不等式
方法:建立一个超级源点,0,然后建立0->i , 长度是c的边即可。
以求 x i x_i xi?的最大值为例:求所有从 x i x_i xi?出发,构成的不等式链 x i < = x j + c 1 < = x k + c 2 + c 1 < = . . < = c 1 + c 2 + . . + c k x_i<=x_j+c_1<=x_k+c_2+c_1<=..<=c_1+c_2+..+c_k xi?<=xj?+c1?<=xk?+c2?+c1?<=..<=c1?+c2?+..+ck?? 所计算出的上界,最终 x i x_i xi?的最大值等于所有上界的最小值。
寻找强连通分量
tarjon算法
- 求取无向图的强连通分量只需要增加不回头的操作。
#include<stdio.h>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
const int maxn=+1e5+1e4+4;
const int maxm=1e5+1e4+5;
int n,m,ans,head[maxn],stack[maxn],top=0,visi[maxn],dfn[maxn],timer=0,low[maxn];ll f[maxn];
int color[maxn],cnt=0;
int u[maxm],v[maxn];
ll quan[maxn],nquan[maxn];ll res=0;
struct edge
{
int to,next;
}e[maxm];
inline void add(int s,int to)
{
e[++ans].to=to;
e[ans].next=head[s];
head[s]=ans;
}
void dfs(int s)//tarjon算法获得强连通分量
{
stack[++top]=s;visi[s]=1;
dfn[s]=low[s]=++timer;
for(int i=head[s];i;i=e[i].next)
{
if(dfn[e[i].to]==0)
{
dfs(e[i].to);
low[s]=min(low[s],low[e[i].to]);
}
else if(visi[e[i].to]==1)low[s]=min(low[s],dfn[e[i].to]);
}
if(low[s]==dfn[s])
{ cnt++;
color[s]=cnt;nquan[cnt]+=quan[s];visi[s]=0;//忘记变0,qwq!!!!
while(stack[top]!=s)
{
color[stack[top]]=cnt;
visi[stack[top]]=0;
nquan[cnt]+=quan[stack[top]];
top--;
}
top--;
}
}
void tp(int s)//记忆化搜索 ,不用按度入队
{
// cout<<s<<endl;
ll maxsum=0;
if(f[s]!=0)return ;
f[s]=nquan[s];
for(int i=head[s];i;i=e[i].next)
{
if(f[s]==0)tp(e[i].to);
maxsum=max(maxsum,f[e[i].to]);
}
f[s]+=maxsum;
}
inline int read(){
int x=0,ff=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')ff=-1; ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48; ch=getchar();}
return ff*x;
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)cin>>quan[i];
for(int i=1;i<=m;i++)
{
u[i]=read();v[i]=read();
add(u[i],v[i]);
}
for(int i=1;i<=n;i++)if(dfn[i]==0)dfs(i);
for(int i=1;i<=n;i++)head[i]=0;ans=0;
for(int i=1;i<=m;i++)e[i].next=0,e[i].to=0;
for(int i=1;i<=m;i++)
{
int uu=color[u[i]],vv=color[v[i]];
if(uu!=vv)//建立一张新图 ,如果两点不在同一个强连通分量就连边
{
add(uu,vv);
}
}
ll result=0;
for(int i=1;i<=cnt;i++)
{
if(f[i]==0)tp(i);
result=max(result,f[i]);
}
cout<<result<<endl;
return 0;
}
割点
在给定的一张无向图上,删去某个点能够使得图不连通,该点便被称为割点,对一张图进行dfs,当访问到u节点时,图上所有的点就被分成了两个部分,一部分是已经访问过的,另一部分是未被访问过的,假如在未被访问的点中有一个点是只能由u点访问的,那么点U便被称为割点。
二分图
二分图、不存在奇数环、染色不存在矛盾
匈牙利算法,匹配、最大匹配、匹配点、增广路径
最小点覆盖、最大独立集、最小路径覆盖(最小路径重复点覆盖)
最大匹配数 = 最小点覆盖=总点数-最大独立集=总点数-最小路径覆盖
最优匹配,KM(最小费用流)
多重匹配(最大流)
匈牙利算法
二分图
二分图匹配:将点分为两个集合,每个集合之中的点没有相连的两点
最大匹配:匹配边最多的边
匈牙利算法是用来求二分图的最大匹配的,它的核心问题就是找增广路径。匈牙利算法的时间复杂度为O(VE)
#include<bits/stdc++.h>
using namespace std;
const int maxn=510;
int line[maxn][maxn],used[maxn],nxt[maxn],n,m;
bool find(int x)
{
for(int i=1;i<=m;i++)
{
if(line[x][i]==1&&used[i]==0)
{
used[i] = 1;//cout<<i<<" "<<nxt[i]<<endl;
if(nxt[i] == 0||find(nxt[i]))//如果这个女生没有被匹配,或者这个女生匹配的男生能够被找到另外的女生匹配。
{
nxt[i] = x;
return true;
}
}
}
return false;
}
int match()
{
int sum=0;
for(int i=1;i<=n;i++)
{
memset(used,0,sizeof(used));//需要对女生清空
if(find(i))sum++;
}
return sum;
}
int main()
{
ios::sync_with_stdio(false);
int u,v,s;
cin>>n>>m>>s;
memset(nxt,0,sizeof(nxt));
memset(line,0,sizeof(line));
for(int i=1;i<=s;i++){
cin>>u>>v;
line[u][v]=1;}
int res=match();
cout<<res<<endl;
return 0;
}
网络流
Dicnic算法
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=205;//注意范围
const int maxm=5e3+5;
ll n,m,S,T;
ll head[maxn],rad[maxn],dis[maxn],cnt=1;
struct edge
{
int to,next;
ll w;
}e[maxm*2];
void add(int s,int to,ll w)
{
e[++cnt].to=to;
e[cnt].w=w;
e[cnt].next=head[s];
head[s]=cnt;
}
bool bfs()
{
memset(dis,0,sizeof(dis));
queue<ll>q;dis[S]=1;q.push(S);
while(!q.empty())
{
ll u=q.front();q.pop();rad[u]=head[u];
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(dis[v]==0&&e[i].w!=0)dis[v]=dis[u]+1,q.push(v);
}
}
return dis[T];
}
ll dfs(int now,ll rem)
{
if(now==T)return rem;
ll tem=rem;
for(int i=rad[now];i;i=e[i].next)
{
int v=e[i].to;rad[now]=i;
if(dis[v]==dis[now]+1&&e[i].w!=0)
{
ll k=min(e[i].w,tem);
ll dlt=dfs(v,k);
e[i].w-=dlt;e[i^1].w+=dlt;
tem-=dlt;
if(!tem)break;//加速,无残量结束
}
}
return rem-tem;
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++)
{
int u,v;ll w;
cin>>u>>v>>w;
add(u,v,w);
add(v,u,0);
}
ll res=0;
while(bfs())res+=dfs(s,1e18);
cout<<res<<endl;
return 0;
}
最小割求最大权闭合子图
最大权闭合子图
定义:
有一个有向图,每一个点都有一个权值(可以为正或负或0),选择一个权值和最大的子图,使得每个点的后继都在子图里面,这个子图就叫最大权闭合子图。
解法:该问题可以被转化为最小割问题
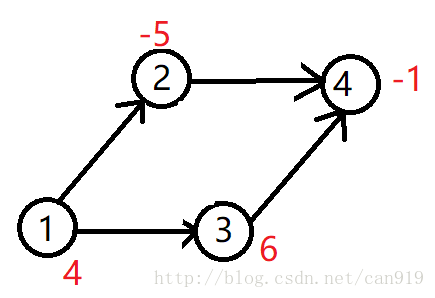
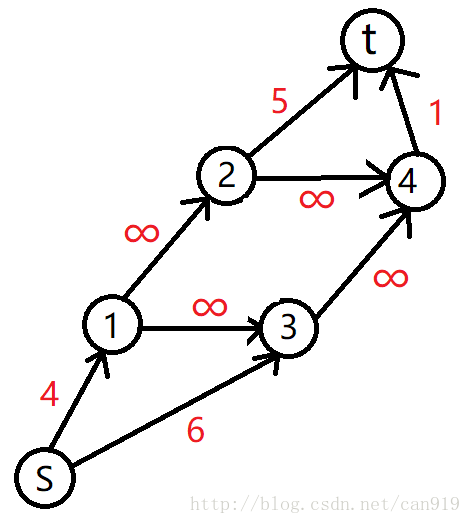
从源点s向每个正权点连一条容量为权值的边,每个负权点向汇点t连一条容量为权值的绝对值的边,有向图原来的边容量全部为无限大。
最大权闭合子图权值 = 所有权值为正的权值之和 - 最大流(最小割)
模糊的理解:
想要的是从s流出的边权,假如流量成功流入汇点,说明流量一定经过了副边,那么就需要减去副边。
对于该图,从S出发被割去的点即为不选的正权,流入T被割去的几位要选的反边。
方案输出:由上可知应当选所有与源点相连的点。
二分图互斥选点
经典题目:方格取数
最小割模型
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=1e4+4;
const int maxm=4e5+4;
ll a[105][105];
struct node
{
int to,next;
ll w;
}e[maxm*2];
int S,T,n,m,head[maxn],dis[maxn],rad[maxn],cnt=1;
void add(int s,int to,ll w)
{
e[++cnt].to=to;e[cnt].w=w;e[cnt].next=head[s];head[s]=cnt;
e[++cnt].to=s;e[cnt].w=0;e[cnt].next=head[to];head[to]=cnt;
}
bool bfs()
{
memset(dis,0,sizeof(dis));
queue<ll>q;q.push(S);dis[S]=1;
while(!q.empty())
{
int s=q.front();q.pop();rad[s]=head[s];
for(int i=head[s];i;i=e[i].next)
{
int to=e[i].to;
if(dis[to]==0&&e[i].w)
{
dis[to]=dis[s]+1;q.push(to);
}
}
}
return dis[T];
}
ll dfs(int now,ll rem)
{
if(now==T)return rem;
ll tmp=rem;
for(int i=rad[now];i;i=e[i].next)
{
int to=e[i].to;rad[now]=i;
if(dis[to]==dis[now]+1&&e[i].w)
{
ll k=min(e[i].w,tmp);
ll dlt=dfs(to,k);
e[i].w-=dlt,e[i^1].w+=dlt;
tmp-=dlt;
if(!tmp)break;
}
}
return rem-tmp;
}
int main(){
/*将图分为二分图*/
ios::sync_with_stdio(false);
ll sum=0;
cin>>m>>n;S=n*m+1;T=n*m+2;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)cin>>a[i][j],sum+=a[i][j];
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
if((i+j)%2==1)
{
add(S,(i-1)*n+j,a[i][j]);//棋盘中的为黑色的点和起点连边
if(i>1)add((i-1)*n+j,(i-2)*n+j,1e17);//将互斥的两点连边流量为inf
if(j>1)add((i-1)*n+j,(i-1)*n+j-1,1e17);
if(i<m)add((i-1)*n+j,i*n+j,1e17);
if(j<n)add((i-1)*n+j,(i-1)*n+j+1,1e17);
}
else
{
add((i-1)*n+j,T,a[i][j]);//棋盘中的为白色的点和终点连边
}
}
ll res=0;
while(bfs())res+=dfs(S,1e18);
cout<<sum-res<<endl;
return 0;
}
最大流=最小割
最小路径覆盖问题
给定一张DAG(有向无环图),n将其划分为多个集合,集合存放的是同一路径上的点,现在求集合数量最少的划分方案。
最小路径覆盖数=|G|-二分图最大匹配数(|G|是有向图中的总边数)
讲一下思路吧,套路的拆点,将每个点拆成两个,一个入点,一个出点,
如果原图中两个点之间有一条有向边,那么就将拆点后的图该点的出点连一条容量为1的边到另一点的入点,
然后建立一个超源,超汇,把超源向每个出点连边,入点向超汇连边,然后跑最大流。
每条路径的开头就是入点中没有匹配的点,跑最大流的时候记录一下每个入点对应的出点就行了。
大家都吐槽此题没写special judge,所以用vector邻接表输出方案会不对,
所以蒟蒻为自己曾是一名pas党感到庆幸,因为pascal的邻接表写法就是大家说的链式前向星,
时空常数比较小_,写习惯了,就不咋用vector了。
二分图定理之一:最小路径覆盖数=顶点数-最大匹配,这个应该都知道吧?
最小费用最大流
最小费用最大流,即求在保证最大流量下,所需花费的最小费用。对于每一条边都有一个容量和费用,可以通过费用除以流量,来获得的单位流量,单位流量可以看作距离,最小费用即为流量*最短路径。
KM算法
1.复杂度o(n4)->o(n3)
2.适用范围:带权二分图的最佳匹配。
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int MAXN = 305;
const int INF = 0x3f3f3f3f;
int love[MAXN][MAXN]; // 记录每个妹子和每个男生的好感度
int ex_girl[MAXN]; // 每个妹子的期望值
int ex_boy[MAXN]; // 每个男生的期望值
bool vis_girl[MAXN]; // 记录每一轮匹配匹配过的女生
bool vis_boy[MAXN]; // 记录每一轮匹配匹配过的男生
int match[MAXN]; // 记录每个男生匹配到的妹子 如果没有则为-1
int slack[MAXN]; // 记录每个汉子如果能被妹子倾心最少还需要多少期望值
int N;
bool dfs(int girl)
{
vis_girl[girl] = true;
for (int boy = 0; boy < N; ++boy) {
if (vis_boy[boy]) continue; // 每一轮匹配 每个男生只尝试一次
int gap = ex_girl[girl] + ex_boy[boy] - love[girl][boy];
if (gap == 0) { // 如果符合要求
vis_boy[boy] = true;
if (match[boy] == -1 || dfs( match[boy] )) { // 找到一个没有匹配的男生 或者该男生的妹子可以找到其他人
match[boy] = girl;
return true;
}
} else {
slack[boy] = min(slack[boy], gap); // slack 可以理解为该男生要得到女生的倾心 还需多少期望值 取最小值 备胎的样子
}
}
return false;
}
int KM()
{
memset(match, -1, sizeof match); // 初始每个男生都没有匹配的女生
memset(ex_boy, 0, sizeof ex_boy); // 初始每个男生的期望值为0
// 每个女生的初始期望值是与她相连的男生最大的好感度
for (int i = 0; i < N; ++i) {
ex_girl[i] = love[i][0];
for (int j = 1; j < N; ++j) {
ex_girl[i] = max(ex_girl[i], love[i][j]);
}
}
// 尝试为每一个女生解决归宿问题
for (int i = 0; i < N; ++i) {
fill(slack, slack + N, INF); // 因为要取最小值 初始化为无穷大
while (1) {
// 为每个女生解决归宿问题的方法是 :如果找不到就降低期望值,直到找到为止
// 记录每轮匹配中男生女生是否被尝试匹配过
memset(vis_girl, false, sizeof vis_girl);
memset(vis_boy, false, sizeof vis_boy);
if (dfs(i)) break; // 找到归宿 退出
// 如果不能找到 就降低期望值
// 最小可降低的期望值
int d = INF;
for (int j = 0; j < N; ++j)
if (!vis_boy[j]) d = min(d, slack[j]);
for (int j = 0; j < N; ++j) {
// 所有访问过的女生降低期望值
if (vis_girl[j]) ex_girl[j] -= d;
// 所有访问过的男生增加期望值
if (vis_boy[j]) ex_boy[j] += d;
// 没有访问过的boy 因为girl们的期望值降低,距离得到女生倾心又进了一步!
else slack[j] -= d;
}
}
}
// 匹配完成 求出所有配对的好感度的和
int res = 0;
for (int i = 0; i < N; ++i)
res += love[ match[i] ][i];
return res;
}
int main()
{
while (~scanf("%d", &N)) {
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
scanf("%d", &love[i][j]);
printf("%d\n", KM());
}
return 0;
}
数据结构
莫队算法——优雅的暴力
莫队–优雅的暴力,当遇到大量的区间询问时,假如区间的左右下标有着一定的规律,我们可以如何求解?
如:
[ 1 , 3 ] , [ 1 , 4 ] , [ 1 , 5 ] , [ 2 , 5 ] [1,3],[1,4],[1,5],[2,5] [1,3],[1,4],[1,5],[2,5]。
当然是双指针!其时间复杂度从 n 2 n^2 n2下降到 o ( n ) o(n) o(n)。
莫队就是这样一个算法,通过预处理询问顺序,来降低时间复杂度,当然,前提是能够预处理,强制在线的题目便与莫队无缘。
其预处理流程如下:
- 首先将数据分块,分块大小为size
- 将区间排序,如果区间的左端点落在同一个块中,那么我们将其按右端点大小排序。
- 如果它们的左端点不在同一块中,那么便按照左端点升序排序。
当我们处理完区间顺序之后,剩下的就是之后双指针的左右移动罢了,考虑增加和删除对与答案的影响,也就结束了。
ll sum = 0;
s[a[1]]++;
for (int i = 1; i <= m; i++)
{
while (l < q[i].l)sum += del(l++);
while (l > q[i].l)sum += add(--l);
while (r < q[i].r)sum += add(++r);
while (r > q[i].r)sum += del(r--);
ans[q[i].id] = sum;
}
那么问题来了,如何分析莫队算法的时间复杂度呢?
考虑对单一块进行询问,我们考虑最糟糕的情况,同一块中的左端点再反复横跳,先是再块的最左端,然后跑到最右端如此反复,当然,右端点是有序的,它只会后移操作。那么其实时间复杂度为 o ( s i z e ? m i + n ) o(\sqrt{size}*m_i+n) o(size??mi?+n),其中 m i m_i mi?表示再第i块中的区间数.
那么对于总体的时间复杂度为 o ( s i z e ? m + n ? ( n s i z e ) ) o(\sqrt{size}*m+n*(\frac{n}{size})) o(size??m+n?(sizen?))?。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 5e4 + 5;
struct node {
int l, r, id;
}q[maxn];
ll n, m, a[maxn], ans[maxn], l = 1, r = 1, sum, s[maxn], id[maxn], Size;
ll lef[maxn], righ[maxn];
bool cmp(struct node x, struct node y)
{
if (id[x.l] == id[y.l])
{
if(id[x.l]&1)return x.r < y.r;
return x.r>y.r;
}//排序,左端点在同一块内,按右区间升序排序 ,奇数偶数优化
return x.l < y.l;//否则,按左区间排序
}
ll add(int x)
{
ll gs = ++s[a[x]];
return s[a[x]] * (s[a[x]] - 1) / 2 - (s[a[x]] - 1)*(s[a[x]] - 2) / 2;//返回影响
}
ll del(int x)
{
ll gs = --s[a[x]];
return gs * (gs - 1) / 2 - gs * (gs + 1) / 2;//返回影响
}
ll gcd(ll a, ll b)
{
if (a == 0)return b>0?b:1;
return b == 0 ? a : gcd(b, a%b);
}
int main()
{
ios::sync_with_stdio(false);
//freopen("P1494_1.in", "r+", stdin);
cin >> n >> m;
Size = n / sqrt(m * 2 / 3);//分块大小,会影响时间复杂度。
for (int i = 1; i <= n; i++)
{
cin >> a[i];
id[i] = (i - 1) / Size + 1;
}
for (int i = 1; i <= m; i++)
{
cin >> q[i].l >> q[i].r;
q[i].id = i;
lef[i] = q[i].l;
righ[i] = q[i].r;
}
sort(q + 1, q + m + 1, cmp);
ll sum = 0;
s[a[1]]++;
for (int i = 1; i <= m; i++)
{
while (l < q[i].l)sum += del(l++);
while (l > q[i].l)sum += add(--l);
while (r < q[i].r)sum += add(++r);
while (r > q[i].r)sum += del(r--);
ans[q[i].id] = sum;
}
//cout << m << endl;
for (int i = 1; i <= m; i++)
{
ll gs = righ[i] - lef[i] + 1;
if (gs == 1) { cout << "0/1" << endl; continue; }
ll g=gcd(ans[i], gs*(gs - 1) / 2);
//cout <<i<<" "<< ans[i]<<" "<<g << endl;
cout<< ans[i] / g << '/' << gs * (gs - 1) / 2 / g << endl;
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+6;
#define ll long long
ll a[maxn],cnt=0,buc1[maxn],buc2[maxn],id[maxn],ans[maxn];
int Size;
struct mo
{
int l,r;
int pos;
bool operator <(const struct mo x)const
{
if(id[l]==id[x.l])
{
if(id[l]&1)return r<x.r;
return r>x.r;
}
return l<x.l;
}
}q[maxn];
int main()
{
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
Size=(int)sqrt(n);
for(int i=1;i<=n;i++)
{
//cin>>a[i];
scanf("%lld",&a[i]);
a[i]^=a[i-1];
id[i]=(i-1)/Size+1;
}
//for(int i=1;i<=n;i++)cout<<a[i]<<" ";cout<<endl;
for(int i=1;i<=m;i++)
{
//cin>>q[i].l>>q[i].r;
scanf("%lld%lld",&q[i].l,&q[i].r);
q[i].pos=i;
}
sort(q+1,q+m+1);
ll l=1,r=1,cnt=0;
buc1[0]=1;
buc2[a[1]]=1;
if(a[1]==k)cnt++;
for(int i=1;i<=m;i++)
{
//cout<<q[i].pos<<endl;
while(r<q[i].r)
{
buc1[a[r]]++;buc2[a[r+1]]++;
cnt+=buc1[a[r+1]^k];
// if(buc1[a[r+1]^k]>0)cout<<i<<" "<<l<<" "<<r+1<<" +"<<buc1[a[r+1]^k]<<endl;
r++;
}
while(r>q[i].r)
{
cnt-=buc1[a[r]^k];
// if(buc1[a[r]^k]>0)cout<<i<<" "<<l<<" "<<r-1<<" -"<<buc1[a[r]^k]<<endl;
buc1[a[r-1]]--;buc2[a[r]]--;
r--;
}
while(l<q[i].l)
{
cnt-=buc2[a[l-1]^k];
// if(buc2[a[l-1]^k]>0)cout<<i<<" "<<l+1<<" "<<r<<" -"<<buc2[a[l-1]^k]<<endl;
buc1[a[l-1]]--;buc2[a[l]]--;
l++;
}
while(l>q[i].l)
{
buc2[a[l-1]]++;
cnt+=buc2[a[l-2]^k];
// if(buc2[a[l-2]^k]>0)cout<<i<<" "<<l-1<<" "<<r<<" +"<<buc2[a[l-2]^k]<<endl;
l--;
buc1[a[l-1]]++;
}
ans[q[i].pos]=cnt;
}
for(int i=1;i<=m;i++)printf("%lld\n",ans[i]);
return 0;
}
2021牛客国庆
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=2e6+6;
#define scf(x) scanf("%d",&x)
int pos[maxn],a[maxn],Size,buc[maxn],cnt,ans[maxn];
struct mo
{
int l,r;
int id;
bool operator <(const struct mo y)const
{
if(pos[l]==pos[y.l])
{
if(pos[l]&1)return r<y.r;
return r>y.r;
}
return l<y.l;
}
}q[maxn];
inline void add(int x)
{
if(buc[a[x]]==0)cnt++;
buc[a[x]]++;
}
inline void del(int x)
{
if(buc[a[x]]==1&&x!=0)cnt--;
buc[a[x]]--;
}
int main()
{
int n,m;
while(~scanf("%d %d",&n,&m)){
Size=sqrt(n);
cnt=0;
for(int i=1;i<=n;i++)scf(a[i]),pos[i]=(i-1)/Size+1,buc[i]=0;
for(int i=1;i<=n;i++)
{
if(buc[a[i]]==0)cnt++;
buc[a[i]]++;
}
// cout<<cnt<<endl;
for(int i=1;i<=m;i++)scf(q[i].l),scf(q[i].r),q[i].id=i;
sort(q+1,q+m+1);
int l=0,r=0;
for(int i=1;i<=m;i++)
{
while(r<q[i].r)del(r++);
while(r>q[i].r)add(--r);
while(l<q[i].l)add(++l);
while(l>q[i].l)del(l--);
ans[q[i].id]=cnt;
}
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
}
return 0;
}
双端队列
struct Deque {
int head, rear, max_length;
int q[DEQUE_SIZE];
// 构造函数
Deque() {
head = 0;
rear = 1;
max_length = DEQUE_SIZE; //最大容量
}
// 清空
void clear() {
head = 0;
rear = 1;
}
// 判空
bool empty() {
if((head + 1) % max_length == rear) {
return true;
}
return false;
}
// 判满
bool full() {
if((rear + 1) % max_length == head) {
return true;
}
return false;
}
// 队列长度
int size() {
return (rear - head - 1 + max_length) % max_length;
}
// 返回队首元素
int front() {
if(empty()) return -1; //队列为空
return q[(head + 1) % max_length];
}
// 返回队尾元素
int back() {
if(empty()) return -1; //队列为空
return q[(rear - 1 + max_length) % max_length];
}
// 队尾插入元素
void push_back(int val) {
if(full()) return; // 队列满了
q[rear] = val;
rear = (rear + 1) % max_length;
}
// 队首插入元素
void push_front(int val) {
if(full()) return; // 队列满了
q[head] = val;
head = (head - 1 + max_length) % max_length;
}
// 队尾删除元素
void pop_back() {
if(empty()) return; //队列为空
rear = (rear - 1 + max_length) % max_length;
}
// 队首删除元素
void pop_front() {
if(empty()) return; //队列为空
head = (head + 1) % max_length;
}
};
树上dp
环基图,拆环为树
并查集
int find(int x)
{
if(a[x]==x)return x;
return a[x]=find(a[x]);
}
a[find(x)]=find(y);建立
手写堆
#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
const ll p=1e9+7;
ll heap[10000007];//模拟堆
ll a[10000007];
ll hsize=0;//堆的大小,也是堆最后一个元素的编号
inline ll read(){
ll s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline void _insert(ll node,ll num)//插入函数,思路是将元素插入到最后的叶节点,然后往上跳,直到它的父节点小于它时
{
heap[node]=num;//直接覆盖,省去了判断。若还需继续跳,再在判断中将它重新赋值
if(heap[node>>1]>num)//判断父节点是否大于它(若大于,则交换)。注意:node等于1时,它的父节点为0,值为0,必然比它小,所以不会再往上跳,所以无需加特判
{
heap[node]=heap[node>>1];
_insert(node>>1,num);//交换父子位置,继续递归
}
}
inline void _pop(ll node,ll num)//删除函数
{
heap[node]=num;//类似插入函数,直接先赋值
if((node<<1)<=hsize&&(num>heap[node<<1]||num>heap[(node<<1)|1]))//如果它有子节点,且至少有一个小于它(及可进行交换)
{
heap[node]=heap[node<<1]<heap[(node<<1)|1]?heap[node<<1]:heap[(node<<1)|1];//让更小的与它交换,保证堆的稳定性
_pop(heap[node<<1]<heap[(node<<1)|1]?node<<1:(node<<1)|1,num);//判断应走哪一个子节点
}
}
int main()
{
ll gs;
ll cz;
ll crs;
ll n;n=read();
for(int i=1;i<=n;i++)
{
ll num;
a[i]=read();
}
ll res=0;ll pop=1;
for(int i=1;i<n;i++)
{
ll r1,r2;
ll q1=1e18,q2=1e18,q3=1e18,q4=1e18;
if(pop<=n)q1=a[pop];
if(pop+1<=n)q2=a[pop+1];
if(hsize==0||q1<heap[1])
{
r1=q1,pop++;
if(hsize==0||q2<heap[1])r2=q2,pop++;
else r2=heap[1],_pop(1,heap[hsize--]);
}
else
{
r1=heap[1],_pop(1,heap[hsize--]);
if(hsize==0||q1<heap[1])r2=q1,pop++;
else r2=heap[1],_pop(1,heap[hsize--]);
}
//cout<<r1<<" "<<r2<<endl;
res=(res+r1+r2)%p;
_insert(++hsize,r1+r2);
}
cout<<res<<endl;
/*for(int zs=0;zs<gs;zs++)
{
scanf("%d",&cz);//三种操作
if(cz==1)scanf("%d",&crs),_insert(++hsize,crs);
if(cz==2)printf("%d\n",heap[1]);//堆顶即使最小值
if(cz==3)_pop(1,heap[hsize--]);//注意++、--的位置(我就在这里卡了好久/(ㄒoㄒ)/~~,30分的同学也有可能是在这里卡的)
}*/
return 0;
}
树状数组
利用lowbit构造伪树形结构,是得修改变成o(log n)
利用c[i]数组存放满足某些点的和,使其整体满足变形二叉树,当需要查询时,取处需要的c[i],这些c[i]相加的记过便是查询的前缀和。
区间查询,单点修改(类似前缀和)
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+5;
int c[maxn];//长度等于数据长度
inline int lowbit(int x){return x&(-x);}//取出x的最低位1
inline void update(int x,int y,int n){//单点更新
for(int i=x;i<=n;i+=lowbit(i))c[i]+=y;
}
inline int getsum(int x){
int ans=0;for(int i=x;i;i-=lowbit(i))ans+=c[i];
return ans;
}
int main()
{
ios::sync_with_stdio(false);
int op,n,m,x,y,num;
cin>>n>>m;
for(int i=1;i<=n;i++){cin>>num;update(i,num,n);}
for(int i=1;i<=m;i++){
cin>>op>>x>>y;
if(op==1)update(x,y,n);
else cout<<getsum(y)-getsum(x-1)<<endl;//查询类似差分,就是查询前缀和
}
return 0;
}
区间修改,单点查询
利用差分数组的思想,将数组 [ a 1 , a 2 , … … , a n ] [a_1,a_2,……,a_n] [a1?,a2?,……,an?]?转化为 [ a 1 , a 2 ? a 1 , a 3 ? a 2 , … … , a n ? a n ? 1 ] [a_1,a_2-a_1,a_3-a_2,……,a_n-a_{n-1}] [a1?,a2??a1?,a3??a2?,……,an??an?1?]
区间修改类似差分,更改l, r+1;
查修的是前缀和
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e5 + 5;
int n, m;
ll c[maxn];
int lowbit(int x) { return x & (-x); }
void add(int x,int y)
{
for (int i = x; i <= n; i += lowbit(i))c[i] += y;
}
ll getsum(int x)
{
ll ans = 0;for (int i = x; i; i -= lowbit(i))ans += c[i];return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m;
int num1,num2;
cin >> num1; add(1, num1);
for (int i = 2; i <= n; i++)cin >> num2, add(i, num2 - num1), num1 = num2;
while(m--)
{
char op;
cin >> op;
if(op=='Q')
{
int x;
cin >> x;
cout << getsum(x) << endl;
}
else
{
int l, r, x;
cin >> l >> r >> x;
add(l, x); add(r + 1, -x);
}
}
return 0;
}
线段树
1.简单的线段树
单点修改加区间查询
单点修改:先搜索,搜到待修改的点后修改,回溯过程中自下而上修改,时间复杂度logn
区间查询:返回所有被待查询区间包括的区间,时间复杂度logn
单点查询和区间修改
区间修改:在这里线段树存放的是在原基础上增加的num;
单点查询;自上而下将沿路的num都相加
2.进阶线段数
区间修改和区间查询
区间修改:当发现目前区间被待修改区间覆盖了,就将该区间加上k*长度,并且加上延迟标记;
区间查询:增加了push_down的操作,将延迟标记传递给子区间,并且增加子区间的sum;这样查询的时间与之前的时间复杂度相同
乘法线段树
其他都相同,当有乘有加时需要先乘再加;
st表
#include<iostream>
#include<stdio.h>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=2e6+6;
int f[maxn][60];//需要算好空间,不能太大
double lg2[maxn];
inline int read()
{
int x=0,fa=1;char ch=getchar();
while (!isdigit(ch)){if (ch=='-') fa=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*fa;
}
inline int search(int l,int r)
{
int s=lg2[r-l+1]/lg2[2];
return max(f[l][s],f[r-(1<<s)+1][s]);
}
int main()
{
int n,m,l,r;
n=read();m=read();
for(int i=1;i<=n;i++)cin>>f[i][0];
for(int i=1;i<=n;i++)lg2[i]=log2(i);
for(int j=1;j<=lg2[n]/lg2[2];j++)
{
for(int i=1;i<=n&&i+(1<<j)-1<=n;i++)//边界控制-1,j表示的时i之后的j位,所以要减
{
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
for(int i=1;i<=m;i++)
{
l=read();r=read();
printf("%d\n",search(l,r));
}
return 0;
}
字符串
string s1;
s1.substr(begin,end);
马拉车算法
马拉车用于解决最长回文子串问题,重点是子串,所以对于求最长回文子串的问题有一种神奇的算法——马拉车算法,神奇就神奇在时间复杂度为O(n)。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
const int maxn = 1e6 + 5;
char s[maxn * 2], str[maxn * 2];
int Len[maxn * 2], len;
void getstr() {//重定义字符串
int k = 0;
str[k++] = '@';//开头加个特殊字符防止越界
for (int i = 0; i < len; i++) {
str[k++] = '#';
str[k++] = s[i];
}
str[k++] = '#';
len = k;
str[k] = 0;//字符串尾设置为0,防止越界
}
int manacher() {
int mx = 0, id;//mx为最右边,id为中心点
int maxx = 0;
for (int i = 1; i < len; i++) {
if (mx > i) Len[i] = min(mx - i, Len[2 * id - i]);//判断当前点超没超过mx
else Len[i] = 1;//超过了就让他等于1,之后再进行查找
while (str[i + Len[i]] == str[i - Len[i]]) Len[i]++;//判断当前点是不是最长回文子串,不断的向右扩展
if (Len[i] + i > mx) {//更新mx
mx = Len[i] + i;
id = i;//更新中间点
maxx = max(maxx, Len[i]);//最长回文字串长度
}
}
return (maxx - 1);
}
int main() {
scanf("%s", s);
len = strlen(s);
getstr();
printf("%d\n",manacher());
return 0;
}
字典树(前缀树、单词查找树)
#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node
{
int cnt;
int son[26];
bool have;
node()
{
cnt=0;
memset(son,flase,sizeof(son));//太大还是别用的好
have=false;
}
}trie[800000];
int num;
void insert(string s)
{
int v,len=s.length();
int u=0;
for(int i=0;i<len;i++)
{
v=s[i]-'a';
if(trie[u].son[v]==0)trie[u].son[v]=++num,u=trie[u].son[v];
}
trie[u].have=1;
}
int find(string s)
{
int v,u=0,len=s.length();
for(int i=0;i<len;i++)
{
v=s[i]-'a';
if(trie[u].son[v]==0)return 3;+
}
if(trie[u].have==0)return 3;
if(trie[u].cnt==0)
{
trie[u].cnt++;
return 1;
}
return 2;
}
int main()
{
ios::sync_with_stdio(false);
char name[100];
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
scanf("%s",name);
insert(name);
}
scanf("%d",&m);
for(int i=1;i<=m;++i)
{
scanf("%s",name);
int p=find(name);
if(p==1)
puts("OK");
else if(p==2)
puts("REPEAT");
else if(p==3)
puts("WRONG");
}
return 0;
}
kmp模式匹配算法
时间复杂度O(n+m)
定理:假设S的长度为len,则S存在最小循环节,循环节的长度L为len-next[len],子串为S[0…len-next[len]-1]。
(1)如果len可以被len - next[len]整除,则表明字符串S可以完全由循环节循环组成,循环周期T=len/L。
(2)如果不能,说明还需要再添加几个字母才能补全。需要补的个数是循环个数L-len%L=L-(len-L)%L=L-next[len]%L,L=len-next[len]。
分为3个步骤:
1.prefix_arrary(每一位的存放的是当前字符串的最大公共前后缀;
2.move prefix_arrary(为了之后匹配服务,整体后移,首位补-1);
3.match;
#include<bits/stdc++.h>
bool SUBMIT = false;
using namespace std;
const int inf = 1000;
int nex[inf];
string s,h;
void Getnex(string m)//对kmp数组的构造
{
nex[0]=-1;
int k=-1,j=0;
while(j<m.size())
{
if(k==-1||m[k]==m[j])
{
k++;j++;
nex[j]=k;
}else
k=nex[k];
}
}
int kmp()//用kmp进行匹配
{
int k=0,j=0;
while(j<h.size())
{
if(k==-1||s[k]==h[j])
{
k++;j++;
}else{
k=nex[k];
cout<<k<<" "<<j<<endl;
}
if(k == s.size())
return j-k;
}
return -1;
}
int main()
{
string s;
cin>>s;
Getnex(s);
for(int i=0;i<=s.length();i++)cout<<nex[i]<<endl;
return 0;
}
AC自动机
ac自动机:在trie树上增加了失配指针,当匹配失败时便跳转到失配指针指向的地方。
通过该方法避免回溯产生的时间上的损失。
key1:如何构建fail指针?
1.第一层的fail指针指向的是根节点。
2.之后的fail指针指向的是父节点的fail指针指向的结点的子结点中与改结点中相同的结点。
key2:如何得到fail?
fail指针都是向上指的那么我们可以一层一层的处理结点的fail指针,那么下一层的fail指针可以直接继承父节点的fail,无需沿着fail一路向上。
那么利用bfs构建ac自动机是最好的选择。
Trie图优化
当我们沿着字典树的某一支路一直匹配下去,但我们发现匹配完了,我们会如何处理指针?
返回到根结点?那么时间复杂度会大大增加。
如何优化?我们可以将匹配结束的结点与其
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 6;
int tr[maxn][26], fail[maxn], cnt[maxn], q[maxn], id;
char s[maxn];
void build()
{
int p = 0;
for(int i=0;s[i];i++)
{
int to = s[i] - 'a';
if (tr[p][to] == 0)tr[p][to] = ++id;
p = tr[p][to];
}
cnt[p]++;
}
void get_fail()
{
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++)if (tr[0][i])q[++tt] = tr[0][i];
while(hh<=tt)
{
int ss = q[hh++];
for(int i=0;i<26;i++)
{
int to = tr[ss][i];
if (to == 0)tr[ss][i] = tr[fail[ss]][i];//如果ss不存在后继to,那么就将to向上指,指向有后继的。
else fail[to] = tr[fail[ss]][i],q[++tt]=to;//否则则将失配指针指向其父节点的下一个。
}
}
}
int main()
{
int n;
scanf("%d", &n);
for(int i=1;i<=n;i++)
{
scanf("%s", s);
build();
}
get_fail();
scanf("%s", s);
int res = 0;
for(int i=0,j=0;s[i];i++)
{
j = tr[j][s[i] - 'a'];
int p = j;
while(p&&~cnt[p])//优化,当发现cnt被搜索过就停止,类似记忆化
{
res += cnt[p];
cnt[p] = -1;
p = fail[p];
}
}
printf("%d\n", res);
}
/*
4
a
ab
ac
abc
abcd
3
*/
拓扑排序优化统计答案
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
const int L = 2e6 + 6;
int tr[maxn][26], cnt[maxn], fail[maxn], ans[maxn], du[maxn], typ[maxn], id, q[maxn], w[maxn];
char s[L], st[L];
map<int, int>m;
void build(int ty)
{
int p = 0;
for (int i = 0; s[i]; i++)
{
int to = s[i] - 'a';
if (tr[p][to] == 0)tr[p][to] = ++id;
p = tr[p][to];
}
if (typ[p] == 0)typ[p] = ty;
m[ty] = typ[p];
}
void get_fail()
{
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++)if (tr[0][i])q[++tt] = tr[0][i];
while (hh <= tt)
{
int ss = q[hh++];
for (int i = 0; i < 26; i++)
{
int to = tr[ss][i];
if (to == 0)tr[ss][i] = tr[fail[ss]][i];
else fail[to] = tr[fail[ss]][i], q[++tt] = to, du[fail[to]]++;//记录fail[to]的度数。
}
}
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%s", s);
build(i);
}
get_fail();
scanf("%s", st);
int hh = 0, tt = -1;
for (int i = 0, j = 0; st[i]; i++)
{
j = tr[j][st[i] - 'a'];
w[j] ++;//标记该点被访问了几次
}
for (int i = 1; i <= id; i++)if (du[i] == 0)q[++tt] = i;
while (hh <= tt)
{
int ss = q[hh++];
int to = fail[ss];
if (to&&to != ss) {
w[to] += w[ss];
if (du[to] == 1)q[++tt] = to;
du[to]--;
}
}
for (int i = 0; i <= id; i++)ans[typ[i]] += w[i];
for (int i = 1; i <= n; i++)printf("%d\n", ans[m[i]]);
return 0;
}
科技的力量
模拟退火
#include <bits/stdc++.h>
#define re register
using namespace std;
inline int read() { //读入优化
int X=0,w=1; char c=getchar();
while (c<'0'||c>'9') { if (c=='-') w=-1; c=getchar(); }
while (c>='0'&&c<='9') X=(X<<3)+(X<<1)+c-'0',c=getchar();
return X*w;
}
struct node { int x,y,w; };
node a[1010];
int n,sx,sy;
double ansx,ansy; //全局最优解的坐标
double ans=1e18,t; //全局最优解、温度
const double delta=0.993;//0.993; //降温系数
inline double calc_energy(double x,double y) { //计算整个系统的能量
double rt=0;
for (re int i=1;i<=n;i++) {
double deltax=x-a[i].x,deltay=y-a[i].y;
rt+=sqrt(deltax*deltax+deltay*deltay)*a[i].w;
}
return rt;
}//如何计算系统能量?
inline void simulate_anneal() { //SA主过程
double x=ansx,y=ansy;
t=2000; //初始温度
while (t>1e-14) {
double X=x+((rand()<<1)-RAND_MAX)*t;
double Y=y+((rand()<<1)-RAND_MAX)*t; //得出一个新的坐标
double now=calc_energy(X,Y);
double Delta=now-ans;
if (Delta<0) { //接受
x=X,y=Y;
ansx=x,ansy=y,ans=now;
}
else if (exp(-Delta/t)*RAND_MAX>rand()) x=X,y=Y; //以一个概率接受
t*=delta;
}
}
inline void Solve() { //多跑几遍SA,减小误差
ansx=(double)sx/n,ansy=(double)sy/n; //从平均值开始更容易接近最优解
simulate_anneal();
simulate_anneal();
simulate_anneal();
simulate_anneal();
simulate_anneal();
}
int main() {
srand(18253517); srand(rand());srand(rand()); //玄学srand
//cout << RAND_MAX;//32767
n=read();
for (re int i=1;i<=n;i++) {
a[i].x=read(),a[i].y=read(),a[i].w=read();
sx+=a[i].x,sy+=a[i].y;
}
Solve();
printf("%.3f %.3f\n",ansx,ansy);
return 0;
}
小代码,大智慧
位运算
按位构造
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
ios::sync_with_stdio(false);
ll x,s,res=1;
cin>>x>>s;
for(int i=32;i>=0;i--)
{
int xi=(x>>i)&1;
int si=(s>>i)&1;
if(xi==1)
{
if(si==1)res*=2;
if(si==0)res=0;
}
}
if((x|0)==s)res--;
cout<<res<<endl;
return 0;
}
a + b = a ∣ b + a & b a+b = a | b + a \& b a+b=a∣b+a&b