作用
对点云数据进行组织,建立树形数据结构,用于对点云进行高效的近邻搜索等(如进行K最近邻搜索、半径内邻域搜索)
概念
K维树,是在计算机科学领域用于组织在K维空间中数据点(一个点由K个变量表示)的数据结构(点云中的K维树其实就是3维树,其数据就三个维度,也就是传感器坐标系下的XYZ位置),它是一种带有额外限制的二叉搜索树。K维树在范围搜索以及近邻搜索中很有用。K维树的每一层,将会沿着某一特定维度的超平面切分所有子节点,每个父节点下的所有子节点将会被分成两部分(所以说K维树其实就是二叉搜索树)。下面将详细阐述一下K维树的切分过程,为了形象,我们点云中的3维树为例:在点云中,每个数据点有3各维度数据,故而为了对点云数据进行有效组织,我们应该建立三维树。在根节点处,我们首先可以在X维度依据一定的规则对所有子节点进行划分,然后在下一层,可以在Y维度对数据进行划分(当然也可以是在Z维度),最后在剩下的一个维度进行划分即可,在KD树的划分规则中,最有效的划分方式就是依据中值进行划分。
下图展示了一个二维KD树的例子:

代码
#include <pcl/point_cloud.h>
#include <pcl/kdtree/kdtree_flann.h>
#include <iostream>
#include <vector>
#include <ctime>
int main(int argc, char** argv)
{
srand(time(NULL)); //防止每次出现的随机数都是一样的
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>); //创建一个指向点云的指针
/**************************生成点云方法1**************************/
//初始化点云相关变量
cloud->width = 1000;
cloud->height = 1; //说明是无序点云
cloud->points.resize(cloud->width* cloud->height); //点云的点数
//生成点云
for (std::size_t t = 0; t < cloud->size(); t++)
{
cloud->points[t].x = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[t].y = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud->points[t].z = 1024.0f * rand() / (RAND_MAX + 1.0f);
}
/****************************生成点云方法2*************************/
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_1(new pcl::PointCloud<pcl::PointXYZ>);
pcl::PointXYZ point;
for (std::size_t t = 0; t < 1000; t++)
{
point.x = 1024.0f * rand() / (RAND_MAX + 1.0f);
point.y = 1024.0f * rand() / (RAND_MAX + 1.0f);
point.z = 1024.0f * rand() / (RAND_MAX + 1.0f);
cloud_1->push_back(point); //采用push_back添加点进而生成点云
}
//创建KD-Tree实例
pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
kdtree.setInputCloud(cloud);
//随机初始化一个查找点
pcl::PointXYZ searchPoint;
searchPoint.x = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.y = 1024.0f * rand() / (RAND_MAX + 1.0f);
searchPoint.z = 1024.0f * rand() / (RAND_MAX + 1.0f);
int K = 10;
std::vector<int> pointIdxNKNSearch(K); //创建一个含有K个元素的Vector变量,用于存储点的索引
std::vector<float> pointNKNSquaredDistance(K); //创建一个含有K个元素的Vector变量,用于存储到目标点的距离
std::cout << "K nearest neighbor search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with K=" << K << std::endl;
if (kdtree.nearestKSearch(searchPoint, K, pointIdxNKNSearch, pointNKNSquaredDistance) > 0) //这个函数会把索引存在pointIdxNKNSearch中
{
for (std::size_t i = 0; i < pointIdxNKNSearch.size(); ++i)
std::cout << " " << (*cloud)[pointIdxNKNSearch[i]].x
<< " " << (*cloud)[pointIdxNKNSearch[i]].y
<< " " << (*cloud)[pointIdxNKNSearch[i]].z
<< " (squared distance: " << pointNKNSquaredDistance[i] << ")" << std::endl;
}
// Neighbors within radius search
std::vector<int> pointIdxRadiusSearch;
std::vector<float> pointRadiusSquaredDistance;
float radius = 256.0f * rand() / (RAND_MAX + 1.0f);
std::cout << "Neighbors within radius search at (" << searchPoint.x
<< " " << searchPoint.y
<< " " << searchPoint.z
<< ") with radius=" << radius << std::endl;
if (kdtree.radiusSearch(searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0)
{
for (std::size_t i = 0; i < pointIdxRadiusSearch.size(); ++i)
std::cout << " " << (*cloud)[pointIdxRadiusSearch[i]].x
<< " " << (*cloud)[pointIdxRadiusSearch[i]].y
<< " " << (*cloud)[pointIdxRadiusSearch[i]].z
<< " (squared distance: " << pointRadiusSquaredDistance[i] << ")" << std::endl;
}
return 0;
}
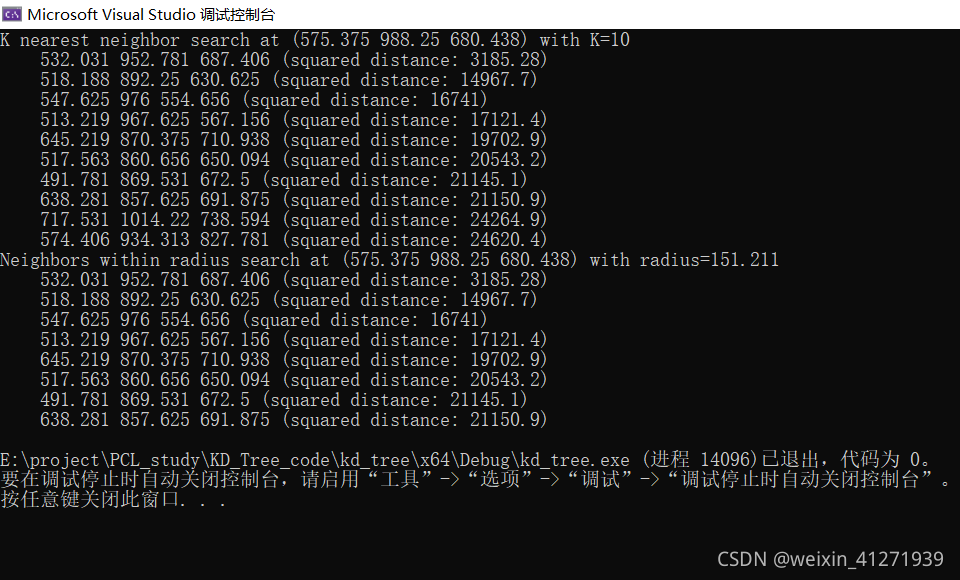
程序运行结果如下图(运行环境为visual studio2019)
参考链接
1、PCL官方教程:https://pcl.readthedocs.io/projects/tutorials/en/latest/index.html?highlight=KDtree
建议无论如何看看原滋原味的官方文档,可以先看看别人的Blog,但是最后一定看看官方文档