[C++知识库]Hands-on C++ Game Animation Programming阅读笔记（五）

Chapter 7: Exploring the glTF File Format

glTF is a standard format that can store both mesh and animation data. a file format that contains everything you need to display animated models. It’s a standard format that most three-dimensional content creation applications can export to and allows you to load any arbitrary model.

glTF: Graphics Language Transmission Format ，是一种文件格式，类似于fbx格式

本章重点：

• 了解glTF文件里存储了哪些数据
• 使用cgltf来实现glTF文件的读取
• 学会从Blender里导出glTF文件

学习之前的须知

看这张之前最好看看这个熟悉一下glTF这种文件格式：
https://www.khronos.org/files/gltf20-reference-guide.pdf.

这里会使用cgltf (https://github.com/jkuhlmann/cgltf))来parse glTF文件，有的文件可能本身是坏的，此时需要参考the glTF reference viewer at https://gltfviewer.donmccurdy.com，好像是直接把文件拖进去就能检验好坏。

glTF简介

glTF was designed and specified by the Khronos Group, for the efficient transfer of 3D content over networks.

glTF文件是一种存储3D数据的文件，在网络传输上非常高效，经常用于AR，互联网传输等领域，不过在游戏和Maya里，不如Fbx文件应用广泛。

glTF可以用一个JSON文件表示，大致分为以下内容：

• scenes和nodes： Basic structure of the scene
• cameras：View configurations for the scene
• meshes： Geometry of 3D objects
• buffers, bufferViews, accessors：Data references and data layout descriptions
• materials：Definitions of how objects should be rendered
• textures, images, samplers： Surface appearance of objects
• skins： Information for vertex skinning
• animations：Changes of properties over time

各个部分之间的关系如下图所示：

glTF索引的文件路径
glTF文件并不会包含里面所有的资源，可以用存uri的方式来代表路径，如下所示：

// 注意: json文件里并不支持注释...
"buffers": [
 {
 "uri": "buffer01.bin"	// 指的是bin文件里的数据, 可能是animation数据、几何数据等
 "byteLength": 102040,
 }
],
"images": [
 {
 "uri": "image01.png"
 }
],

还可以用include path的方式来写JSON文件，base64代表这个data是一个base64 encoded string(The data URI defines the MIME type, and contains the data as a base64 encoded string)：

// Buffer data:
"data:application/gltf-buffer;base64,AAABAAIAAgA..."
//Image data (PNG):
"data:image/png;base64,iVBORw0K..."

buffers, bufferViews, accessors

• buffers: contain the data that is used for the geometry of 3D models, animations, and skinning.
• bufferViews: describes what is in a buffer. 相当于buffer的附加信息，比如要取buffer的哪部分内容，并且它可以告诉我Buffer是vertex buffer还是index buffer
• accessors: define the exact type and layout of the data. buffer具体怎么变为数据的

This accessor references a buffer view and the buffer view references a buffer.
The buffer view describes what is in a buffer. If a buffer contains the information for glBufferData, then a buffer view contains some of the parameters to call glVertexAttribPointer
An accessor stores higher-level information, it describes the type of data you are dealing with

在OpenGL里，需要使用glBufferData和glVertexAttribPointer两个函数来描述Buffer，这里的Buffer相当于glBufferData里的内容，而bufferView和accessors一起组成了glVertexAttribPointer里的内容（或者是index buffer里的内容）

比如：

// Each of the buffers refers to a binary data file, using a URI. 
"buffers": [
 {
 "byteLength": 35,
 "uri": "buffer01.bin"
 }
],

// bufferView与Buffer一一对应, 有点像是vbo的vao, 应用定义buffer的一部分数据
"bufferViews": [
 {
 "buffer": 0,
 "byteOffset": 4,
 "byteLength": 28,
 "byteStride": 12,
 "target": 34963
 }
],

// The accessors define how the data of a bufferView is interpreted.
"accessors": [
 {
 "bufferView": 0,
 "byteOffset": 4,
 "type": "VEC2",
 "componentType": 5126,// 代表GL_FLOAT
 "count": 2, // 两个float
 // The range of all values is stored in the min and max property.
 "min" : [0.1, 0.2]
 "max" : [0.9, 0.8]
 }
]

Exploring how glTF files are stored

glTF文件一般用JOSN文件或者二进制文件来表示，JOSN文件一般用.gltf后缀表示，二进制文件一般用.glb后缀表示

glTF文件可以用三种方式来存储，如下图所示，是Blender里导出glTF文件时可以设置的选项，可以看到，glTF文件里可以包含多个文件，内部会分为多个chunk，导出的时候可以选择要不要一起放到一个glTF文件里(感觉跟fbx文件有点像)

本书里提供的glTF文件都是图中的第二种文件(glTF embedded format)，就是JOSN的文本文件，不过后面还会支持其他两种格式的glTF文件。

glTF files store a scene, not a model

这个跟fbx也是一样的，除了模型，glTF文件还可以存储Cameras和PBR材质等，这里列举出glTF文件里包含的用于动画的内容——不同类型的mesh数据：

• static mesh
• morph targets
• skinned mesh(就是static mesh with weights of joints)

Exploring the glTF format

The root of a glTF file is the scene. A glTF file can contain one or more scenes. A scene contains one or more nodes. A node
can have a skin, a mesh, an animation, a camera, a light, or blend weights attached to it. Meshes, skins, and animations each store large chunks of information in buffers. To access a buffer, they contain an accessor that contains a buffer view, which in turn contains the buffer

glTF文件的root就是scene，一个glTF文件可以有一个或者多个scene，每个scene包含至少一个node，一个node上面可以存mesh、camera、light、skin等数据的引用，这些数据都存在buffers里，它们都有一个accessor，这个accessor包含了一个buffer view，这个buffer view又包含了对应的buffer(?)

可以看看下面这个图帮助理解：

The parts you need for animation

下图是一个简单版的glTF里动画相关的部分的关系图：

To implement skinned animations, you won’t need lights, cameras, materials, textures, images, and samplers.

读取数据

读取Mesh、skin和animation对象都需要一个glTF accessor，This accessor references a buffer view and the buffer view references a buffer，如下所示是它们的关系：

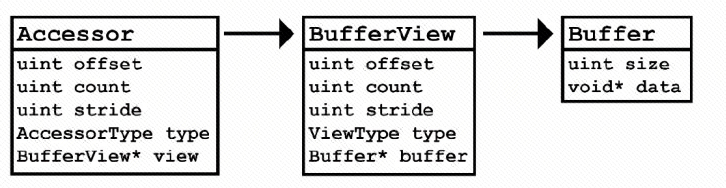
示例代码如下：

// 把accessor里的Buffer数据里转为float数组
vector<float> GetPositions(const GLTFAccessor& accessor) 
{
	// 有一种特殊的accessor, 是用来分隔buffer的, 这种应该不可以提取数据
	assert(!accessor.isSparse);
	
	// 获取bufferView和buffer的引用
	const GLTFBufferView& bufferView = accessor.bufferView;
	const GLTFBuffer& buffer = bufferView.buffer;
	
	// GetNumComponents Would return 3 for a vec3, etc., 应该是返回基本数据类型的个数
	uint numComponents = GetNumComponents(accessor);
	
	vector<float> result;
	// accessor.count代表element的个数, numComponents代表每个element里的C++的primitive type对象的个数
	result.resize(accessor.count * numComponents);
	
	// Find where in the buffer the data actually starts
	uint offset = accessor.offset + bufferView.offset;
	
	// 逐一挖取buffer里的数据
	for (uint i = 0; i < accessor.count; ++i)
	{
		// 获取指向当前元素地址的指针
		uint8* data = buffer.data + offset + accessor.stride * i;
		// Loop trough every component of current element
		float* target = result[i] * componentCount;// 代码写错了吧?
		for (uint j = 0; j < numComponents; ++j) 
		{
			// Omitting normalization
			// Omitting different storage types
			target[j] = data + componentCount * j;
		}
	}
	
	return result;
}

加入cgltf库

如果从头读取glTF文件，那么要从JSON parser写起，这里没必要写这么底层的，所以把cgltf集成进来了，这里的库都实现在头文件里了，所以只从github.com/jkuhlmann/cgltf/blob/master/cgltf.h下载头文件，加到项目中就行了。

然后再添加一个cgltf.c文件，保证该头文件得到了编译，内容如下：

#pragma warning(disable : 26451)
#define _CRT_SECURE_NO_WARNINGS
#define CGLTF_IMPLEMENTATION
#include "cgltf.h"

创建glTF Loader

创建负责读取的Loader函数，这里创建了俩全局函数，没有创建类，头文件如下：

// 简单的两个接口, 一个负责读取, 一个负责销毁读取的缓存
#ifndef _H_GLTFLOADER_
#define _H_GLTFLOADER_

#include "cgltf.h"

// 返回一个cgltf_data对象, 这个对象包含了所有的glTf里的内容
cgltf_data* LoadGLTFFile(const char* path);
void FreeGLTFFile(cgltf_data* handle);

#endif

再创建对应cpp文件：

#include "GLTFLoader.h"
#include <iostream>

cgltf_data* LoadGLTFFile(const char* path)
{
	// 加载之前, 要创建一个cgltf_options类的对象
	cgltf_options options;
	memset(&options, 0, sizeof(cgltf_options));
	// 使用库文件, 把data和options都读取出来
	cgltf_data* data = NULL;
	// cgltf_result是个枚举
	cgltf_result result = cgltf_parse_file(&options, path, &data);

	// check
	if (result != cgltf_result_success)
	{
		std::cout << "Could not load input file: " << path << "\n";
		return 0;
	}

	// 根据options和path, 把数据读到data里, 这里的options和path传入的都是const 
	result = cgltf_load_buffers(&options, data, path);
	if (result != cgltf_result_success)
	{
		cgltf_free(data);
		std::cout << "Could not load buffers for: " << path << "\n";
		return 0;
	}

	// 再次check
	result = cgltf_validate(data);
	if (result != cgltf_result::cgltf_result_success)
	{
		cgltf_free(data);
		std::cout << "Invalid gltf file: " << path << "\n";
		return 0;
	}
	return data;
}

void FreeGLTFFile(cgltf_data* data)
{
	if (data == 0)
		std::cout << "WARNING: Can't free null data\n";
	else
		cgltf_free(data);
}

.fbx、.blend文件转换为.glTF文件

由于这里只能读取glTF文件，所有这里介绍一种方法，利用Blender，把.fbx和.blend文件转换为glTF文件

打开Blender，如果该文件是.blend文件，则直接打开即可，如果是.DAE或者.FBX文件，则需要把它重新导入Blender。打开Blender，删除Blender里的默认Cube，选择File->Import，打开文件后，选择File->Export，导出glTF2.0文件即可，可选择多种格式，如下图所示：

Chapter 8: Creating Curves, Frames, and Tracks

老版的动画是把关键帧处的所有人物的joints的数据都存储进来，但是这样很浪费内存。现阶段的动画就科学多了，它是用Curve来保存动画数据的，如下图所示：

本章重点：

• 理解cubic Bézier splines和对它们取值的方式
• 理解cubic Hermite splines和对它们取值的方式
• 了解常用插值方法

Understanding cubic Bézier splines

一个Bézier spline有四个点，两个点用于插值，两个点是control points，用于帮助生成曲线，如下图所示是 一个cubic Bezier spline：

可以研究一下这个曲线是怎么生成的，要从P1插值得到P2，根据C1、C2两个控制点，可以连接得到：

其中，A、B、C都是三个线段的中点。可以按照同样的方式继续取中点，得到：

再做一次相同的做法，还是取0.5部分的中点，如下图所示，得到最后的R点就是Bezier spline上的一个点：

注意，这只是插值的一个0.5部分处的点而已，各个部分的点都经过这么处理，才能得到最终的Bezier spline，在这个过程中，四个点插值一次，变成了三个点，三个点再插值一次，得到两个点，。

相关代码如下：

// Bezier曲线本质上只有四个点
template<typename T>
class Bezier 
{
public:
	T P1; // Point 1
	T C1; // Control 1
	T P2; // Point 2
	T C2; // Control 2
};


// 相当于取到贝塞尔Spline的t部分上的点, t在[0, 1]里
template<typename T>
inline T Interpolate(Bezier<T>&curve, float t) 
{
	// lerp第一次, 四个点得到ABC
	T A = lerp(curve.P1, curve.C1, t);
	T B = lerp(curve.C2, curve.P2, t);
	T C = lerp(curve.C1, curve.C2, t);
	// lerp第二次, 三个点得到ED
	T D = lerp(A, C, t);
	T E = lerp(C, B, t);
	// lerp第三次, 两个点得到最后的R
	T R = lerp(D, E, t);
	return R;
}

下面介绍绘制贝塞尔曲线的方法，其实就是把上面这个函数按照不同的比例t，得到很多个点，然后把这些点连接起来，近似表示贝塞尔曲线即可，代码如下：

// 基于四个点, 创建一条贝塞尔曲线
Bezier<vec3> curve;
curve.P1 = vec3(-5, 0, 0);
curve.P2 = vec3(5, 0, 0);
curve.C1 = vec3(-2, 1, 0);
curve.C2 = vec3(2, 1, 0);

// 这是四个颜色
vec3 red = vec3(1, 0, 0);
vec3 green = vec3(0, 1, 0);
vec3 blue = vec3(0, 0, 1);
vec3 magenta = vec3(1, 0, 1);

// 用四种不同颜色绘制代表贝塞尔曲线的四个点
DrawPoint(curve.P1, red);
DrawPoint(curve.C1, green);
DrawPoint(curve.P2, red);
DrawPoint(curve.C2, green);

// Draw handles
DrawLine(curve.P1, curve.C1, blue);
DrawLine(curve.P2, curve.C2, blue);

// Draw the actual curve
// Resolution is 200 steps since last point is i + 1
for (int i = 0; i < 199; ++i) 
{
	float t0 = (float)i / 199.0f;
	float t1 = (float)(i + 1) / 199.0f;
	vec3 thisPoint = Interpolate(curve, t0);
	vec3 nextPoint = Interpolate(curve, t1);
	DrawLine(thisPoint, nextPoint, magenta);
}

从上面的例子可以看出，可以通过六次线性插值完成最终的Bezier插值函数，不过上面的函数还要调用Lerp函数，并不是最优化的代码写法，这里作者对其进行数学的优化，得到的新的函数如下：

template<typename T>
inline T Interpolate(const Bezier<T>& curve, float t) 
{
	return curve.P1 * ((1 - t) * (1 - t) * (1 - t)) +
		curve.C1 * (3.0f * ((1 - t) * (1 - t)) * t) +
		curve.C2 * (3.0f * (1 - t) * (t * t)) +
		curve.P2 *(t * t * t);
}

这其实就是贝塞尔插值的分解形式，把它变成了四个t的三次函数的和，如下图所示：

由于这里的t是三次函数，所以这里的贝塞尔spline属于cubic spline

Understanding cubic Hermite splines

The most common spline type used in animation for games is a cubic Hermite spline.

Unlike Bézier, a Hermite spline doesn’t use points in space for its control; rather, it uses the
tangents of points along the spline. You still have four values, as with a Bézier spline, but they are interpreted differently. With the Hermite spline, you don’t have two points and two control points; instead, you have two points and two slopes. The slopes are also referred to as tangents—throughout the rest of this chapter, the slope and tangent terms will be used interchangeably

游戏的动画行业用到最常用的spline类型就是cubic Hermite spline，Bezier Spline可以用四个点来表示，两个points和两个control points，而Hermite spline也可以用四个点来表示，两个points和两个slopes，这里的slopes跟tangents(切线)的概念是一样的，具体的Curve长这样，可以看到是两个点，加两个切线的表达方式：

其函数表达如下：

对应的代码为：

template<typename T>
T Hermite(float t, T& p1, T& s1, T& p2, T& s2) 
{
	return p1 * ((1.0f + 2.0f * t) * ((1.0f - t) * (1.0f - t))) 
		+ s1 * (t * ((1.0f - t) * (1.0f - t)))
		+ p2 * ((t * t) * (3.0f - 2.0f * t))
		+ s2 * ((t * t) * (t - 1.0f));
}

The glTF file format supports the constant, linear, and cubic interpolation types. You just learned how to do cubic interpolation, but you still need to implement both constant and linear interpolation.

Hermite Spline与Bezier Spline

有二者互相转化的方法，但相关内容不在本书涵盖内容里。一些3D建模软件，比如Maya，可以让动画师使用Hermite Splines来创建动画，但是也有别的3D建模软件，比如Blender 3D，使用的是Bezier Curves.

动画本质就是一堆Property随时间的Curve，这里提到的hermite Soline和Bezier Spline是最常见的两种Curve

Interpolation types

也就是三种：

• Constant
• Linear
• Cubic: 这本书里用到的Cubic Curve是Hermite Spline，前面只是介绍了Bezier Spline，但后面不会使用到它。

三种类型依次如下图所示，注意这里的Constant Curve并不是一直是不变常量的Curve，从左到右感觉越来越高级了：

Creating the Frame struct

这里要考虑，一个动画，每帧的具体数据是什么，假设这个动画，只是一个Property的Curve的应用，那么对于Linear和Constant类型的Curve来说，它每帧的数据，其实就是一个value，和对应的time。

对于Cubic类型的Curve，它的帧数据要复杂一些，除了本身的value和对应的time，还需要存储该处的tangent，这里的切线有两个，一个是incoming切线，一个是outgoing切线，前者用于对在control point的前面的时间点的evaluation，后者是则是对control point的后面时间点的evaluation。

A Hermite curve is made by connecting Hermite splines. (Curve和splines的区别?) Each control point consists of a time, a value, an incoming tangent, and an outgoing tangent. The incoming tangent is used if the control point is evaluated with the point that comes before it. The outgoing tangent is used if the control point is evaluated with the point that comes after it.

一个Property的Curve数据，是多个关键帧数据的集合，每个关键帧的数据包含time、出入的tangent和对应的Property的值，具体的可以有两个表示方法：

• 第一种方法，类似于Unity的动画处理方法，就是把所有的Property都细分为每个标量对应的Curve，比如Position可以分解为x、y、z三个变量的Curve
• 第二种方法是设计specialized的frame和curve类型，比如设计scalar frame、vector frame和quaternion frame三种specialized frame类型

第二种方法会比第一种方法更好写代码，但是第一种方法更省内存，因为他每个property都可以化解为一个个scalar的curve(比如float的curve)，.glTF文件里就是按照这种方式存储Animation Tracks的，而第二种，比如一个Vector3，它在动画里可能只有x和y变了，但是第二种是把它当整体存储的，所以curve也会带有z的数据，这就会消耗多的内存。

接下来就可以实现Frame类了，这是一个模板类，代码如下：

#ifndef _H_FRAME_
#define _H_FRAME_

// 这种模板的写法之前看的不多, 之前模板的<>里必须填类型
// 而这种写法把T类型specialized为unsigned int, 而且这里还加了具体类型的变量N
// 此时的<>里必须填unsigned int类型的值
template<unsigned int N>
class Frame
{
public:
	float mValue[N];// 这个Property由几个float组成
	float mIn[N];
	float mOut[N];
	float mTime;
};

// 三种specialized Frame
typedef Frame<1> ScalarFrame;
typedef Frame<3> VectorFrame;
typedef Frame<4> QuaternionFrame;

#endif

创建Track类

A Track class is a collection of frames. Interpolating a track returns the data type of the track;

Track 本质上就是frames的集合，也就是一组帧数据，一个Track最少要有两个frame对象。既然Track是frames的集合，这里定义了三种特化的frame，自然也需要把Track定义为模板类，并且实现三个特化版本，头文件代码如下：

#ifndef _H_TRACK_
#define _H_TRACK_

#include <vector>
#include "Frame.h"
#include "vec3.h"
#include "quat.h"
#include "Interpolation.h"

// 这里认为所有的T类型都是由float组成的, N是float的个数
// 比如Track<vec3, 3>
template<typename T, int N>
class Track 
{
protected:
	// 一个Track本质上只有这两样东西: frames的集合和插值类型
	std::vector<Frame<N>> mFrames;
	Interpolation mInterpolation;
protected:
	// protected下面提供的是一些helper函数
	T SampleConstant(float time, bool looping);
	T SampleLinear(float time, bool looping);
	T SampleCubic(float time, bool looping);
	T Hermite(float time, const T& point1, const T& slope1,	const T& point2, const T& slope2);
	int FrameIndex(float time, bool looping);
	float AdjustTimeToFitTrack(float time, bool looping);
	T Cast(float* value);
public:
	Track();
	void Resize(unsigned int size);
	unsigned int Size();
	Interpolation GetInterpolation();
	void SetInterpolation(Interpolation interpolation);
	// 获取第一帧的时间
	float GetStartTime();
	// 获取最后一帧的时间
	float GetEndTime();
	// 对Curve进行采样
	T Sample(float time, bool looping);
	// 重载[], 方便返回第i帧的Frame数据
	Frame<N>& operator[](unsigned int index);
};

typedef Track<float, 1> ScalarTrack;
typedef Track<vec3, 3> VectorTrack;
typedef Track<quat, 4> QuaternionTrack;

#endif 

具体的cpp代码如下：

#include "Track.h"

template Track<float, 1>;
template Track<vec3, 3>;
template Track<quat, 4>;

// namespace下定义一些helper的全局内联函数, 这些代码其实可以放到单独的header里
namespace TrackHelpers 
{
	// float的线性插值
	inline float Interpolate(float a, float b, float t) 
	{
		return a + (b - a) * t;
	}
	
	// vec3的线性插值
	inline vec3 Interpolate(const vec3& a, const vec3& b, float t) 
	{
		return lerp(a, b, t);
	}

	// 四元数的线性插值
	inline quat Interpolate(const quat& a, const quat& b, float t) 
	{
		// 虽然这里叫mix函数, 但是本质还是俩vec4的线性插值操作
		quat result = mix(a, b, t);
		if (dot(a, b) < 0) // Neighborhood
			result = mix(a, -b, t);
		
		return normalized(result); //NLerp, not slerp
	}
	
	// 对于vec3,float和quaternion, 只有quaternion需要矫正为单元四元数
	// 这里为了通用接口, 所有的Properry类型都要实现这个AdjustHermiteResult函数
	inline float AdjustHermiteResult(float f) 
	{
		return f;
	}

	inline vec3 AdjustHermiteResult(const vec3& v) 
	{
		return v;
	}

	// 归一化
	inline quat AdjustHermiteResult(const quat& q) 
	{
		return normalized(q);
	}

	// 只有quaternion的插值有neighborhood问题
	inline void Neighborhood(const float& a, float& b) { }
	inline void Neighborhood(const vec3& a, vec3& b) { }
	inline void Neighborhood(const quat& a, quat& b) 
	{
		if (dot(a, b) < 0)
			b = -b;
	}
}; // End Track Helpers namespace

// 默认ctor, 默认插值类型为线性插值
template<typename T, int N>
Track<T, N>::Track() 
{
	mInterpolation = Interpolation::Linear;
}


template<typename T, int N>
float Track<T, N>::GetStartTime() 
{
	return mFrames[0].mTime;
}

template<typename T, int N>
float Track<T, N>::GetEndTime() 
{
	return mFrames[mFrames.size() - 1].mTime;
}

// Sample的时候根据插值类型来
template<typename T, int N>
T Track<T, N>::Sample(float time, bool looping) 
{
	if (mInterpolation == Interpolation::Constant)
		return SampleConstant(time, looping);
	else if (mInterpolation == Interpolation::Linear)
		return SampleLinear(time, looping);
	
	return SampleCubic(time, looping);
}

// 返回第i帧的Frame对象
template<typename T, int N>
Frame<N>& Track<T, N>::operator[](unsigned int index) 
{
	return mFrames[index];
}

// vector的resize
template<typename T, int N>
void Track<T, N>::Resize(unsigned int size) 
{
	mFrames.resize(size);
}

template<typename T, int N>
unsigned int Track<T, N>::Size() 
{
	return mFrames.size();
}

template<typename T, int N>
Interpolation Track<T, N>::GetInterpolation() 
{
	return mInterpolation;
}

template<typename T, int N>
void Track<T, N>::SetInterpolation(Interpolation interpolation) 
{
	mInterpolation = interpolation;
}

// 这个函数会被SampleCubic函数调用
// 具体的是采样一个Hermite Curve, 返回t比例处的property
template<typename T, int N>
T Track<T, N>::Hermite(float t, const T& p1, const T& s1, const T& _p2, const T& s2) 
{
	float tt = t * t;
	float ttt = tt * t;

	// 其实只有T为quaternion时, 才需要对p2进行neighborhood处理
	T p2 = _p2;
	TrackHelpers::Neighborhood(p1, p2);

	// 各个系数是基于t的三次方函数
	float h1 = 2.0f * ttt - 3.0f * tt + 1.0f;
	float h2 = -2.0f * ttt + 3.0f * tt;
	float h3 = ttt - 2.0f * tt + t;
	float h4 = ttt - tt;

	// 其实只有T为quaternion时, 才需要对结果进行归一化处理
	T result = p1 * h1 + p2 * h2 + s1 * h3 + s2 * h4;
	return TrackHelpers::AdjustHermiteResult(result);
}

// 根据时间获取对应的帧数, 其实是返回其左边的关键帧
// 注意这里的frames应该是按照关键帧来存的, 比如有frames里有三个元素, 可能分别对应的时间为
// 0, 4, 10, 那么我input time为5时, 返回的index为1, 代表从第二帧开始
// 这个函数返回值保证会在[0, size - 2]区间内
template<typename T, int N>
int Track<T, N>::FrameIndex(float time, bool looping) 
{
	unsigned int size = (unsigned int)mFrames.size();
	if (size <= 1)
		return -1;
	
	if (looping) 
	{
		float startTime = mFrames[0].mTime;
		float endTime = mFrames[size - 1].mTime;
		float duration = endTime - startTime;

		time = fmodf(time - startTime, endTime - startTime);
		if (time < 0.0f) 
			time += endTime - startTime;
		
		time = time + startTime;
	}
	else 
	{
		if (time <= mFrames[0].mTime)
			return 0;
		// 注意, 只要大于倒数第二帧的时间, 就返回其帧数
		// 也就是说, 这个函数返回值在[0, size - 2]区间内
		if (time >= mFrames[size - 2].mTime)
			return (int)size - 2;
	}
	
	// time的下边界确定以后
	// 从后往前遍历所有的帧对应的时间, 找到time的上边界
	for (int i = (int)size - 1; i >= 0; --i) 
	{
		if (time >= mFrames[i].mTime)
			return i;
	}
	
	// Invalid code, we should not reach here!
	return -1;
} // End of FrameIndex

// 其实就是保证time在动画对应的播放时间区间内, loop为false就是Clamp到此区间
// 只是为了方便播放的计算时间的API
// loop为true就是对区间取模
template<typename T, int N>
float Track<T, N>::AdjustTimeToFitTrack(float time, bool looping) 
{
	unsigned int size = (unsigned int)mFrames.size();
	if (size <= 1)
		return 0.0f;

	float startTime = mFrames[0].mTime;
	float endTime = mFrames[size - 1].mTime;
	float duration = endTime - startTime;
	if (duration <= 0.0f)
		return 0.0f;
	if (looping) 
	{
		time = fmodf(time - startTime, endTime - startTime);
		if (time < 0.0f)
			time += endTime - startTime;
		
		time = time + startTime;
	}
	else 
	{
		if (time <= mFrames[0].mTime) 
			time = startTime;
		if (time >= mFrames[size - 1].mTime)
			time = endTime;
	}

	return time;
}

// 举个AdjustTimeToFitTrack的例子:
//Track<float, 1> t;// t是代表时间的Track
//float mAnimTime = 0.0f;
//void Update(float dt)
//{
// 	// dt: delta time of frame
//	mAnimTime = t.AdjustTimeToFitTrack(mAnimTime + dt);
//}


// 三个Cast函数, 用于把数组转型为T实际对应的类型
// 这里认为所有的数据本质上都是float*
// 然后写模板特化, 把float*解析为不同的类型的数据
template<> float Track<float, 1>::Cast(float* value) 
{
	return value[0];
}

template<> vec3 Track<vec3, 3>::Cast(float* value) 
{
	return vec3(value[0], value[1], value[2]);
}

template<> quat Track<quat, 4>::Cast(float* value) 
{
	quat r = quat(value[0], value[1], value[2], value[3]);
	return normalized(r);
}


template<typename T, int N>
T Track<T, N>::SampleConstant(float time, bool looping) 
{
	// 获取时间对应的帧数, 取整
	int frame = FrameIndex(time, looping);
	if (frame < 0 || frame >= (int)mFrames.size())
		return T();

	// Constant曲线不需要插值, mFrames里应该只有关键帧的frame数据
	return Cast(&mFrames[frame].mValue[0]);
	// 为啥要转型? 因为mValue是float*类型的数组, 这里的操作是取从数组地址开始, Cast为T类型 
}

template<typename T, int N>
T Track<T, N>::SampleLinear(float time, bool looping) 
{
	// 找到左边的关键帧对应的id
	int thisFrame = FrameIndex(time, looping);
	if (thisFrame < 0 || thisFrame >= (int)(mFrames.size() - 1))
		return T();
		
	// 右边的关键帧对应的id	
	int nextFrame = thisFrame + 1;

	// 其实这段代码应该只有looping为true的时候会起作用
	float trackTime = AdjustTimeToFitTrack(time, looping);

	// 后面就是线性插值了
	float frameDelta = mFrames[nextFrame].mTime - mFrames[thisFrame].mTime;
	if (frameDelta <= 0.0f)
		return T();
	
	float t = (trackTime - mFrames[thisFrame].mTime) / frameDelta;

	// mValue是mFrames里代表关键帧数据的数组, 比如T为vec3时, mValue就是
	// 一个float[3]的数组
	T start = Cast(&mFrames[thisFrame].mValue[0]);
	T end = Cast(&mFrames[nextFrame].mValue[0]);

	return TrackHelpers::Interpolate(start, end, t);
}

// 重点函数
template<typename T, int N>
T Track<T, N>::SampleCubic(float time, bool looping) 
{
	// 前面的步骤跟上面的差不多
	// 获取左右关键帧的id
	int thisFrame = FrameIndex(time, looping);
	if (thisFrame < 0 || thisFrame >= (int)(mFrames.size() - 1))
		return T();
	
	int nextFrame = thisFrame + 1;

	float trackTime = AdjustTimeToFitTrack(time, looping);
	float frameDelta = mFrames[nextFrame].mTime - mFrames[thisFrame].mTime;
	if (frameDelta <= 0.0f)
		return T();
	
	// t的算法也一样, t代表两帧之间的比例
	float t = (trackTime - mFrames[thisFrame].mTime) / frameDelta;

	// 获取左边关键帧的point和slope, 如果point是vec2, 那么slope也是vec2, 所以类型都是T
	T point1 = Cast(&mFrames[thisFrame].mValue[0]);
	T slope1;// = mFrames[thisFrame].mOut * frameDelta;
	// 注意：这里取的是左边关键帧的Out切线, In切线没有用到, 这里的Out和In
	// 由于是Delta T的切线, 所以跟T类型是一模一样的
	// 而且这里用到的是memcpy函数, 不是Cast函数, 因为对于quaternnion这种类型的T
	// Cast函数会做归一化处理, 而这里是算切线, 不需要归一化
	memcpy(&slope1, mFrames[thisFrame].mOut, N * sizeof(float));
	slope1 = slope1 * frameDelta;

	T point2 = Cast(&mFrames[nextFrame].mValue[0]);
	T slope2;// = mFrames[nextFrame].mIn[0] * frameDelta;
	// 注意：这里取的是右边关键帧的In切线, Out切线没有用到
	memcpy(&slope2, mFrames[nextFrame].mIn, N * sizeof(float));
	slope2 = slope2 * frameDelta;

	// 根据这四个值组成的Curve, 然后输入t部分返回的Property的T的值
	return Hermite(t, point1, slope1, point2, slope2);
}

关于Track类的思考

Track类到底是个啥，Property对应的Curve的数据吗，好像不是，因为它好像可以用于时间，比如这段代码：

// 举个AdjustTimeToFitTrack的例子:
Track<float, 1> t;// t是代表时间的Track
float mAnimTime = 0.0f;
void Update(float dt)
{
 	// dt: delta time of frame
	mAnimTime = t.AdjustTimeToFitTrack(mAnimTime + dt);
}

Track的本质代码：

// 类型T的对象用N个float组成的数组表示
template<typename T, int N>
class Track 
{
protected:
	// 一个Track本质上只有这两样东西: frames的集合和插值类型
	std::vector<Frame<N>> mFrames;
	Interpolation mInterpolation;
	...
}

template<unsigned int N>
class Frame
{
public:
	float mValue[N];// 这个Property由几个float组成
	float mIn[N];
	float mOut[N];
	float mTime;
};

分析一下Track的特点：

• Track本质的数据就是一个数组，类似C++ STL的泛型vector，虽然都是泛型，但是STL的vector里存的是T的对象，但是Track的数组vector里存的是Frame的对象，这里的Frame就是个简单的Class，代表关键帧数据，里面除了时间是一个float变量，其他的都用float*表示，而这里的T，代表了Frame结构体里的mValue本身是一个什么类型的变量（为什么这里的Frame不是一个模板，T与Frame完全没有关系呢，而是把T的定义放到了Track里，也就是说，单独一个Frame对象，不结合Track，是无法起作用的）
• Cast函数，用于把float数组转型为T对象，这里的float数组，其实是个很小的数组，它只可能对应一个T对象，比如T为vec3时，float*的size为3

所以说，我理解的Track，非常类似于Unity里的Curve数据，它本质上就是一个Property随时间变化的Curve。

可以再来看看之前的代码：

// 这个Track的本身就是时间的Curve
Track<float, 1> t;
float mAnimTime = 0.0f;
void Update(float dt)
{
 	// dt: delta time of frame
	mAnimTime = t.AdjustTimeToFitTrack(mAnimTime + dt);
}

其实这个Track，也是一种Curve，它的变量是time，得到的结果与time和动画本身的周期有关，其曲线如下图所示：

把position track、quaternion track和scale track组合成transform track

其实跟Unity里的Animation里的数据差不多，里面也是LocalPosition、LocalRotation和LocalScale的Curve，但是这书里的动画好像没有Scale的动画数据，所以就只组合了前俩。

这里有两种做法：

1. 为每个Model上的Bone都创建Transform Track，优点是查询方便，缺点是消耗内存大，即使没有动画的Bone也会有对应的Track
2. 只为Model上存在动画的Bone创建Transform Track，然后记录每个Track对应的Bone ID，实际用的时候，会遍历每个Track，根据其ID找到对应的Bone

显然方法二更好，这里选择方法二，先创建TransformTrack的头文件：

#ifndef _H_TRANSFORMTRACK_
#define _H_TRANSFORMTRACK_

#include "Track.h"
#include "Transform.h"

class TransformTrack 
{
protected:
	unsigned int mId;// 对应Bone的Id
	// 居然不是写的Track<vec3, float>, 而是又自己定义了VectorTrack类和QuaternionTrack类
	VectorTrack mPosition;
	QuaternionTrack mRotation;
	VectorTrack mScale;
public:
	TransformTrack();
	unsigned int GetId();
	void SetId(unsigned int id);
	VectorTrack& GetPositionTrack();
	QuaternionTrack& GetRotationTrack();
	VectorTrack& GetScaleTrack();
	float GetStartTime();
	float GetEndTime();
	bool IsValid();
	Transform Sample(const Transform& ref, float time, bool looping);
};

#endif

下面是这些函数的实现，基本就是三个Track的缝合怪，没啥新东西：

#include "TransformTrack.h"

TransformTrack::TransformTrack() 
{
	mId = 0;
}

unsigned int TransformTrack::GetId() 
{
	return mId;
}

void TransformTrack::SetId(unsigned int id) 
{
	mId = id;
}

VectorTrack& TransformTrack::GetPositionTrack() 
{
	return mPosition;
}

QuaternionTrack& TransformTrack::GetRotationTrack() 
{
	return mRotation;
}

VectorTrack& TransformTrack::GetScaleTrack() 
{
	return mScale;
}

// 只要三条Track任意一条有数据, 则为Valid
bool TransformTrack::IsValid() 
{
	return mPosition.Size() > 1 || mRotation.Size() > 1 || mScale.Size() > 1;
}

// 选择三个Track里各种出现关键帧的最早的时间点, 三个再取最小的
float TransformTrack::GetStartTime() 
{
	float result = 0.0f;
	bool isSet = false;

	if (mPosition.Size() > 1) 
	{
		result = mPosition.GetStartTime();
		isSet = true;
	}
	if (mRotation.Size() > 1) 
	{
		float rotationStart = mRotation.GetStartTime();
		if (rotationStart < result || !isSet) 
		{
			result = rotationStart;
			isSet = true;
		}
	}
	if (mScale.Size() > 1) 
	{
		float scaleStart = mScale.GetStartTime();
		if (scaleStart < result || !isSet) 
		{
			result = scaleStart;
			isSet = true;
		}
	}

	return result;
}

// 取三个Track的EndTime里的最晚的
float TransformTrack::GetEndTime() 
{
	float result = 0.0f;
	bool isSet = false;

	if (mPosition.Size() > 1) 
	{
		result = mPosition.GetEndTime();
		isSet = true;
	}
	if (mRotation.Size() > 1) 
	{
		float rotationEnd = mRotation.GetEndTime();
		if (rotationEnd > result || !isSet) 
		{
			result = rotationEnd;
			isSet = true;
		}
	}
	if (mScale.Size() > 1) 
	{
		float scaleEnd = mScale.GetEndTime();
		if (scaleEnd > result || !isSet) 
		{
			result = scaleEnd;
			isSet = true;
		}
	}

	return result;
}

// 各个Track的Sample, 如果有Track的话
// 由于不是所有的动画都有相同的Property对应的track, 比如说有的只有position, 没有rotation和scale
// 在Sample动画A时，如果要换为Sample动画B，要记得重置人物的pose
Transform TransformTrack::Sample(const Transform& ref, float time, bool looping) 
{
	// 每次Sample来播放动画时, 都要记录好这个result数据
	Transform result = ref; // Assign default values

	// 这样的ref, 代表原本角色的Transform, 这样即使对应的Track没动画数据, 也没关系
	if (mPosition.Size() > 1) 
	{ // Only assign if animated
		result.position = mPosition.Sample(time, looping);
	}
	if (mRotation.Size() > 1) 
	{ // Only assign if animated
		result.rotation = mRotation.Sample(time, looping);
	}
	if (mScale.Size() > 1) 
	{ // Only assign if animated
		result.scale = mScale.Sample(time, looping);
	}
	
	return result;
}

Because not all animations contain the same tracks, it’s important to reset the pose that you are sampling any time the
animation that you are sampling switches. This ensures that the reference transform is always correct. To reset the pose, assign it to be the same as the rest pose

本章总结

这章学习了动画的本质，动画的本质就是一堆Track，或者说一堆Property的Curves，Track由一个Property的多个关键帧数据组成。后面的AnimationClips基本就是这章建立的TransformTrack对象的集合，Github上的Sample00带了此课的代码，Sample01把一些Track绘制了出来，因为预览这些Track的Curve对于Debug也是很有帮助的。

附录

fbx与glTF文件的区别

https://www.threekit.com/blog/gltf-vs-fbx-which-format-should-i-use

Difference between Spline, B-Spline and Bezier Curves

参考：https://www.geeksforgeeks.org/difference-between-spline-b-spline-and-bezier-curves/

没写完，以后再研究吧

Spline
Spline Curve是一个数学的表达方法，用于表示复杂的Curve和表面，我理解的是，这个东西就类似于
A spline curve is a mathematical representation for which it is easy to build an interface that will allow a user to design and control the shape of complex curves and surfaces.

B-Spline
B-Spline is a basis function that contains a set of control points. The B-Spline curves are specified by Bernstein basis function that has limited flexibility.

Attention reader! Don’t stop learning now. Get hold of all the important CS Theory concepts for SDE interviews with the CS Theory Course at a student-friendly price and become industry ready.

Bezier
These curves are specified with boundary conditions, with a characterizing matrix or with blending function. A Bezier curve section can be filled by any number of control points. The number of control points to be approximated and their relative position determine the degree of Bezier polynomial.