1.运算符的应用I
输入一个五位的整数i,依次将其个位,十位,百位,千位,万位数取出来保存到变量a,b,c,d,e中;按照输出案例的格式依次输出 c,d,b,e,a.
输入
五位整数
输出
取个位a,十位b,百位c,千位d,万位数e, 按照格式依次输出 c,d,b,e,a.
样例输入
12345
样例输出
32415
#include<stdio.h>
int main()
{
int x,a,b,c,d,e;
scanf("%d",&x);
a=x%10;
b=x/10%10;
c=x/100%10;
d=x/1000%10;
e=x/10000;
printf("%d%d%d%d%d",c,d,b,e,a);
return 0;
}
2.运算符的应用II
输入4个整数a,b,c,d;如果它们构成递增数列(所有相邻的元素满足<=关系),则输出1;否则输出0
样例输入
1 1 1 2
样例输出
1
#include<stdio.h>
int main()
{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
if(a<=b)
if(b<=c)
if(c<=d)
printf("1");
else
printf("0");
else
printf("0");
else
printf("0");
return 0;
}
#include<stdio.h>
int main()
{
int a,b,c,d,x;
int f=1,e=0;
scanf("%d%d%d%d",&a,&b,&c,&d);
x=b>=a?(c>=b?(d>=c?f:e):e):e;
printf("%d",x);
}
3.运算符的应用III
输入4个整数a,b,c,d;分别表示两个分数的分子和分母 (A=a/b ; B=c/d) ;按照小学数学中的计算算法(step 1.通分统一分母为两个分数的分母的积; step 2: 分子相加),计算并按照指定输出分数A和B的和(不需要约分)
样例输入
1 2 3 4
样例输出
10/8
#include<stdio.h>
int main()
{
int a,b,c,d,x,y;
scanf("%d%d%d%d",&a,&b,&c,&d);
y=b*d;
x=a*d+c*b;
printf("%d/%d",x,y);
return 1;
}
4.运算符的应用IV
如果一个4位的整数n的个位a,十位b,百位c,千位d的4次方的和等于该四位数( 即在数学上,n = a4 +b4 +c4 +d4),则称为整数n为 4叶水仙花数,输入一个 4位整数n,如果n是4叶水仙花数,则输出1;否则输出0
样例输入
1634
样例输出
1
#include<stdio.h>
#include<math.h>
int main()
{
int a,b,c,d,n,x;
scanf("%d",&n);
a=n%10;
b=n/10%10;
c=n/100%10;
d=n/1000;
x=pow(a,4)+pow(b,4)+pow(c,4)+pow(d,4);
if(n!=x)
printf("0");
else
printf("1");
return 1;
}
5.计算Relu函数
ReLu函数广泛应用于人工神经网络的激活函数。解决了Sigmoid激活函数的梯度消失的问题,推进了深度学习的发展。 然而,Relu函数是一个非常简单的分段函数:f(x) = x,如果x大于零,否则f(x) = 0,请编写程序,实现Relu函数。 输出保留到小数点后2位
输入
输入一个float类型数值x
输出
x小于零,输出0.00;否则保留2位小数输出x
样例输入
-3.2
样例输出
0.00
#include<stdio.h>
int main ()
{
float x;
scanf("%f",&x);
if(x<=0)
{
printf("0.00");
}else{
printf("%.2f",x);
}
return 0;
}
6.圆柱体
编写程序,输入底圆的半径r, 圆柱体的高h,求解并输出底圆的面积s及周长c,和圆柱体的体积v
(保留2位小数输出,具体格式见样例 PI=3.1416 )
输入
float 类型的r 和 h
输出
float类型的s,c, v
样例输入
2 3
样例输出
s=12.57
c=12.57
v=37.70
#include<stdio.h>
#define PI 3.1416
int main ()
{
float r,h,s,c,v;
scanf("%f %f",&r,&h);
s=PI*r*r;
c=PI*2*r;
v=PI*r*r*h;
printf("s=%.2f\nc=%.2f\nv=%.2f",s,c,v);
}
7.数学函数求解
编写程序求解以下数学函数,f(x) = max{ min{ 5x^2, 16x } ,(x mod 4) * 6 } , 其中x为整数
输入
整数x
输出
输出f(x)
样例输入
1
样例输出
6
提示
1.注意c语言表述与数学表述的区别!
2.mod表示求模,即求余数运算;x^y 表示x的y次幂
#include<stdio.h>
#define max(a,b) (a>b?a:b)
#define min(a1,b1) (a1>b1?b1:a1)
#include<math.h>
int main()
{
int a,b,a1,b1,c,d,x,e;
scanf("%d",&x);
d=(x%4)*6;
a1=5*pow(x,2);
b1=x*16;
c=min(a1,b1);
e=max(c,d);
printf("%d",e);
return 0;
}
8.一元二次方程
编写程序,输入二次项系数a,一次项系数b,常数项c;编写程序求解并输出axx + b*x + c = 0的两个根 (保留2位小数输出,具体格式见样例)
输入
float类型的a,b,c
输出
float类型的x1,x2
样例输入
1 -5 6
样例输出
x1=3.00
x2=2.00
#include<stdio.h>
#include<math.h>
void main()
{
float a,b,c,disc,x1,x2,p,q;
scanf("%f%f%f",&a,&b,&c);
disc=b*b-4*a*c;
p=-b/(2*a);
q=sqrt(disc)/(2*a);
x1=p+q;
x2=p-q;
printf("x1=%.2f\nx2=%.2f",x1,x2);
}
9.一元二次方程V2
编写程序,输入二次项系数a,一次项系数b,常数项c;输出axx + b*x + c = 0的两个根 (格式同 problem 1403), 如果有实数根;否则输出“no result”
样例输入
2 -5 6
样例输出
no result
#include<stdio.h>
#include<math.h>
void main()
{
float a,b,c,disc,x1,x2,p,q;
scanf("%f%f%f",&a,&b,&c);
disc=b*b-4*a*c;
p=-b/(2*a);
q=sqrt(disc)/(2*a);
x1=p+q;
x2=p-q;
if((b*b-4*a*c)<0)
printf("no result");
else
printf("x1=%.2f\nx2=%.2f",x1,x2);
}
10.简单判断
编写一个程序,在程序中从键盘输入三个整数,比较它们的大小,依次输出最小的数和最大的数
输入
输入a b c三个整数
输出
依次输出最小的数和最大的数,两个数用空格隔开
样例输入
222 44 33
样例输出
33 222
#include<stdio.h>
int main()
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
int t;
if(a<b)
{t=a;a=b;b=t;}
if(a<c)
{t=a;a=c;c=t;}
if(b<c){
printf("%d ",b);
printf("%d",a);
}else{
printf("%d",c);
printf("%d",a);
}
}
11.分段函数
求解下面分段函数
- 当 x <= -100:y=x;
- 当 -100 < x <=-10:y=x^2;
- 当 -10 < x < 0:y=x^3;
- 当 0 =< x < 10:y=x^4;
- 否则:y=0;
输入
整数x
输出
整数y
样例输入
-100
样例输出
-100
提示
此处x^2, x^3, x^4 分别代表x的2次方,3次方,4次方
#include<stdio.h>
int main()
{
int x,y;
scanf("%d",&x);
if(x<=-100)
y=x;
else if(x>-100&&x<=-10)
y=x*x;
else if(x>-10&&x<0)
y=x*x*x;
else if(x>=0&&x<10)
y=x*x*x*x;
else
y=0;
printf("%d",y);
}
12.Dancing number判定 V1
我们称n位整数 X = x_{n}x_{n-1}x_{n-2}…x_{2}x_{1} 是一个dancing number,如果X的第i位数x_{i} 同时大于 x_{i-1}和 x_{i+1} 或者 同时小于 x_{i-1}和 x_{i+1} , 其中 i 属于 {2,3,…, n-2, n-1 }
即满足以下两个条件之一:
- x_{1} < x_{2} 并且 x_{2} > x_{3} 并且 x_{3} < x_{4} 并且 x_{4} > x_{5}…
- x_{1} > x_{2} 并且 x_{2} < x_{3} 并且 x_{3} > x_{4} 并且 x_{4} < x_{5}…
编写程序判断输入的正整数是否为 5位 dancing number.
输入
整数x
输出
如果x不是5位正整数,输出"input error"; 如果 x是 5位dancing number,输出"yes" ;否则输出"no"
样例输入
12143
样例输出
yes
#include<stdio.h>
int main()
{
int a,b,c,d,e,f,g;
int i;
scanf("%d",&a);
b=a;
for(i=0;b>=1;i++)
{b=b/10;}
g=a%10;
f=a/10%10;
e=a/100%10;
d=a/1000%10;
c=a/10000;
if(i==5){
if(d>c&&d>e&&f>e&&f>g)
printf("yes");
else if(d<c&&d<e&&f<e&&f<g)
printf("yes");
else
printf("no");
}else{
printf("input error");
}
}
13.Dancing Number的判定 V2
输入一个正整数 n (100 =< n <= 200000000), 输出是否为dancing number,及n的位数
输入
输入一个正整数 n
输出
输出是否为dancing number,及n的位数(输出格式为:0或1,位数 其中0表示n不是dancing number,1表示n是dancing number),如果100 =< n <= 200000000;否则输出“error input”
样例输入
123456
样例输出
0,6
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main()
{
int k = 0;
int n,i,a,b,c,n1;
int arr[20] = {0};
scanf("%d",&n);
n1 = n;
while(n != 0)
{
n=n/10;
k++;
}
n = n1;
for(i=0;i<=k-1;i++)
{
a=n%10;
arr[i] = a;
n = n/10;
}
n = n1;
if(n>=100 && n<=2*pow(10,8))
{
if(k%2 == 1)
{
for(a=0,b=1,c=2;c<=k-1;a+=2,b+=2,c+=2)
{
if(arr[b]>arr[a] && arr[b]>arr[c])
{
continue;
}
else
{
goto wocao;
}
}
printf("1,");
printf("%d",k);
exit(0);
}
else
{
for(a=0,b=1,c=2;b<=k-1;a+=2,b+=2,c+=2)
{
if(arr[b]>arr[a] && arr[b]>arr[c])
{
continue;
}
else
{
goto wocao;
}
}
printf("1,");
printf("%d",k);
exit(0);
}
}
else
{
printf("error input");
exit(0);
}
wocao:
if(k%2 == 1)
{
for(a=0,b=1,c=2;arr[b]<arr[a] && arr[b]<arr[c];a+=2,b+=2,c+=2)
{
continue;
}
if(c == k-1)
{
printf("1,");
}
else
{
printf("0,");
}
}
else
{
for(a=0,b=1,c=2;arr[b]<arr[a] && arr[b]<arr[c];a+=2,b+=2,c+=2)
{
continue;
}
if(b == k-1)
{
printf("1,");
}
else
{
printf("0,");
}
}
printf("%d",k);
return 0;
}
#include<stdio.h>
#include<math.h>
int main()
{
int n, h = 0, t = 0, j, a[9], f = 0, x = 0, y = 0;
scanf_s("%d", &n);
if (n>=100 && n<=200000000)
{
h = n;
while (h != 0)
{
h/=10;t++;
}
for(j=0;j<t;j++)
{
f=(int)pow(10, j);
a[j]=n/f%10;
}
if(t%2)
{
for(j=1;j<=(t-1)/2;j++)
{
if(a[2*j-2]<a[2*j-1] && a[2*j-1]>a[2*j])
x++;
else if(a[2*j-2]>a[2*j-1] && a[2*j-1]<a[2*j])
y++;
else
break;
}
}
else
{
for(j=1;j<=t/2;j++)
{
if(j<t/2)
{
if(a[2*j-2]<a[2*j-1] && a[2*j-1]>a[2*j])
x++;
else if(a[2*j-2]>a[2*j-1] && a[2*j-1]<a[2*j])
y++;
}
else if(j == t / 2)
{
if(a[2*j-2]<a[2*j-1])
x++;
else if(a[2*j-2]>a[2*j-1])
y++;
}
else
break;
}
}
if(t%2 == 1)
{
if(x==(t - 1)/2 || y==t/2)
printf("%d,%d",1,t);
else
printf("%d,%d",0,t);
}
else if(t%2 == 0)
{
if(x==t/2 || y==t/2)
printf("%d,%d",1,t);
else
printf("%d,%d",0,t);
}
}
else
printf("error input");
return 0;
}
14.简单循环求和
编写一个程序,输入一个整数n(1 <= n <= 1000),如果n是奇数, 输出 1+3+5+...+n的值。如果n是偶数,则输出2 + 4 + … + n
输入
输入整数n
输出
n不满足1 <= n <= 1000,则输出error input
n为奇数,则输出1+3+…+n
n为偶数,则输出2+4…+n
样例输入
10
样例输出
30
#include<stdio.h>
int main()
{
int a,b,c;
scanf("%d",&a);
b=(1+a)*((a+1)/2)*0.5;
c=(2+a)*(a/2)*0.5;
if(1<=a&&a<=1000)
if(a%2==1)
printf("%d",b);
else
printf("%d",c);
else
printf("error input");
}
15. 级数运算I
输入正整数n,求12+23+34+…n(n+1)
样例输入
3
样例输出
20
#include <stdio.h>
void main()
{
int a,b,n,sum=0;
scanf("%d",&n);
for(a=1,b=2;a<=n;a++,b++)
sum=a*b+sum;
printf("%d",sum);
}
16.级数运算II
输入正整数n,输出满足1+2+3+…+i <= n 的最大的i
样例输入
8
样例输出
3
#include <stdio.h>
int main()
{
int a,n,sum=0;
scanf("%d",&n);
for(a=1;;a++)
{
sum=sum+a;
if(sum>n)
{
printf("%d",a-1);
break;
}
}
return 0;
}
17.级数运算III
输入一个正整数 n(1 =< n <= 10), 求级数 1/1! - 1/2! + 1/3! - … (-1)^{n+1}/n!的值,(采用double类型,保留8位小数)。
输入
一个正整数 n(1 =< n <= 10)
输出
1/1! - 1/2! + 1/3! - … (-1)^{n+1}/n!的值,当n满足要求;否则输出"error input"
样例输入
5
样例输出
0.63333333
#include <stdio.h>
#include<math.h>
int main()
{
int a,n,sum=1;
double b=0;
scanf("%d",&n);
if(n>=1 && n<=10){
for(a=1;a<=n;a++){
sum=sum*a;
b=b+pow(-1,a-1)/sum;}
printf("%.8f",b);}
else
printf("error input");
return 0;
}
18.级数运算V
按照以下公式求圆周率pi,运算到最后一个乘法项 小于 k = 1 + 1e-10 ( 即 k = 1.0000000001)为止。
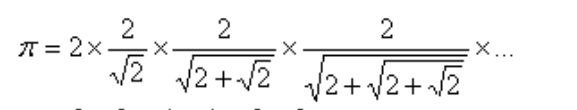
输出每次迭代的结果。 要求采用double类型表示和计算pi
按照以下方式:
printf("%-3d: item=%-15.10lf; pi=%-15.10lf\n",k,item,pi);//k是迭代次数(首次迭代输出1),item为乘项(首个累乘项为2/sqrt(2)),pi为当前累乘值
例如,第一行输出:
1 : item=1.4142135624 ; pi=2.8284271247
#include <stdio.h>
#include<math.h>
int main()
{
double pi,item;
int k;
for(pi=2,k=1,item=sqrt(2);;k++)
{
pi=pi*2/item;
printf("%-3d: item=%-15.10lf; pi=%-15.10lf\n",k,2/item,pi);
item=sqrt(2+item);
if(2/item<(1+1e-10))
break;
}
return 0;
}
19.星钻图形输出V2
输入一个正整数 n(n>=1),从以下范例中寻找规律,输出 (2*n-1) 行符号:

#include<stdio.h>
int main()
{
int n = 0, a,b,c,d,e=0;
scanf("%d", &n);
for (a=1;a<=n;a++)
{
for(b=a;b<=n-1;b++)
{
printf(" ");
}
for(c=1;c<=2*a-1;c++)
{
printf("*");
}
printf("\n");
}
for(a=n+1;a<=2*n-1;a++)
{
for(b=1;b<=a-n;b++)
{
printf(" ");
}
e++;
for(d=1;d<=(c-1)-2*e;d++)
{
printf("*");
}
printf("\n");
}
return 0;
}
20.求不大于n的所有素数的和
输入一个正整数 n(10 =< n <= 10000), 求不大于n的所有素数的和
输入
输入一个正整数 n(10 =< n <= 10000)
输出
输出不大于n的所有素数的和,如果10 =< n <= 10000;否则,输出"error input"
样例输入
20
样例输出
77
#include<stdio.h>
int main()
{
int n = 0,i = 0,sum = 0,j = 0;;
scanf("%d",&n);
if(n>=10 && n<=10000)
{
for(i=5;i<=n;i+=2)
{
for(j=3;j<i;j++)
{
if(i%j == 0)
{
break;
}
}
if(j == i)
{
sum=sum+i;
}
}
printf("%d",sum+5);
}
else
{
printf("error input");
}
return 0;
}
21.N叶水仙花数
设 n位正整数 k 的第 i (1<=i<=n) 位数为:ki; 如果满足 k = k1^n + k2^n +…+ knn(kin为数学表示,即表示ki的n次方), 则称 k为 n叶水仙花数。 输入一个正整数 m (1 =< m <= 9),从小到大输出所有的1叶水仙花数, 2叶水仙花数, …, m叶水仙花数
输入
正整数m
输出
输出所有的1叶水仙花数, 2叶水仙花数, …, m叶水仙花数,如果1 =< m <= 9;否则输出“error input”
样例输入
4
样例输出
1
2
3
4
5
6
7
8
9
153
370
371
407
1634
8208
9474
#include<stdio.h>
int Pow(int x,int y)
{
int z,result = 1;
for(z=1;z<=y;z++)
{
result=result*x;
}
return result;
}
int main()
{
int a,b,k,n = 0,sum = 0,a1;
scanf("%d",&k);
if(k>=1 && k<=9)
{
for(a=1;a<=Pow(10,k);a++)
{
a1=a;
while(a != 0)
{
a=a/10;
n++;
}
a = a1;
while(a>0)
{
b=a%10;
sum=sum+Pow(b,n);
a=a/10;
}
a = a1;
if(sum == a)
{
printf("%d\n",sum);
}
n = 0;
sum = 0;
}
}
else
{
printf("error input");
}
return 0;
}